Nine-point stencil

Innumerical analysis,given asquare gridin two dimensions, thenine-point stencilof a point in the grid is astencilmade up of the point itself together with its eight "neighbors". It is used to writefinite differenceapproximations toderivativesat grid points. It is an example fornumerical differentiation.This stencil is often used to approximate theLaplacianof a function of two variables.

An illustration of the nine-point stencil in two dimensions.

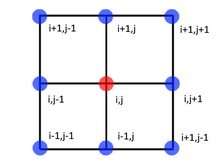
Motivation

If we discretize the 2DLaplacianby usingcentral-difference methods,we obtain the commonly usedfive-point stencil,represented by the followingconvolutionkernel:

$D_{CD}={\begin{bmatrix}0&1&0\\1&-4&1\\0&1&0\end{bmatrix}}$

Starting from homogeneous initial conditions with only one point-like perturbation, the correct growth process would yield a circle (left). If growth is faster along the coordinate axes, which is caused by the anisotropic effect of central difference discretization, the circle would turn into star-shaped structure, as the errors propagate (right):.

Even though it is simple to obtain and computationally lighter, the centraldifference kernelpossess an undesired intrinsicanisotropicproperty, since it doesn't take into account the diagonal neighbours. This intrinsic anisotropy poses a problem when applied on certain numerical simulations or when more accuracy is required, by propagating the Laplacian effect faster in thecoordinate axesdirections and slower in the other directions, thus distortiong the final result.

This drawback calls for finding better methods for discretizing the Laplacian, reducing or eliminating the anisotropy.

Implementation

The two most commonly usedisotropicnine-point stencils are displayed below, in their convolution kernel forms. They can be obtained by the following formula:

$D=(1-\gamma ){\begin{bmatrix}0&1&0\\1&-4&1\\0&1&0\end{bmatrix}}+\gamma {\begin{bmatrix}1/2&0&1/2\\0&-2&0\\1/2&0&1/2\end{bmatrix}}$

The first one is known by Oono-Puri,and it is obtained when γ=1/2.

$D_{OP}={\begin{bmatrix}1/4&2/4&1/4\\2/4&-12/4&2/4\\1/4&2/4&1/4\end{bmatrix}}={\begin{bmatrix}0.25&0.5&0.25\\0.5&-3&0.5\\0.25&0.5&0.25\end{bmatrix}}$

The second one is known by Patra-Karttunen or Mehrstellen,and it is obtained when γ=1/3.

$D_{PK}={\begin{bmatrix}1/6&4/6&1/6\\4/6&-20/6&4/6\\1/6&4/6&1/6\end{bmatrix}}={\begin{bmatrix}0.16&0.66&0.16\\0.66&-3.33&0.66\\0.16&0.66&0.16\end{bmatrix}}$

Both are isotropic forms ofdiscrete Laplacian,and in the limit of small Δx, they all become equivalent,as Oono-Puri being described as the optimally isotropic form of discretization,displaying reduced overall error,and Patra-Karttunen having been systematically derived by imposing conditions of rotational invariance,displaying smallest error around the origin.

Desired anisotropy

On the other hand, if controlledanisotropiceffects are a desired feature, when solvinganisotropic diffusionproblems for example, it is also possible to use the 9-point stencil combined withtensorsto generate them.

Consider the laplacian in the following form:

$c\nabla ^{2}A=cD_{OP}*A$

Where c is just a constant coefficient. Now if we replace c by the2nd rank tensorC:

$C={\begin{bmatrix}c_{1}&0\\0&c_{2}\end{bmatrix}}$

Where c1 is the constant coefficient for the principal direction in x axis, and c2 is the constant coefficient for the secondary direction in y axis. In order to generate anisotropic effects, c1 and c2 must be different.

By multiplying it by therotation matrixQ, we obtain C', allowing anisotropic propagations in arbitrary directions other than thecoordinate axes.

$Q={\begin{bmatrix}\cos \theta &\sin \theta \\-\sin \theta &\cos \theta \end{bmatrix}}$

$C'=QCQ^{\operatorname {T} }$

$C'={\begin{bmatrix}c_{xx}&c_{xy}\\c_{xy}&c_{yy}\end{bmatrix}}={\begin{bmatrix}c_{1}\cos ^{2}\theta +c_{2}\sin ^{2}\theta &(c_{2}-c_{1})\cos \theta \sin \theta \\(c_{2}-c_{1})\cos \theta \sin \theta &c_{2}\cos ^{2}\theta +c_{1}\sin ^{2}\theta \end{bmatrix}}$

Which is very similar to theCauchy stress tensorin 2 dimensions. The angle$\theta$can be obtained by generating avector field$\mathbf {V} =V_{x}{\mathbf {i} }+V_{y}{\mathbf {j} }$in order to orientate the pattern as desired.Then:

$\theta =\arctan(V_{y}/V_{x})$

Or, for different anisotropic effects using the same vector field

$\theta =\arctan(V_{y}/-V_{x})$

It is important to note that, regardless of the values of$\theta$,the anisotropic propagation will occur parallel to the secondary direction c2 and perpendicular to the principal direction c1:.The resulting convolution kernel is as follows

$D_{Aniso}={\begin{bmatrix}{\frac {-c_{xy}}{2}}&c_{yy}&{\frac {c_{xy}}{2}}\\c_{xx}&-2(c_{xx}+c_{yy})&c_{xx}\\{\frac {c_{xy}}{2}}&c_{yy}&{\frac {-c_{xy}}{2}}\end{bmatrix}}$

If, for example, c1=c2=1, the cxy component will vanish, resulting in the simplefive-point stencil,rendering no controlled anisotropy.

If c2>c1 and$\theta$=0, the anisotropic effects will be more pronounced in the vertical axis.

if c2>c1 and$\theta$=45 degrees, the anisotropic effects will be more pronounced in the upper-right / lower-left diagonal.