Nonlinear system

This article is about "nonlinearity" in mathematics, physics and other sciences. For video and film editing, seeNon-linear editing system.For other uses, seeNonlinearity (disambiguation)."Nonlinear dynamics" redirects here. For the journal, seeNonlinear Dynamics (journal).

Inmathematicsandscience,anonlinear system(or anon-linear system) is asystemin which the change of the output is notproportionalto the change of the input.Nonlinear problems are of interest toengineers,biologists,physicists,mathematicians,and many otherscientistssince most systems are inherently nonlinear in nature.Nonlineardynamical systems,describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simplerlinear systems.

Typically, the behavior of a nonlinear system is described in mathematics by anonlinear system of equations,which is a set of simultaneousequationsin which the unknowns (or the unknown functions in the case ofdifferential equations) appear as variables of apolynomialof degree higher than one or in the argument of afunctionwhich is not a polynomial of degree one. In other words, in a nonlinear system of equations, the equation(s) to be solved cannot be written as alinear combinationof the unknownvariablesorfunctionsthat appear in them. Systems can be defined as nonlinear, regardless of whether known linear functions appear in the equations. In particular, a differential equation islinearif it is linear in terms of the unknown function and its derivatives, even if nonlinear in terms of the other variables appearing in it.

As nonlinear dynamical equations are difficult to solve, nonlinear systems are commonly approximated by linear equations (linearization). This works well up to some accuracy and some range for the input values, but some interesting phenomena such assolitons,chaos,andsingularitiesare hidden by linearization. It follows that some aspects of the dynamic behavior of a nonlinear system can appear to be counterintuitive, unpredictable or even chaotic. Although such chaotic behavior may resemblerandombehavior, it is in fact not random. For example, some aspects of the weather are seen to be chaotic, where simple changes in one part of the system produce complex effects throughout. This nonlinearity is one of the reasons why accurate long-term forecasts are impossible with current technology.

Some authors use the termnonlinear sciencefor the study of nonlinear systems. This term is disputed by others:

Using a term like nonlinear science is like referring to the bulk of zoology as the study of non-elephant animals.

— Stanisław Ulam

Definition

Inmathematics,alinear map(orlinear function)$f(x)$is one which satisfies both of the following properties:

• Additivity orsuperposition principle:$\textstyle f(x+y)=f(x)+f(y);$
• Homogeneity:$\textstyle f(\ Alpha x)=\ Alpha f(x).$

Additivity implies homogeneity for anyrationalα,and, forcontinuous functions,for anyrealα.For acomplexα,homogeneity does not follow from additivity. For example, anantilinear mapis additive but not homogeneous. The conditions of additivity and homogeneity are often combined in the superposition principle

$f(\ Alpha x+\beta y)=\ Alpha f(x)+\beta f(y)$

An equation written as

$f(x)=C$

is calledlinearif$f(x)$is a linear map (as defined above) andnonlinearotherwise. The equation is calledhomogeneousif$C=0$and$f(x)$is ahomogeneous function.

The definition$f(x)=C$is very general in that$x$can be any sensible mathematical object (number, vector, function, etc.), and the function$f(x)$can literally be anymapping,including integration or differentiation with associated constraints (such asboundary values). If$f(x)$containsdifferentiationwith respect to$x$,the result will be adifferential equation.

Nonlinear systems equations

A nonlinear system of equations consists of a set of equations in several variables such that at least one of them is not alinear equation.

For a single equation of the form$f(x)=0,$many methods have been designed; seeRoot-finding algorithm.In the case wherefis apolynomial,one has apolynomial equationsuch as $x^{2}+x-1=0.$The general root-finding algorithms apply to polynomial roots, but, generally they do not find all the roots, and when they fail to find a root, this does not imply that there is no roots. Specific methods for polynomials allow finding all roots or therealroots; seereal-root isolation.

Solvingsystems of polynomial equations,that is finding the common zeros of a set of several polynomials in several variables is a difficult problem for which elaborated algorithms have been designed, such asGröbner basealgorithms.

For the general case of system of equations formed by equating to zero severaldifferentiable functions,the main method isNewton's methodand its variants. Generally they may provide a solution, but do not provide any information on the number of solutions.

Nonlinear recurrence relations

A nonlinearrecurrence relationdefines successive terms of asequenceas a nonlinear function of preceding terms. Examples of nonlinear recurrence relations are thelogistic mapand the relations that define the variousHofstadter sequences.Nonlinear discrete models that represent a wide class of nonlinear recurrence relationships include the NARMAX (Nonlinear Autoregressive Moving Average with eXogenous inputs) model and the relatednonlinear system identificationand analysis procedures.These approaches can be used to study a wide class of complex nonlinear behaviors in the time, frequency, and spatio-temporal domains.

Nonlinear differential equations

Asystemofdifferential equationsis said to be nonlinear if it is not asystem of linear equations.Problems involving nonlinear differential equations are extremely diverse, and methods of solution or analysis are problem dependent. Examples of nonlinear differential equations are theNavier–Stokes equationsin fluid dynamics and theLotka–Volterra equationsin biology.

One of the greatest difficulties of nonlinear problems is that it is not generally possible to combine known solutions into new solutions. In linear problems, for example, a family oflinearly independentsolutions can be used to construct general solutions through thesuperposition principle.A good example of this is one-dimensional heat transport withDirichlet boundary conditions,the solution of which can be written as a time-dependent linear combination of sinusoids of differing frequencies; this makes solutions very flexible. It is often possible to find several very specific solutions to nonlinear equations, however the lack of a superposition principle prevents the construction of new solutions.

Ordinary differential equations

First orderordinary differential equationsare often exactly solvable byseparation of variables,especially for autonomous equations. For example, the nonlinear equation

${\frac {du}{dx}}=-u^{2}$

has$u={\frac {1}{x+C}}$as a general solution (and also the special solution$u=0,$corresponding to the limit of the general solution whenCtends to infinity). The equation is nonlinear because it may be written as

${\frac {du}{dx}}+u^{2}=0$

and the left-hand side of the equation is not a linear function of$u$and its derivatives. Note that if the$u^{2}$term were replaced with$u$,the problem would be linear (theexponential decayproblem).

Second and higher order ordinary differential equations (more generally, systems of nonlinear equations) rarely yieldclosed-formsolutions, though implicit solutions and solutions involvingnonelementary integralsare encountered.

Common methods for the qualitative analysis of nonlinear ordinary differential equations include:

• Examination of anyconserved quantities,especially inHamiltonian systems
• Examination of dissipative quantities (seeLyapunov function) analogous to conserved quantities
• Linearization viaTaylor expansion
• Change of variables into something easier to study
• Bifurcation theory
• Perturbationmethods (can be applied to algebraic equations too)
• Existence of solutions of Finite-Duration,which can happen under specific conditions for some non-linear ordinary differential equations.

Partial differential equations

Main article:Nonlinear partial differential equation

See also:List of nonlinear partial differential equations

The most common basic approach to studying nonlinearpartial differential equationsis to change the variables (or otherwise transform the problem) so that the resulting problem is simpler (possibly linear). Sometimes, the equation may be transformed into one or moreordinary differential equations,as seen inseparation of variables,which is always useful whether or not the resulting ordinary differential equation(s) is solvable.

Another common (though less mathematical) tactic, often exploited in fluid and heat mechanics, is to usescale analysisto simplify a general, natural equation in a certain specificboundary value problem.For example, the (very) nonlinearNavier-Stokes equationscan be simplified into one linear partial differential equation in the case of transient, laminar, one dimensional flow in a circular pipe; the scale analysis provides conditions under which the flow is laminar and one dimensional and also yields the simplified equation.

Other methods include examining thecharacteristicsand using the methods outlined above for ordinary differential equations.

Pendula

Main article:Pendulum (mathematics)

Illustration of a pendulum

Linearizations of a pendulum

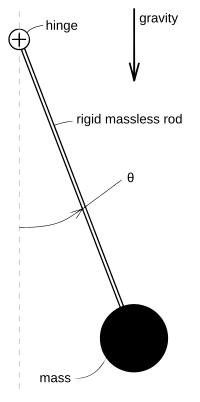
A classic, extensively studied nonlinear problem is the dynamics of a frictionlesspendulumunder the influence ofgravity.UsingLagrangian mechanics,it may be shownthat the motion of a pendulum can be described by thedimensionlessnonlinear equation

${\frac {d^{2}\theta }{dt^{2}}}+\sin(\theta )=0$

where gravity points "downwards" and$\theta$is the angle the pendulum forms with its rest position, as shown in the figure at right. One approach to "solving" this equation is to use$d\theta /dt$as anintegrating factor,which would eventually yield

$\int {\frac {d\theta }{\sqrt {C_{0}+2\cos(\theta )}}}=t+C_{1}$

which is an implicit solution involving anelliptic integral.This "solution" generally does not have many uses because most of the nature of the solution is hidden in thenonelementary integral(nonelementary unless$C_{0}=2$).

Another way to approach the problem is to linearize any nonlinearity (the sine function term in this case) at the various points of interest throughTaylor expansions.For example, the linearization at$\theta =0$,called the small angle approximation, is

${\frac {d^{2}\theta }{dt^{2}}}+\theta =0$

since$\sin(\theta )\approx \theta$for$\theta \approx 0$.This is asimple harmonic oscillatorcorresponding to oscillations of the pendulum near the bottom of its path. Another linearization would be at$\theta =\pi$,corresponding to the pendulum being straight up:

${\frac {d^{2}\theta }{dt^{2}}}+\pi -\theta =0$

since$\sin(\theta )\approx \pi -\theta$for$\theta \approx \pi$.The solution to this problem involveshyperbolic sinusoids,and note that unlike the small angle approximation, this approximation is unstable, meaning that$|\theta |$will usually grow without limit, though bounded solutions are possible. This corresponds to the difficulty of balancing a pendulum upright, it is literally an unstable state.

One more interesting linearization is possible around$\theta =\pi /2$,around which$\sin(\theta )\approx 1$:

${\frac {d^{2}\theta }{dt^{2}}}+1=0.$

This corresponds to a free fall problem. A very useful qualitative picture of the pendulum's dynamics may be obtained by piecing together such linearizations, as seen in the figure at right. Other techniques may be used to find (exact)phase portraitsand approximate periods.

Types of nonlinear dynamic behaviors

• Amplitude death– any oscillations present in the system cease due to some kind of interaction with other system or feedback by the same system
• Chaos– values of a system cannot be predicted indefinitely far into the future, and fluctuations areaperiodic
• Multistability– the presence of two or more stable states
• Solitons– self-reinforcing solitary waves
• Limit cycles– asymptotic periodic orbits to which destabilized fixed points are attracted.
• Self-oscillations– feedback oscillations taking place in open dissipative physical systems.

Examples of nonlinear equations

• Algebraic Riccati equation
• Ball and beamsystem
• Bellman equationfor optimal policy
• Boltzmann equation
• Colebrook equation
• General relativity
• Ginzburg–Landau theory
• Ishimori equation
• Kadomtsev–Petviashvili equation
• Korteweg–de Vries equation
• Landau–Lifshitz–Gilbert equation
• Liénard equation
• Navier–Stokes equationsoffluid dynamics
• Nonlinear optics
• Nonlinear Schrödinger equation
• Power-flow study
• Richards equationfor unsaturated water flow
• Self-balancing unicycle
• Sine-Gordon equation
• Van der Pol oscillator
• Vlasov equation

See also

• Aleksandr Mikhailovich Lyapunov
• Dynamical system
• Feedback
• Initial condition
• Linear system
• Mode coupling
• Vector soliton
• Volterra series

Further reading

• Diederich Hinrichsenand Anthony J. Pritchard (2005).Mathematical Systems Theory I - Modelling, State Space Analysis, Stability and Robustness.Springer Verlag.ISBN9783540441250.
• Jordan, D. W.; Smith, P. (2007).Nonlinear Ordinary Differential Equations(fourth ed.). Oxford University Press.ISBN978-0-19-920824-1.
• Khalil, Hassan K. (2001).Nonlinear Systems.Prentice Hall.ISBN978-0-13-067389-3.
• Kreyszig, Erwin(1998).Advanced Engineering Mathematics.Wiley.ISBN978-0-471-15496-9.
• Sontag, Eduardo(1998).Mathematical Control Theory: Deterministic Finite Dimensional Systems. Second Edition.Springer.ISBN978-0-387-98489-6.

External links

• Command and Control Research Program (CCRP)
• New England Complex Systems Institute: Concepts in Complex Systems
• Nonlinear Dynamics I: ChaosatMIT's OpenCourseWare
• Nonlinear Model Library– (inMATLAB) a Database of Physical Systems
• The Center for Nonlinear Studies at Los Alamos National Laboratory