Orientability

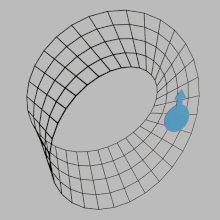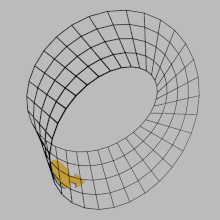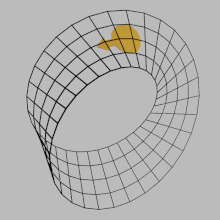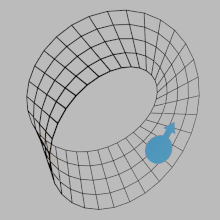
Inmathematics,orientabilityis a property of sometopological spacessuch asreal vector spaces,Euclidean spaces,surfaces,and more generallymanifoldsthat allows a consistent definition of "clockwise" and "anticlockwise".^[1]A space isorientableif such a consistent definition exists. In this case, there are two possible definitions, and a choice between them is anorientationof the space. Real vector spaces, Euclidean spaces, andspheresare orientable. A space isnon-orientableif "clockwise" is changed into "counterclockwise" after running through someloopsin it, and coming back to the starting point. This means that ageometric shape,such as,that moves continuously along such a loop is changed into its ownmirror image.AMöbius stripis an example of a non-orientable space.

Various equivalent formulations of orientability can be given, depending on the desired application and level of generality. Formulations applicable to general topological manifolds often employ methods ofhomology theory,whereas fordifferentiable manifoldsmore structure is present, allowing a formulation in terms ofdifferential forms.A generalization of the notion of orientability of a space is that of orientability of a family of spaces parameterized by some other space (afiber bundle) for which an orientation must be selected in each of the spaces which varies continuously with respect to changes in the parameter values.

Orientable surfaces

A surfaceSin theEuclidean spaceR³isorientableif achiraltwo-dimensional figure (for example,) cannot be moved around the surface and back to where it started so that it looks like its own mirror image (). Otherwise the surface isnon-orientable.An abstract surface (i.e., a two-dimensionalmanifold) is orientable if a consistent concept of clockwise rotation can be defined on the surface in a continuous manner. That is to say that a loop going around one way on the surface can never be continuously deformed (without overlapping itself) to a loop going around the opposite way. This turns out to be equivalent to the question of whether the surface contains no subset that ishomeomorphicto theMöbius strip.Thus, for surfaces, the Möbius strip may be considered the source of all non-orientability.

For an orientable surface, a consistent choice of "clockwise" (as opposed to counter-clockwise) is called anorientation,and the surface is calledoriented.For surfaces embedded in Euclidean space, an orientation is specified by the choice of a continuously varyingsurface normalnat every point. If such a normal exists at all, then there are always two ways to select it:nor −n.More generally, an orientable surface admits exactly two orientations, and the distinction between an orientedsurface and an orientablesurface is subtle and frequently blurred. An orientable surface is an abstract surface that admits an orientation, while an oriented surface is a surface that is abstractly orientable, and has the additional datum of a choice of one of the two possible orientations.

Examples

Most surfaces encountered in the physical world are orientable.Spheres,planes,andtoriare orientable, for example. ButMöbius strips,real projective planes,andKlein bottlesare non-orientable. They, as visualized in 3-dimensions, all have just one side. The real projective plane and Klein bottle cannot be embedded inR³,onlyimmersedwith nice intersections.

Note that locally an embedded surface always has two sides, so a near-sighted ant crawling on a one-sided surface would think there is an "other side". The essence of one-sidedness is that the ant can crawl from one side of the surface to the "other" without going through the surface or flipping over an edge, but simply by crawling far enough.

In general, the property of being orientable is not equivalent to being two-sided; however, this holds when the ambient space (such asR³above) is orientable. For example, a torus embedded in

K^{2}\times S^{1}

can be one-sided, and a Klein bottle in the same space can be two-sided; here $K^{2}$ refers to the Klein bottle.

Orientation by triangulation

Any surface has atriangulation:a decomposition into triangles such that each edge on a triangle is glued to at most one other edge. Each triangle is oriented by choosing a direction around the perimeter of the triangle, associating a direction to each edge of the triangle. If this is done in such a way that, when glued together, neighboring edges are pointing in the opposite direction, then this determines an orientation of the surface. Such a choice is only possible if the surface is orientable, and in this case there are exactly two different orientations.

If the figurecan be consistently positioned at all points of the surface without turning into its mirror image, then this will induce an orientation in the above sense on each of the triangles of the triangulation by selecting the direction of each of the triangles based on the order red-green-blue of colors of any of the figures in the interior of the triangle.

This approach generalizes to anyn-manifold having a triangulation. However, some 4-manifolds do not have a triangulation, and in general forn> 4 somen-manifolds have triangulations that are inequivalent.

Orientability and homology

IfH₁(S) denotes the firsthomologygroup of a closed surfaceS,thenSis orientable if and only ifH₁(S) has a trivialtorsion subgroup.More precisely, ifSis orientable thenH₁(S) is afree abelian group,and if not thenH₁(S) =F+Z/2ZwhereFis free abelian, and theZ/2Zfactor is generated by the middle curve in aMöbius bandembedded inS.

Orientability of manifolds

LetMbe a connected topologicaln-manifold.There are several possible definitions of what it means forMto be orientable. Some of these definitions require thatMhas extra structure, like being differentiable. Occasionally, $n = 0$ must be made into a special case. When more than one of these definitions applies toM,thenMis orientable under one definition if and only if it is orientable under the others.^[2]^[3]

Orientability of differentiable manifolds

The most intuitive definitions require thatMbe a differentiable manifold. This means that the transition functions in the atlas ofMareC¹-functions. Such a function admits aJacobian determinant.When the Jacobian determinant is positive, the transition function is said to beorientation preserving.Anoriented atlasonMis an atlas for which all transition functions are orientation preserving.Misorientableif it admits an oriented atlas. When $n > 0$ ,anorientationofMis a maximal oriented atlas. (When $n = 0$ ,an orientation ofMis a function $M \to {\pm1}$ .)

Orientability and orientations can also be expressed in terms of the tangent bundle. The tangent bundle is avector bundle,so it is afiber bundlewithstructure group $GL(n, R)$ .That is, the transition functions of the manifold induce transition functions on the tangent bundle which are fiberwise linear transformations. If the structure group can be reduced to the group $GL + (n, R)$ of positive determinant matrices, or equivalently if there exists an atlas whose transition functions determine an orientation preserving linear transformation on each tangent space, then the manifoldMis orientable. Conversely,Mis orientable if and only if the structure group of the tangent bundle can be reduced in this way. Similar observations can be made for the frame bundle.

Another way to define orientations on a differentiable manifold is throughvolume forms.A volume form is a nowhere vanishing sectionωof $⋀ n T * M$ ,the top exterior power of the cotangent bundle ofM.For example,Rⁿhas a standard volume form given by $dx 1 \land \dots \land dx n$ .Given a volume form onM,the collection of all charts $U \to R n$ for which the standard volume form pulls back to a positive multiple ofωis an oriented atlas. The existence of a volume form is therefore equivalent to orientability of the manifold.

Volume forms and tangent vectors can be combined to give yet another description of orientability. If $X 1,\dots, X n$ is a basis of tangent vectors at a pointp,then the basis is said to beright-handedif $ω(X 1,\dots, X n) > 0$ .A transition function is orientation preserving if and only if it sends right-handed bases to right-handed bases. The existence of a volume form implies a reduction of the structure group of the tangent bundle or the frame bundle to $GL + (n, R)$ .As before, this implies the orientability ofM.Conversely, ifMis orientable, then local volume forms can be patched together to create a global volume form, orientability being necessary to ensure that the global form is nowhere vanishing.

Homology and the orientability of general manifolds

At the heart of all the above definitions of orientability of a differentiable manifold is the notion of an orientation preserving transition function. This raises the question of what exactly such transition functions are preserving. They cannot be preserving an orientation of the manifold because an orientation of the manifold is an atlas, and it makes no sense to say that a transition function preserves or does not preserve an atlas of which it is a member.

This question can be resolved by defining local orientations. On a one-dimensional manifold, a local orientation around a pointpcorresponds to a choice of left and right near that point. On a two-dimensional manifold, it corresponds to a choice of clockwise and counter-clockwise. These two situations share the common feature that they are described in terms of top-dimensional behavior nearpbut not atp.For the general case, letMbe a topologicaln-manifold. Alocal orientationofMaround a pointpis a choice of generator of the group

H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right).

To see the geometric significance of this group, choose a chart aroundp.In that chart there is a neighborhood ofpwhich is an open ballBaround the originO.By theexcision theorem, $H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)$ is isomorphic to $H_{n}\left(B,B\setminus \{O\};\mathbf {Z} \right)$ .The ballBis contractible, so its homology groups vanish except in degree zero, and the space $B\O$ is an $(n - 1)$ -sphere, so its homology groups vanish except in degrees $n - 1$ and $0$ .A computation with thelong exact sequenceinrelative homologyshows that the above homology group is isomorphic to $H_{n-1}\left(S^{n-1};\mathbf {Z} \right)\cong \mathbf {Z}$ .A choice of generator therefore corresponds to a decision of whether, in the given chart, a sphere aroundpis positive or negative. A reflection of $R n$ through the origin acts by negation on $H_{n-1}\left(S^{n-1};\mathbf {Z} \right)$ ,so the geometric significance of the choice of generator is that it distinguishes charts from their reflections.

On a topological manifold, a transition function isorientation preservingif, at each pointpin its domain, it fixes the generators of $H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)$ .From here, the relevant definitions are the same as in the differentiable case. Anoriented atlasis one for which all transition functions are orientation preserving,Misorientableif it admits an oriented atlas, and when $n > 0$ ,anorientationofMis a maximal oriented atlas.

Intuitively, an orientation ofMought to define a unique local orientation ofMat each point. This is made precise by noting that any chart in the oriented atlas aroundpcan be used to determine a sphere aroundp,and this sphere determines a generator of $H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)$ .Moreover, any other chart aroundpis related to the first chart by an orientation preserving transition function, and this implies that the two charts yield the same generator, whence the generator is unique.

Purely homological definitions are also possible. Assuming thatMis closed and connected,Misorientableif and only if thenth homology group $H_{n}(M;\mathbf {Z} )$ is isomorphic to the integersZ.AnorientationofMis a choice of generator $α$ of this group. This generator determines an oriented atlas by fi xing a generator of the infinite cyclic group $H_{n}(M;\mathbf {Z} )$ and taking the oriented charts to be those for which $α$ pushes forward to the fixed generator. Conversely, an oriented atlas determines such a generator as compatible local orientations can be glued together to give a generator for the homology group $H_{n}(M;\mathbf {Z} )$ .^[4]

Orientation and cohomology

A manifoldMis orientable if and only if the firstStiefel–Whitney class $w_{1}(M)\in H^{1}(M;\mathbf {Z} /2)$ vanishes. In particular, if the first cohomology group withZ/2 coefficients is zero, then the manifold is orientable. Moreover, ifMis orientable andw₁vanishes, then $H^{0}(M;\mathbf {Z} /2)$ parametrizes the choices of orientations.^[5]This characterization of orientability extends toorientability of general vector bundlesoverM,not just the tangent bundle.

The orientation double cover

Around each point ofMthere are two local orientations. Intuitively, there is a way to move from a local orientation at a point $p$ to a local orientation at a nearby point $p'$ :when the two points lie in the same coordinate chart $U \to R n$ ,that coordinate chart defines compatible local orientations at $p$ and $p'$ .The set of local orientations can therefore be given a topology, and this topology makes it into a manifold.

More precisely, letObe the set of all local orientations ofM.To topologizeOwe will specify a subbase for its topology. LetUbe an open subset ofMchosen such that $H_{n}(M,M\setminus U;\mathbf {Z} )$ is isomorphic toZ.Assume that α is a generator of this group. For eachpinU,there is a pushforward function $H_{n}(M,M\setminus U;\mathbf {Z} )\to H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)$ .The codomain of this group has two generators, and α maps to one of them. The topology onOis defined so that

\{{\text{Image of }}\ Alpha {\text{ in }}H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)\colon p\in U\}

is open.

There is a canonical map $π: O \to M$ that sends a local orientation atptop.It is clear that every point ofMhas precisely two preimages under $π$ .In fact, $π$ is even a local homeomorphism, because the preimages of the open setsUmentioned above are homeomorphic to the disjoint union of two copies ofU.IfMis orientable, thenMitself is one of these open sets, soOis the disjoint union of two copies ofM.IfMis non-orientable, however, thenOis connected and orientable. The manifoldOis called theorientation double cover.

Manifolds with boundary

IfMis a manifold with boundary, then an orientation ofMis defined to be an orientation of its interior. Such an orientation induces an orientation of ∂M.Indeed, suppose that an orientation ofMis fixed. Let $U \to R n +$ be a chart at a boundary point ofMwhich, when restricted to the interior ofM,is in the chosen oriented atlas. The restriction of this chart to ∂Mis a chart of ∂M.Such charts form an oriented atlas for ∂M.

WhenMis smooth, at each pointpof ∂M,the restriction of the tangent bundle ofMto ∂Mis isomorphic to $T p \partial M \oplus R$ ,where the factor ofRis described by the inward pointing normal vector. The orientation ofT_p∂Mis defined by the condition that a basis ofT_p∂Mis positively oriented if and only if it, when combined with the inward pointing normal vector, defines a positively oriented basis ofT_pM.

Orientable double cover

Animation of the orientable double cover of theMöbius strip.

A closely related notion uses the idea ofcovering space.For a connected manifoldMtakeM^∗,the set of pairs (x,o) wherexis a point ofMandois an orientation atx;here we assumeMis either smooth so we can choose an orientation on the tangent space at a point or we usesingular homologyto define orientation. Then for every open, oriented subset ofMwe consider the corresponding set of pairs and define that to be an open set ofM^∗.This givesM^∗a topology and the projection sending (x,o) toxis then a 2-to-1 covering map. This covering space is called theorientable double cover,as it is orientable.M^∗is connected if and only ifMis not orientable.

Another way to construct this cover is to divide the loops based at a basepoint into either orientation-preserving or orientation-reversing loops. The orientation preserving loops generate a subgroup of the fundamental group which is either the whole group or ofindextwo. In the latter case (which means there is an orientation-reversing path), the subgroup corresponds to a connected double covering; this cover is orientable by construction. In the former case, one can simply take two copies ofM,each of which corresponds to a different orientation.

Orientation of vector bundles

A realvector bundle,whicha priorihas aGL(n)structure group,is calledorientablewhen thestructure groupmay bereducedto $GL^{+}(n)$ ,the group ofmatriceswith positivedeterminant.For thetangent bundle,this reduction is always possible if the underlying base manifold is orientable and in fact this provides a convenient way to define the orientability of asmoothrealmanifold:a smooth manifold is defined to be orientable if itstangent bundleis orientable (as a vector bundle). Note that as a manifold in its own right, the tangent bundle isalwaysorientable, even over nonorientable manifolds.

Related concepts

Lorentzian geometry

InLorentzian geometry,there are two kinds of orientability:space orientabilityandtime orientability.These play a role in thecausal structureof spacetime.^[6]In the context ofgeneral relativity,aspacetimemanifold is space orientable if, whenever two right-handed observers head off in rocket ships starting at the same spacetime point, and then meet again at another point, they remain right-handed with respect to one another. If a spacetime is time-orientable then the two observers will always agree on the direction of time at both points of their meeting. In fact, a spacetime is time-orientable if and only if any two observers can agree which of the two meetings preceded the other.^[7]

Formally, thepseudo-orthogonal groupO(p,q) has a pair ofcharacters:the space orientation character σ₊and the time orientation character σ₋,

\sigma _{\pm }:\operatorname {O} (p,q)\to \{-1,+1\}.

Their product σ = σ₊σ₋is the determinant, which gives the orientation character. A space-orientation of a pseudo-Riemannian manifold is identified with asectionof theassociated bundle

\operatorname {O} (M)\times _{\sigma _{+}}\{-1,+1\}

where O(M) is the bundle of pseudo-orthogonal frames. Similarly, a time orientation is a section of the associated bundle

\operatorname {O} (M)\times _{\sigma _{-}}\{-1,+1\}.

References

^Munroe, Marshall Evans (1963).Modern multidimensional calculus.Addison-Wesley. p. 263.
^Spivak, Michael(1965).Calculus on Manifolds.HarperCollins.ISBN 978-0-8053-9021-6.
^Hatcher, Allen(2001).Algebraic Topology.Cambridge University Press.ISBN 978-0521795401.
^Hatcher 2001,p. 236 Theorem 3.26(a)
^Lawson, H. Blaine;Michelsohn, Marie-Louise(1989).Spin Geometry.Princeton University Press.p. 79 Theorem 1.2.ISBN 0-691-08542-0.
^Hawking, S.W.;Ellis, G.F.R.(1973).The Large Scale Structure of Space-Time.Cambridge University Press.ISBN 0-521-20016-4.
^Hadley, Mark J. (2002)."The Orientability of Spacetime"(PDF).Classical and Quantum Gravity.19(17): 4565–71.arXiv:gr-qc/0202031v4.CiteSeerX10.1.1.340.8125.doi:10.1088/0264-9381/19/17/308.

External links

Orientation of manifoldsat the Manifold Atlas.
Orientation coveringat the Manifold Atlas.
Orientation of manifolds in generalized cohomology theoriesat the Manifold Atlas.
The Encyclopedia of Mathematics article onOrientation.

[1] Munroe, Marshall Evans (1963).Modern multidimensional calculus.Addison-Wesley. p. 263.

[2] Spivak, Michael(1965).Calculus on Manifolds.HarperCollins.ISBN 978-0-8053-9021-6.

[3] Hatcher, Allen(2001).Algebraic Topology.Cambridge University Press.ISBN 978-0521795401.

[4] Hatcher 2001,p. 236 Theorem 3.26(a)

[5] Lawson, H. Blaine;Michelsohn, Marie-Louise(1989).Spin Geometry.Princeton University Press.p. 79 Theorem 1.2.ISBN 0-691-08542-0.

[6] Hawking, S.W.;Ellis, G.F.R.(1973).The Large Scale Structure of Space-Time.Cambridge University Press.ISBN 0-521-20016-4.

[7] Hadley, Mark J. (2002)."The Orientability of Spacetime"(PDF).Classical and Quantum Gravity.19(17): 4565–71.arXiv:gr-qc/0202031v4.CiteSeerX10.1.1.340.8125.doi:10.1088/0264-9381/19/17/308.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

v t e Topology
Fields	General (point-set) Algebraic Combinatorial Continuum Differential Geometric low-dimensional Homology cohomology Set-theoretic Digital
Key concepts	Open set/Closed set Interior Continuity Space compact connected Hausdorff metric uniform Homotopy homotopy group fundamental group Simplicial complex CW complex Polyhedral complex Manifold Bundle (mathematics) Second-countable space Cobordism
Metrics and properties	Euler characteristic Betti number Winding number Chern number Orientability
Key results	Banach fixed-point theorem De Rham cohomology Invariance of domain Poincaré conjecture Tychonoff's theorem Urysohn's lemma
Category Mathematics portal Wikibook Wikiversity Topics general algebraic geometric Publications