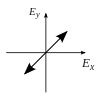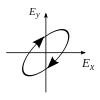Polarization (waves)

Circular polarization on rubber thread, converted to linear polarization

Polarization(alsopolarisation) is a property oftransverse waveswhich specifies the geometrical orientation of theoscillations.^[1]^[2]^[3]^[4]^[5]In a transverse wave, the direction of the oscillation is perpendicular to the direction of motion of the wave.^[4]A simple example of a polarized transverse wave is vibrations traveling along a taut string(see image),for example, in a musical instrument like aguitar string.Depending on how the string is plucked, the vibrations can be in a vertical direction, horizontal direction, or at any angle perpendicular to the string. In contrast, inlongitudinal waves,such assound wavesin a liquid or gas, the displacement of the particles in the oscillation is always in the direction of propagation, so these waves do not exhibit polarization. Transverse waves that exhibit polarization includeelectromagnetic wavessuch aslightandradio waves,gravitational waves,^[6]and transverse sound waves (shear waves) in solids.

Anelectromagnetic wavesuch as light consists of a coupled oscillatingelectric fieldandmagnetic fieldwhich are always perpendicular to each other; by convention, the "polarization" of electromagnetic waves refers to the direction of the electric field. Inlinear polarization,the fields oscillate in a single direction. Incircularorelliptical polarization,the fields rotate at a constant rate in a plane as the wave travels, either in theright-handor in the left-hand direction.

Light or other electromagnetic radiation from many sources, such as the sun, flames, andincandescent lamps,consists of short wave trains with an equal mixture of polarizations; this is calledunpolarized light.Polarized light can be produced by passing unpolarized light through apolarizer,which allows waves of only one polarization to pass through. The most common optical materials do not affect the polarization of light, but some materials—those that exhibitbirefringence,dichroism,oroptical activity—affect light differently depending on its polarization. Some of these are used to make polarizing filters. Light also becomes partially polarized when it reflects at an angle from a surface.

According toquantum mechanics,electromagnetic waves can also be viewed asstreams of particlescalledphotons.When viewed in this way, the polarization of an electromagnetic wave is determined by a quantum mechanical property of photons called theirspin.^[7]^[8]A photon has one of two possible spins: it can either spin in aright handsense or a left hand sense about its direction of travel. Circularly polarized electromagnetic waves are composed of photons with only one type of spin, either right- or left-hand. Linearly polarized waves consist of photons that are in a superposition of right and left circularly polarized states, with equal amplitude and phases synchronized to give oscillation in a plane.^[8]

Polarization is an important parameter in areas of science dealing with transverse waves, such asoptics,seismology,radio,andmicrowaves.Especially impacted are technologies such aslasers,wireless and optical fibertelecommunications,andradar.

Introduction

Wave propagation and polarization

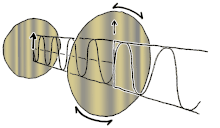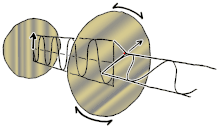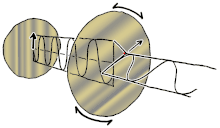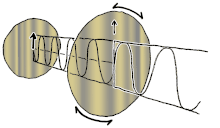
Most sources of light are classified as incoherent and unpolarized (or only "partially polarized" ) because they consist of a random mixture of waves having different spatial characteristics, frequencies (wavelengths), phases, and polarization states. However, for understanding electromagnetic waves and polarization in particular, it is easier to just consider coherentplane waves;these are sinusoidal waves of one particular direction (orwavevector), frequency, phase, and polarization state. Characterizing an optical system in relation to a plane wave with those given parameters can then be used to predict its response to a more general case, since a wave with any specified spatial structure can be decomposed into a combination of plane waves (its so-calledangular spectrum). Incoherent states can be modeledstochasticallyas a weighted combination of such uncorrelated waves with somedistributionof frequencies (itsspectrum), phases, and polarizations.

Transverse electromagnetic waves

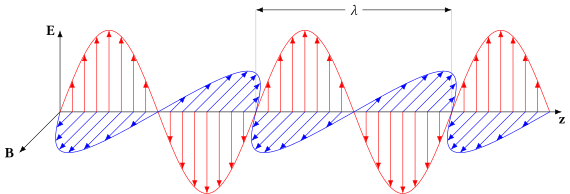
Electromagnetic waves(such as light), traveling in free space or anotherhomogeneous isotropic non-attenuatingmedium, are properly described astransverse waves,meaning that a plane wave's electric field vector $E$ and magnetic field $H$ are each in some direction perpendicular to (or "transverse" to) the direction of wave propagation; $E$ and $H$ are also perpendicular to each other. By convention, the "polarization" direction of an electromagnetic wave is given by its electric field vector. Considering a monochromaticplane waveof optical frequency $f$ (light of vacuum wavelength $λ$ has a frequency of $f = c/λ$ where $c$ is the speed of light), let us take the direction of propagation as the $z$ axis. Being a transverse wave the $E$ and $H$ fields must then contain components only in the $x$ and $y$ directions whereas $E z = H z = 0$ .Usingcomplex(orphasor) notation, the instantaneous physical electric and magnetic fields are given by thereal partsof the complex quantities occurring in the following equations. As a function of time $t$ and spatial position $z$ (since for a plane wave in the $+ z$ direction the fields have no dependence on $x$ or $y$ ) these complex fields can be written as: ${\vec {E}}(z,t)={\begin{bmatrix}e_{x}\\e_{y}\\0\end{bmatrix}}\;e^{i2\pi \left({\frac {z}{\lambda }}-{\frac {t}{T}}\right)}={\begin{bmatrix}e_{x}\\e_{y}\\0\end{bmatrix}}\;e^{i(kz-\ Omega t)}$ and ${\vec {H}}(z,t)={\begin{bmatrix}h_{x}\\h_{y}\\0\end{bmatrix}}\;e^{i2\pi \left({\frac {z}{\lambda }}-{\frac {t}{T}}\right)}={\begin{bmatrix}h_{x}\\h_{y}\\0\end{bmatrix}}\;e^{i(kz-\ Omega t)},$ where $λ = λ 0 / n$ is the wavelengthin the medium(whoserefractive indexis $n$ ) and $T = 1/ f$ is the period of the wave. Here $e x$ , $e y$ , $h x$ ,and $h y$ are complex numbers. In the second more compact form, as these equations are customarily expressed, these factors are described using thewavenumber $k = 2π n / λ 0$ andangular frequency(or "radian frequency" ) $ω = 2π f$ .In a more general formulation with propagationnotrestricted to the $+z$ direction, then the spatial dependence $kz$ is replaced by $k \to ∙ r \to$ where $k \to$ is called thewave vector,the magnitude of which is the wavenumber.

Thus the leading vectors $e$ and $h$ each contain up to two nonzero (complex) components describing the amplitude and phase of the wave's $x$ and $y$ polarization components (again, there can be no $z$ polarization component for a transverse wave in the $+ z$ direction). For a given medium with acharacteristic impedance $η$ , $h$ is related to $e$ by: ${\begin{aligned}h_{y}&={\frac {e_{x}}{\eta }}\\h_{x}&=-{\frac {e_{y}}{\eta }}.\end{aligned}}$

In a dielectric, $η$ is real and has the value $η 0 / n$ ,where $n$ is the refractive index and $η 0$ is theimpedance of free space.The impedance will be complex in a conducting medium. Note that given that relationship, thedot productof $E$ and $H$ must be zero: ${\begin{aligned}{\vec {E}}\left({\vec {r}},t\right)\cdot {\vec {H}}\left({\vec {r}},t\right)&=e_{x}h_{x}+e_{y}h_{y}+e_{z}h_{z}\\&=e_{x}\left(-{\frac {e_{y}}{\eta }}\right)+e_{y}\left({\frac {e_{x}}{\eta }}\right)+0\cdot 0\\&=0,\end{aligned}}$ indicating that these vectors areorthogonal(at right angles to each other), as expected.

Knowing the propagation direction ( $+ z$ in this case) and $η$ ,one can just as well specify the wave in terms of just $e x$ and $e y$ describing the electric field. The vector containing $e x$ and $e y$ (but without the $z$ component which is necessarily zero for a transverse wave) is known as aJones vector.In addition to specifying the polarization state of the wave, a general Jones vector also specifies the overall magnitude and phase of that wave. Specifically, theintensityof the light wave is proportional to the sum of the squared magnitudes of the two electric field components: $I=\left(\left|e_{x}\right|^{2}+\left|e_{y}\right|^{2}\right)\,{\frac {1}{2\eta }}$

However, the wave'sstate of polarizationis only dependent on the (complex) ratio of $e y$ to $e x$ .So let us just consider waves whose $| e x | 2 + | e y | 2 = 1$ ;this happens to correspond to an intensity of about0.00133W/m²in free space (where $η = η 0$ ). And because the absolute phase of a wave is unimportant in discussing its polarization state, let us stipulate that the phase of $e x$ is zero; in other words $e x$ is a real number while $e y$ may be complex. Under these restrictions, $e x$ and $e y$ can be represented as follows: ${\begin{aligned}e_{x}&={\sqrt {\frac {1+Q}{2}}}\\e_{y}&={\sqrt {\frac {1-Q}{2}}}\,e^{i\phi },\end{aligned}}$ where the polarization state is now fully parameterized by the value of $Q$ (such that $-1 < Q < 1$ ) and the relative phase $ϕ$ .

Non-transverse waves

In addition to transverse waves, there are many wave motions where the oscillation is not limited to directions perpendicular to the direction of propagation. These cases are far beyond the scope of the current article which concentrates on transverse waves (such as most electromagnetic waves in bulk media), but one should be aware of cases where the polarization of a coherent wave cannot be described simply using a Jones vector, as we have just done.

Just considering electromagnetic waves, we note that the preceding discussion strictly applies to plane waves in a homogeneous isotropic non-attenuating medium, whereas in ananisotropicmedium (such as birefringent crystals as discussed below) the electric or magnetic field may have longitudinal as well as transverse components. In those cases theelectric displacement $D$ andmagnetic flux density $B$ ^{[clarification needed]}still obey the above geometry but due to anisotropy in theelectric susceptibility(or in themagnetic permeability), now given by atensor,the direction of $E$ (or $H$ ) may differ from that of $D$ (or $B$ ). Even in isotropic media, so-calledinhomogeneous wavescan be launched into a medium whose refractive index has a significant imaginary part (or "extinction coefficient") such as metals;^{[clarification needed]}these fields are also not strictly transverse.^[9]^{: 179–184}^[10]^: 51–52Surface wavesor waves propagating in awaveguide(such as anoptical fiber) are generallynottransverse waves, but might be described as an electric or magnetictransverse mode,or a hybrid mode.

Even in free space, longitudinal field components can be generated in focal regions, where the plane wave approximation breaks down. An extreme example isradiallyor tangentially polarized light, at the focus of which the electric or magnetic field respectively isentirelylongitudinal (along the direction of propagation).^[11]

Forlongitudinal wavessuch assound wavesinfluids,the direction of oscillation is by definition along the direction of travel, so the issue of polarization is normally not even mentioned. On the other hand, sound waves in a bulksolidcan be transverse as well as longitudinal, for a total of three polarization components. In this case, the transverse polarization is associated with the direction of theshear stressand displacement in directions perpendicular to the propagation direction, while the longitudinal polarization describes compression of the solid and vibration along the direction of propagation. The differential propagation of transverse and longitudinal polarizations is important inseismology.

Polarization state

Electric field oscillation

Polarization can be defined in terms of pure polarization states with only a coherent sinusoidal wave at one optical frequency. The vector in the adjacent diagram might describe the oscillation of the electric field emitted by a single-mode laser (whose oscillation frequency would be typically10¹⁵times faster). The field oscillates in the $xy$ -plane, along the page, with the wave propagating in the $z$ direction, perpendicular to the page. The first two diagrams below trace the electric field vector over a complete cycle for linear polarization at two different orientations; these are each considered a distinctstate of polarization(SOP). The linear polarization at 45° can also be viewed as the addition of a horizontally linearly polarized wave (as in the leftmost figure) and a vertically polarized wave of the same amplitudein the same phase.

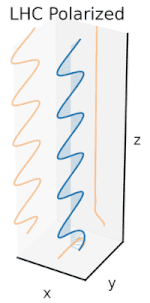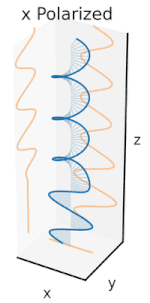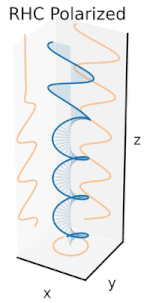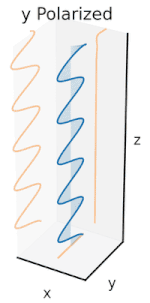
Now if one were to introduce aphase shiftin between those horizontal and vertical polarization components, one would generally obtain elliptical polarization^[12]as is shown in the third figure. When the phase shift is exactly ±90°, and the amplitudes are the same, thencircular polarizationis produced (fourth and fifth figures). Circular polarization can be created by sending linearly polarized light through aquarter-wave plateoriented at 45° to the linear polarization to create two components of the same amplitude with the required phase shift. The superposition of the original and phase-shifted components causes a rotating electric field vector, which is depicted in the animation on the right. Note that circular or elliptical polarization can involve either a clockwise or counterclockwise rotation of the field, depending on the relative phases of the components. These correspond to distinct polarization states, such as the two circular polarizations shown above.

The orientation of the $x$ and $y$ axes used in this description is arbitrary. The choice of such a coordinate system and viewing the polarization ellipse in terms of the $x$ and $y$ polarization components, corresponds to the definition of the Jones vector (below) in terms of thosebasispolarizations. Axes are selected to suit a particular problem, such as $x$ being in the plane of incidence. Since there are separate reflection coefficients for the linear polarizations in and orthogonal to the plane of incidence (pandspolarizations, see below), that choice greatly simplifies the calculation of a wave's reflection from a surface.

Any pair oforthogonalpolarization states may be used as basis functions, not just linear polarizations. For instance, choosing right and left circular polarizations as basis functions simplifies the solution of problems involving circular birefringence (optical activity) or circular dichroism.

Polarization ellipse

For a purely polarized monochromatic wave the electric field vector over one cycle of oscillation traces out an ellipse. A polarization state can then be described in relation to the geometrical parameters of the ellipse, and its "handedness", that is, whether the rotation around the ellipse is clockwise or counter clockwise. One parameterization of the elliptical figure specifies theorientation angle $ψ$ ,defined as the angle between the major axis of the ellipse and the $x$ -axis^[13]along with theellipticity $ε = a/b$ ,the ratio of the ellipse's major to minor axis.^[14]^[15]^[16](also known as theaxial ratio). The ellipticity parameter is an alternative parameterization of an ellipse'seccentricity ${\textstyle e={\sqrt {1-b^{2}/a^{2}}},}$ or theellipticity angle, ${\textstyle \chi =\arctan b/a}$ ${\textstyle =\arctan 1/\varepsilon }$ as is shown in the figure.^[13]The angle $χ$ is also significant in that the latitude (angle from the equator) of the polarization state as represented on the Poincaré sphere (see below) is equal to $\pm2 χ$ .The special cases of linear and circular polarization correspond to an ellipticity $ε$ of infinity and unity (or $χ$ of zero and 45°) respectively.

Jones vector

Full information on a completely polarized state is also provided by the amplitude and phase of oscillations in two components of the electric field vector in the plane of polarization. This representation was used above to show how different states of polarization are possible. The amplitude and phase information can be conveniently represented as a two-dimensionalcomplexvector (theJones vector):

$\mathbf {e} ={\begin{bmatrix}a_{1}e^{i\theta _{1}}\\a_{2}e^{i\theta _{2}}\end{bmatrix}}.$

Here $a 1$ and $a 2$ denote the amplitude of the wave in the two components of the electric field vector, while $θ 1$ and $θ 2$ represent the phases. The product of a Jones vector with a complex number of unitmodulusgives a different Jones vector representing the same ellipse, and thus the same state of polarization. The physical electric field, as the real part of the Jones vector, would be altered but the polarization state itself is independent ofabsolute phase.Thebasisvectors used to represent the Jones vector need not represent linear polarization states (i.e. bereal). In general any two orthogonal states can be used, where an orthogonal vector pair is formally defined as one having a zeroinner product.A common choice is left and right circular polarizations, for example to model the different propagation of waves in two such components in circularly birefringent media (see below) or signal paths of coherent detectors sensitive to circular polarization.

Coordinate frame

Regardless of whether polarization state is represented using geometric parameters or Jones vectors, implicit in the parameterization is the orientation of the coordinate frame. This permits a degree of freedom, namely rotation about the propagation direction. When considering light that is propagating parallel to the surface of the Earth, the terms "horizontal" and "vertical" polarization are often used, with the former being associated with the first component of the Jones vector, or zero azimuth angle. On the other hand, inastronomytheequatorial coordinate systemis generally used instead, with the zero azimuth (or position angle, as it is more commonly called in astronomy to avoid confusion with thehorizontal coordinate system) corresponding to due north.

sandpdesignations

Electromagnetic vectors for

E

,

B

,and

k

with

E = E (x, y)

along with 3 planar projections and a deformation surface of total electric field. The light is alwayss-polarized in the

xy

-plane.

θ

is the polar angle of

k

and

φ E

is the azimuthal angle of

E

.

Another coordinate system frequently used relates to theplane of incidence.This is the plane made by the incoming propagation direction and the vector perpendicular to the plane of an interface, in other words, the plane in which the ray travels before and after reflection or refraction. The component of the electric field parallel to this plane is termedp-like(parallel) and the component perpendicular to this plane is termeds-like(fromsenkrecht,German for 'perpendicular'). Polarized light with its electric field along the plane of incidence is thus denotedp-polarized,while light whose electric field is normal to the plane of incidence is calleds-polarized.P-polarization is commonly referred to astransverse-magnetic(TM), and has also been termedpi-polarizedor $π$ -polarized,ortangential plane polarized.S-polarization is also calledtransverse-electric(TE), as well assigma-polarizedorσ-polarized,orsagittal plane polarized.

Degree of polarization

Degree of polarization(DOP) is a quantity used to describe the portion of anelectromagnetic wavewhich is polarized.DOPcan be calculated from theStokes parameters.A perfectly polarized wave has aDOPof 100%, whereas an unpolarized wave has aDOPof 0%. A wave which is partially polarized, and therefore can be represented by a superposition of a polarized and unpolarized component, will have aDOPsomewhere in between 0 and 100%.DOPis calculated as the fraction of the total power that is carried by the polarized component of the wave.

DOPcan be used to map thestrainfield in materials when considering theDOPof thephotoluminescence.The polarization of the photoluminescence is related to the strain in a material by way of the given material'sphotoelasticity tensor.

DOPis also visualized using thePoincaré sphererepresentation of a polarized beam. In this representation,DOPis equal to the length of thevectormeasured from the center of the sphere.

Unpolarized and partially polarized light

Unpolarized lightislightwith a random, time-varyingpolarization. Natural light, like most other common sources of visible light, is produced independently by a large number of atoms or molecules whose emissions areuncorrelated.

Unpolarized light can be produced from theincoherentcombination of vertical and horizontallinearly polarizedlight, or right- and left-handedcircularly polarizedlight.^[17] Conversely, the two constituent linearly polarized states of unpolarized light cannot form aninterference pattern,even if rotated into alignment (Fresnel–Arago 3rd law).^[18]

A so-calleddepolarizeracts on a polarized beam to create one in which the polarization varies so rapidly across the beam that it may be ignored in the intended applications. Conversely, apolarizeracts on an unpolarized beam or arbitrarily polarized beam to create one which is polarized.

Unpolarized light can be described as a mixture of two independent oppositely polarized streams, each with half the intensity.^[19]^[20]Light is said to bepartially polarizedwhen there is more power in one of these streams than the other. At any particular wavelength, partially polarized light can be statistically described as the superposition of a completely unpolarized component and a completely polarized one.^[21]^{: 346–347}^[22]^: 330One may then describe the light in terms of thedegree of polarizationand the parameters of the polarized component. That polarized component can be described in terms of a Jones vector or polarization ellipse. However, in order to also describe the degree of polarization, one normally employs Stokes parameters to specify a state of partial polarization.^[21]^{: 351, 374–375}

Implications for reflection and propagation

Polarization in wave propagation

In avacuum,the components of the electric field propagate at thespeed of light,so that the phase of the wave varies in space and time while the polarization state does not. That is, the electric field vector $e$ of a plane wave in the $+ z$ direction follows: $\mathbf {e} (z+\Delta z,t+\Delta t)=\mathbf {e} (z,t)e^{ik(c\Delta t-\Delta z)},$

where $k$ is thewavenumber.As noted above, the instantaneous electric field is the real part of the product of the Jones vector times the phase factor $e^{-i\ Omega t}$ .When an electromagnetic wave interacts with matter, its propagation is altered according to the material's (complex)index of refraction.When the real or imaginary part of that refractive index is dependent on the polarization state of a wave, properties known asbirefringenceand polarizationdichroism(ordiattenuation) respectively, then the polarization state of a wave will generally be altered.

In such media, an electromagnetic wave with any given state of polarization may be decomposed into two orthogonally polarized components that encounter differentpropagation constants.The effect of propagation over a given path on those two components is most easily characterized in the form of a complex2 × 2transformationmatrix $J$ known as aJones matrix: $\mathbf {e'} =\mathbf {J} \mathbf {e}.$

The Jones matrix due to passage through a transparent material is dependent on the propagation distance as well as the birefringence. The birefringence (as well as the average refractive index) will generally bedispersive,that is, it will vary as a function of optical frequency (wavelength). In the case of non-birefringent materials, however, the2 × 2Jones matrix is the identity matrix (multiplied by a scalarphase factorand attenuation factor), implying no change in polarization during propagation.

For propagation effects in two orthogonal modes, the Jones matrix can be written as $\mathbf {J} =\mathbf {T} {\begin{bmatrix}g_{1}&0\\0&g_{2}\end{bmatrix}}\mathbf {T} ^{-1},$

where $g 1$ and $g 2$ are complex numbers describing thephase delayand possibly the amplitude attenuation due to propagation in each of the two polarizationeigenmodes. $T$ is aunitary matrixrepresenting a change of basis from these propagation modes to the linear system used for the Jones vectors; in the case of linear birefringence or diattenuation the modes are themselves linear polarization states so $T$ and $T -1$ can be omitted if the coordinate axes have been chosen appropriately.

Birefringence

In abirefringentsubstance, electromagnetic waves of different polarizations travel at different speeds (phase velocities). As a result, when unpolarized waves travel through a plate of birefringent material, one polarization component has a shorter wavelength than the other, resulting in aphase differencebetween the components which increases the further the waves travel through the material. The Jones matrix is aunitary matrix: $| g 1 | = | g 2 | = 1$ .Media termed diattenuating (ordichroicin the sense of polarization), in which only the amplitudes of the two polarizations are affected differentially, may be described using aHermitian matrix(generally multiplied by a common phase factor). In fact, sinceanymatrix may be written as the product of unitary and positive Hermitian matrices, light propagation through any sequence of polarization-dependent optical components can be written as the product of these two basic types of transformations.

In birefringent media there is no attenuation, but two modes accrue a differential phase delay. Well known manifestations of linear birefringence (that is, in which the basis polarizations are orthogonal linear polarizations) appear in opticalwave plates/retarders and many crystals. If linearly polarized light passes through a birefringent material, its state of polarization will generally change,unlessits polarization direction is identical to one of those basis polarizations. Since the phase shift, and thus the change in polarization state, is usually wavelength-dependent, such objects viewed under white light in between two polarizers may give rise to colorful effects, as seen in the accompanying photograph.

Circular birefringence is also termedoptical activity,especially inchiralfluids, orFaraday rotation,when due to the presence of a magnetic field along the direction of propagation. When linearly polarized light is passed through such an object, it will exit still linearly polarized, but with the axis of polarization rotated. A combination of linear and circular birefringence will have as basis polarizations two orthogonal elliptical polarizations; however, the term "elliptical birefringence" is rarely used.

Paths taken by vectors in the Poincaré sphere under birefringence. The propagation modes (rotation axes) are shown with red, blue, and yellow lines, the initial vectors by thick black lines, and the paths they take by colored ellipses (which represent circles in three dimensions).

One can visualize the case of linear birefringence (with two orthogonal linear propagation modes) with an incoming wave linearly polarized at a 45° angle to those modes. As a differential phase starts to accrue, the polarization becomes elliptical, eventually changing to purely circular polarization (90° phase difference), then to elliptical and eventually linear polarization (180° phase) perpendicular to the original polarization, then through circular again (270° phase), then elliptical with the original azimuth angle, and finally back to the original linearly polarized state (360° phase) where the cycle begins anew. In general the situation is more complicated and can be characterized as arotationin the Poincaré sphere about the axis defined by the propagation modes. Examples for linear (blue), circular (red), and elliptical (yellow)birefringenceare shown in the figure on the left. The total intensity and degree of polarization are unaffected. If the path length in the birefringent medium is sufficient, the two polarization components of a collimated beam (orray) can exit the material with a positional offset, even though their final propagation directions will be the same (assuming the entrance face and exit face are parallel). This is commonly viewed usingcalcite crystals,which present the viewer with two slightly offset images, in opposite polarizations, of an object behind the crystal. It was this effect that provided the first discovery of polarization, byErasmus Bartholinusin 1669.

Dichroism

Media in which transmission of one polarization mode is preferentially reduced are calleddichroicordiattenuating.Like birefringence, diattenuation can be with respect to linear polarization modes (in a crystal) or circular polarization modes (usually in a liquid).

Devices that block nearly all of the radiation in one mode are known aspolarizing filtersor simply "polarizers".This corresponds to $g 2 = 0$ in the above representation of the Jones matrix. The output of an ideal polarizer is a specific polarization state (usually linear polarization) with an amplitude equal to the input wave's original amplitude in that polarization mode. Power in the other polarization mode is eliminated. Thus if unpolarized light is passed through an ideal polarizer (where $g 1 = 1$ and $g 2 = 0$ ) exactly half of its initial power is retained. Practical polarizers, especially inexpensive sheet polarizers, have additional loss so that $g 1 < 1$ .However, in many instances the more relevant figure of merit is the polarizer'sdegree of polarizationorextinction ratio,which involve a comparison of $g 1$ to $g 2$ .Since Jones vectors refer to waves' amplitudes (rather thanintensity), when illuminated by unpolarized light the remaining power in the unwanted polarization will be $(g 2 / g 1) 2$ of the power in the intended polarization.

Specular reflection

In addition to birefringence and dichroism in extended media, polarization effects describable using Jones matrices can also occur at (reflective) interface between two materials of differentrefractive index.These effects are treated by theFresnel equations.Part of the wave is transmitted and part is reflected; for a given material those proportions (and also the phase of reflection) are dependent on theangle of incidenceand are different for thes- andp-polarizations. Therefore, the polarization state of reflected light (even if initially unpolarized) is generally changed.

A stack of plates at Brewster's angle to a beam reflects off a fraction of thes-polarized light at each surface, leaving (after many such plates) a mainlyp-polarized beam.

Any light striking a surface at a special angle of incidence known asBrewster's angle,where the reflection coefficient forp-polarization is zero, will be reflected with only thes-polarization remaining. This principle is employed in the so-called "pile of plates polarizer" (see figure) in which part of thes-polarization is removed by reflection at each Brewster angle surface, leaving only thep-polarization after transmission through many such surfaces. The generally smaller reflection coefficient of thep-polarization is also the basis ofpolarized sunglasses;by blocking thes- (horizontal) polarization, most of the glare due to reflection from a wet street, for instance, is removed.^[23]^{: 348–350}

In the important special case of reflection at normal incidence (not involving anisotropic materials) there is no particulars- orp-polarization. Both the $x$ and $y$ polarization components are reflected identically, and therefore the polarization of the reflected wave is identical to that of the incident wave. However, in the case of circular (or elliptical) polarization, the handedness of the polarization state is thereby reversed, since byconventionthis is specified relative to the direction of propagation. The circular rotation of the electric field around the $x-y$ axes called "right-handed" for a wave in the $+ z$ direction is "left-handed" for a wave in the $- z$ direction. But in the general case of reflection at a nonzero angle of incidence, no such generalization can be made. For instance, right-circularly polarized light reflected from a dielectric surface at a grazing angle, will still be right-handed (but elliptically) polarized. Linear polarized light reflected from a metal at non-normal incidence will generally become elliptically polarized. These cases are handled using Jones vectors acted upon by the different Fresnel coefficients for thes- andp-polarization components.

Measurement techniques involving polarization

Some optical measurement techniques are based on polarization. In many other optical techniques polarization is crucial or at least must be taken into account and controlled; such examples are too numerous to mention.

Measurement of stress

Inengineering,the phenomenon ofstress induced birefringenceallows for stresses in transparent materials to be readily observed. As noted above and seen in the accompanying photograph, the chromaticity of birefringence typically creates colored patterns when viewed in between two polarizers. As external forces are applied, internal stress induced in the material is thereby observed. Additionally, birefringence is frequently observed due to stresses "frozen in" at the time of manufacture. This is famously observed incellophanetape whose birefringence is due to the stretching of the material during the manufacturing process.

Ellipsometry

Ellipsometry is a powerful technique for the measurement of the optical properties of a uniform surface. It involves measuring the polarization state of light following specular reflection from such a surface. This is typically done as a function of incidence angle or wavelength (or both). Since ellipsometry relies on reflection, it is not required for the sample to be transparent to light or for its back side to be accessible.

Ellipsometry can be used to model the (complex) refractive index of a surface of a bulk material. It is also very useful in determining parameters of one or morethin filmlayers deposited on a substrate. Due to theirreflection properties,not only are the predicted magnitude of thepandspolarization components, but their relative phase shifts upon reflection, compared to measurements using an ellipsometer. A normal ellipsometer does not measure the actual reflection coefficient (which requires careful photometric calibration of the illuminating beam) but the ratio of thepandsreflections, as well as change of polarization ellipticity (hence the name) induced upon reflection by the surface being studied. In addition to use in science and research, ellipsometers are usedin situto control production processes for instance.^[24]^: 585ff^[25]^: 632

Geology

Photomicrograph of avolcanic sand grain;upper picture is plane-polarized light, bottom picture is cross-polarized light, scale box at left-center is 0.25 millimeter.

The property of (linear) birefringence is widespread in crystallineminerals,and indeed was pivotal in the initial discovery of polarization. Inmineralogy,this property is frequently exploited using polarizationmicroscopes,for the purpose of identifying minerals. Seeoptical mineralogyfor more details.^[26]^{: 163–164}

Sound waves in solid materials exhibit polarization. Differential propagation of the three polarizations through the earth is a crucial in the field ofseismology.Horizontally and vertically polarized seismic waves (shear waves) are termed SH and SV, while waves with longitudinal polarization (compressional waves) are termed P-waves.^[27]^: 48–50^[28]^: 56–57

Autopsy

Similarly, polarization microscopes can be used to aid in the detection of foreign matter in biological tissue slices if it is birefringent; autopsies often mention (a lack of or presence of) "polarizable foreign debris."^[29]

Chemistry

We have seen (above) that the birefringence of a type of crystal is useful in identifying it, and thus detection of linear birefringence is especially useful ingeologyandmineralogy.Linearly polarized light generally has its polarization state altered upon transmission through such a crystal, making it stand out when viewed in between two crossed polarizers, as seen in the photograph, above. Likewise, in chemistry, rotation of polarization axes in a liquid solution can be a useful measurement. In a liquid, linear birefringence is impossible, but there may be circular birefringence when a chiral molecule is in solution. When the right and left handedenantiomersof such a molecule are present in equal numbers (a so-calledracemicmixture) then their effects cancel out. However, when there is only one (or a preponderance of one), as is more often the case fororganic molecules,a net circular birefringence (oroptical activity) is observed, revealing the magnitude of that imbalance (or the concentration of the molecule itself, when it can be assumed that only one enantiomer is present). This is measured using apolarimeterin which polarized light is passed through a tube of the liquid, at the end of which is another polarizer which is rotated in order to null the transmission of light through it.^[23]^{: 360–365}^[30]

Astronomy

In many areas ofastronomy,the study of polarized electromagnetic radiation fromouter spaceis of great importance. Although not usually a factor in thethermal radiationofstars,polarization is also present in radiation from coherentastronomical sources(e.g. hydroxyl or methanolmasers), and incoherent sources such as the large radio lobes in active galaxies, and pulsar radio radiation (which may, it is speculated, sometimes be coherent), and is also imposed upon starlight by scattering frominterstellar dust.Apart from providing information on sources of radiation and scattering, polarization also probes the interstellar magnetic field viaFaraday rotation.^[31]^{: 119, 124}^[32]^{: 336–337}The polarization of thecosmic microwave backgroundis being used to study the physics of the very early universe.^[33]^[34]Synchrotron radiationis inherently polarized. It has been suggested that astronomical sources caused thechiralityof biological molecules on Earth,^[35]but chirality selection on inorganic crystals has been proposed as an alternative theory.^[36]

Applications and examples

Polarized sunglasses

Effect of a polarizer on reflection from mud flats. In the picture on the left, the horizontally oriented polarizer preferentially transmits those reflections; rotating the polarizer by 90° (right) as one would view using polarized sunglasses blocks almost allspecularly reflectedsunlight.

Unpolarized light, after being reflected by a specular (shiny) surface, generally obtains a degree of polarization. This phenomenon was observed in the early 1800s by the mathematicianÉtienne-Louis Malus,after whomMalus's lawis named. Polarizingsunglassesexploit this effect to reduce glare from reflections by horizontal surfaces, notably the road ahead viewed at a grazing angle.

Wearers of polarized sunglasses will occasionally observe inadvertent polarization effects such as color-dependent birefringent effects, for example intoughened glass(e.g., car windows) or items made from transparentplastics,in conjunction with natural polarization by reflection or scattering. The polarized light from LCD monitors (see below) is extremely conspicuous when these are worn.

Sky polarization and photography

The effects of apolarizing filter(right image) on the sky in a photograph

Polarization is observed in the light of thesky,as this is due to sunlightscatteredbyaerosolsas it passes throughEarth's atmosphere.Thescatteredlight produces the brightness and color in clear skies. This partial polarization of scattered light can be used to darken the sky in photographs, increasing the contrast. This effect is most strongly observed at points on the sky making a 90° angle to the Sun. Polarizing filters use these effects to optimize the results of photographing scenes in which reflection or scattering by the sky is involved.^[23]^{: 346–347}^[37]^{: 495–499}

Sky polarization has been used for orientation in navigation. ThePfund sky compasswas used in the 1950s when navigating near the poles of theEarth's magnetic fieldwhen neither thesunnorstarswere visible (e.g., under daytimecloudortwilight). It has been suggested, controversially, that theVikingsexploited a similar device (the "sunstone") in their extensive expeditions across theNorth Atlanticin the 9th–11th centuries, before the arrival of themagnetic compassfrom Asia to Europe in the 12th century. Related to the sky compass is the "polar clock",invented byCharles Wheatstonein the late 19th century.^[38]^: 67–69

Display technologies

The principle ofliquid-crystal display(LCD) technology relies on the rotation of the axis of linear polarization by the liquid crystal array. Light from thebacklight(or the back reflective layer, in devices not including or requiring a backlight) first passes through a linear polarizing sheet. That polarized light passes through the actual liquid crystal layer which may be organized in pixels (for a TV or computer monitor) or in another format such as aseven-segment displayor one with custom symbols for a particular product. The liquid crystal layer is produced with a consistent right (or left) handed chirality, essentially consisting of tinyhelices.This causes circular birefringence, and is engineered so that there is a 90 degree rotation of the linear polarization state. However, when a voltage is applied across a cell, the molecules straighten out, lessening or totally losing the circular birefringence. On the viewing side of the display is another linear polarizing sheet, usually oriented at 90 degrees from the one behind the active layer. Therefore, when the circular birefringence is removed by the application of a sufficient voltage, the polarization of the transmitted light remains at right angles to the front polarizer, and the pixel appears dark. With no voltage, however, the 90 degree rotation of the polarization causes it to exactly match the axis of the front polarizer, allowing the light through. Intermediate voltages create intermediate rotation of the polarization axis and the pixel has an intermediate intensity. Displays based on this principle are widespread, and now are used in the vast majority of televisions, computer monitors and video projectors, rendering the previousCRTtechnology essentially obsolete. The use of polarization in the operation of LCD displays is immediately apparent to someone wearing polarized sunglasses, often making the display unreadable.

In a totally different sense, polarization encoding has become the leading (but not sole) method for delivering separate images to the left and right eye instereoscopicdisplays used for3D movies.This involves separate images intended for each eye either projected from two different projectors with orthogonally oriented polarizing filters or, more typically, from a single projector with time multiplexed polarization (a fast alternating polarization device for successive frames).Polarized 3D glasseswith suitable polarizing filters ensure that each eye receives only the intended image. Historically such systems used linear polarization encoding because it was inexpensive and offered good separation. However, circular polarization makes separation of the two images insensitive to tilting of the head, and is widely used in 3-D movie exhibition today, such as the system fromRealD.Projecting such images requires screens that maintain the polarization of the projected light when viewed in reflection (such assilver screens); a normal diffuse white projection screen causes depolarization of the projected images, making it unsuitable for this application.

Although now obsolete, CRT computer displays suffered from reflection by the glass envelope, causing glare from room lights and consequently poor contrast. Several anti-reflection solutions were employed to ameliorate this problem. One solution utilized the principle of reflection of circularly polarized light. A circular polarizing filter in front of the screen allows for the transmission of (say) only right circularly polarized room light. Now, right circularly polarized light (depending on theconventionused) has its electric (and magnetic) field direction rotating clockwise while propagating in the +z direction. Upon reflection, the field still has the same direction of rotation, but now propagation is in the −z direction making the reflected waveleftcircularly polarized. With the right circular polarization filter placed in front of the reflecting glass, the unwanted light reflected from the glass will thus be in very polarization state that isblockedby that filter, eliminating the reflection problem. The reversal of circular polarization on reflection and elimination of reflections in this manner can be easily observed by looking in a mirror while wearing 3-D movie glasses which employ left- and right-handed circular polarization in the two lenses. Closing one eye, the other eye will see a reflection in which it cannot see itself; that lens appears black. However, the other lens (of the closed eye) will have the correct circular polarization allowing the closed eye to be easily seen by the open one.

Radio transmission and reception

Allradio(and microwave)antennasused for transmitting or receiving are intrinsically polarized. They transmit in (or receive signals from) a particular polarization, being totally insensitive to the opposite polarization; in certain cases that polarization is a function of direction. Most antennas are nominally linearly polarized, but elliptical and circular polarization is a possibility. In the case of linear polarization, the same kind of filtering as described above, is possible. In the case of elliptical polarization (circular polarization is in reality just a kind of elliptical polarization where the length of both elasticity factors is the same), filtering out a single angle (e.g. 90°) will have virtually no impact as the wave at any time can be in any of the 360 degrees.

The vast majority of antennas are linearly polarized. In fact it can be shown from considerations of symmetry that an antenna that lies entirely in a plane which also includes the observer, canonlyhave its polarization in the direction of that plane. This applies to many cases, allowing one to easily infer such an antenna's polarization at an intended direction of propagation. So a typical rooftopYagiorlog-periodic antennawith horizontal conductors, as viewed from a second station toward the horizon, is necessarily horizontally polarized. But a vertical "whip antenna"or AM broadcast tower used as an antenna element (again, for observers horizontally displaced from it) will transmit in the vertical polarization. Aturnstile antennawith its four arms in the horizontal plane, likewise transmits horizontally polarized radiation toward the horizon. However, when that same turnstile antenna is used in the "axial mode" (upwards, for the same horizontally-oriented structure) its radiation is circularly polarized. At intermediate elevations it is elliptically polarized.

Polarization is important in radio communications because, for instance, if one attempts to use a horizontally polarized antenna to receive a vertically polarized transmission, the signal strength will be substantially reduced (or under very controlled conditions, reduced to nothing). This principle is used insatellite televisionin order to double the channel capacity over a fixed frequency band. The same frequency channel can be used for two signals broadcast in opposite polarizations. By adjusting the receiving antenna for one or the other polarization, either signal can be selected without interference from the other.

Especially due to the presence of theground,there are some differences in propagation (and also in reflections responsible for TVghosting) between horizontal and vertical polarizations. AM and FM broadcast radio usually use vertical polarization, while television uses horizontal polarization. At low frequencies especially, horizontal polarization is avoided. That is because the phase of a horizontally polarized wave is reversed upon reflection by the ground. A distant station in the horizontal direction will receive both the direct and reflected wave, which thus tend to cancel each other. This problem is avoided with vertical polarization. Polarization is also important in the transmission ofradarpulses and reception of radar reflections by the same or a different antenna. For instance, back scattering of radar pulses by rain drops can be avoided by using circular polarization. Just as specular reflection of circularly polarized light reverses the handedness of the polarization, as discussed above, the same principle applies to scattering by objects much smaller than a wavelength such as rain drops. On the other hand, reflection of that wave by an irregular metal object (such as an airplane) will typically introduce a change in polarization and (partial) reception of the return wave by the same antenna.

The effect offree electronsin theionosphere,in conjunction with theearth's magnetic field,causesFaraday rotation,a sort of circular birefringence. This is the same mechanism which can rotate the axis of linear polarization by electrons ininterstellar spaceas mentionedbelow.The magnitude of Faraday rotation caused by such a plasma is greatly exaggerated at lower frequencies, so at the higher microwave frequencies used by satellites the effect is minimal. However, medium orshort wavetransmissions received followingrefraction by the ionosphereare strongly affected. Since a wave's path through the ionosphere and the earth's magnetic field vector along such a path are rather unpredictable, a wave transmitted with vertical (or horizontal) polarization will generally have a resulting polarization in an arbitrary orientation at the receiver.

Polarization and vision

Manyanimalsare capable of perceiving some of the components of the polarization of light, e.g., linear horizontally polarized light. This is generally used for navigational purposes, since the linear polarization of sky light is always perpendicular to the direction of the sun. This ability is very common among theinsects,includingbees,which use this information to orient theircommunicative dances.^[38]^{: 102–103}Polarization sensitivity has also been observed in species ofoctopus,squid,cuttlefish,andmantis shrimp.^[38]^{: 111–112}In the latter case, one species measures all six orthogonal components of polarization, and is believed to have optimal polarization vision.^[39]The rapidly changing, vividly colored skin patterns of cuttlefish, used for communication, also incorporate polarization patterns, and mantis shrimp are known to have polarization selective reflective tissue. Sky polarization was thought to be perceived bypigeons,which was assumed to be one of their aids inhoming,but research indicates this is a popular myth.^[40]

The nakedhuman eyeis weakly sensitive to polarization, without the need for intervening filters. Polarized light creates a very faint pattern near the center of the visual field, calledHaidinger's brush.This pattern is very difficult to see, but with practice one can learn to detect polarized light with the naked eye.^[38]^: 118

Angular momentum using circular polarization

It is well known that electromagnetic radiation carries a certain linearmomentumin the direction of propagation. In addition, however, light carries a certainangular momentumif it is circularly polarized (or partially so). In comparison with lower frequencies such as microwaves, the amount ofangular momentum in light,even of pure circular polarization, compared to the same wave's linear momentum (orradiation pressure) is very small and difficult to even measure. However, it was utilized in an experiment to achieve speeds of up to 600 million revolutions per minute.^[41]^[42]

References

Cited references

^Shipman, James; Wilson, Jerry D.; Higgins, Charles A. (2015).An Introduction to Physical Science, 14th Ed.Cengage Learning. p. 187.ISBN 978-1-305-54467-3.
^Muncaster, Roger (1993).A-level Physics.Nelson Thornes. pp. 465–467.ISBN 0-7487-1584-3.
^Singh, Devraj (2015).Fundamentals of Optics, 2nd Ed.PHI Learning Pvt. Ltd. p. 453.ISBN 978-8120351462.
^^a ^bAvadhanulu, M. N. (1992).A Textbook of Engineering Physics.S. Chand Publishing. pp. 198–199.ISBN 8121908175.
^Desmarais, Louis (1997).Applied Electro Optics.Pearson Education. pp. 162–163.ISBN 0-13-244182-9.
^Le Tiec, A.; Novak, J. (July 2016). "Theory of Gravitational Waves".An Overview of Gravitational Waves.pp. 1–41.arXiv:1607.04202.doi:10.1142/9789813141766_0001.ISBN 978-981-314-175-9.S2CID 119283594.
^Lipson, Stephen G.; Lipson, Henry; Tannhauser, David Stefan (1995).Optical Physics.Cambridge University Press. pp. 125–127.ISBN 978-0-521-43631-1.
^^a ^bWaldman, Gary (2002).Introduction to Light: The Physics of Light, Vision, and Color.Courier Corporation. pp. 79–80.ISBN 978-0-486-42118-6.
^Griffiths, David J. (1998).Introduction to Electrodynamics(3rd ed.). Prentice Hall.ISBN 0-13-805326-X.
^Geoffrey New (7 April 2011).Introduction to Nonlinear Optics.Cambridge University Press.ISBN 978-1-139-50076-0.
^Dorn, R.; Quabis, S. & Leuchs, G. (Dec 2003). "Sharper Focus for a Radially Polarized Light Beam".Physical Review Letters.91(23): 233901.Bibcode:2003PhRvL..91w3901D.doi:10.1103/PhysRevLett.91.233901.PMID 14683185.
^Chandrasekhar, Subrahmanyan (1960).Radiative Transfer.Dover. p.27.ISBN 0-486-60590-6.OCLC 924844798.
^^a ^bSletten, Mark A.; Mc Laughlin, David J. (2005-04-15). "Radar Polarimetry". In Chang, Kai (ed.).Encyclopedia of RF and Microwave Engineering.John Wiley & Sons, Inc.doi:10.1002/0471654507.eme343.ISBN 978-0-471-65450-6.
^Schrank, Helmut E.; Evans, Gary E.; Davis, Daniel (1990)."6 Reflector Antennas"(PDF).In Skolnik, Merrill Ivan (ed.).Radar Handbook(PDF).McGraw-Hill. pp. 6.30, Fig 6.25.ISBN 978-0-07-057913-2.Archived(PDF)from the original on 2022-10-09.
^Ishii, T. Koryu, ed. (1995).Handbook of Microwave Technology.Vol. 2: Applications. Elsevier. p. 177.ISBN 978-0-08-053410-7.
^Volakis, John (2007).Antenna Engineering Handbook, Fourth Edition.McGraw-Hill. Sec. 26.1.ISBN 9780071475747:Note:in contrast with other authors, this source initially defines ellipticity reciprocally, as the minor-to-major-axis ratio, but then goes on to say that "Although [it] is less than unity, when expressing ellipticity in decibels, the minus sign is frequently omitted for convenience", which essentially reverts to the definition adopted by other authors.{{cite book}}:CS1 maint: postscript (link)
^Chipman, R.A.; Lam, W.S.T.; Young, G. (2018).Polarized Light and Optical Systems.Optical Sciences and Applications of Light. CRC Press.ISBN 978-1-4987-0057-3.Retrieved2023-01-20.
^Sharma, K.K. (2006).Optics: Principles and Applications.Elsevier Science. p. 145.ISBN 978-0-08-046391-9.Retrieved2023-01-20.
^Prakash, Hari; Chandra, Naresh (1971). "Density Operator of Unpolarized Radiation".Physical Review A.4(2): 796–799.Bibcode:1971PhRvA...4..796P.doi:10.1103/PhysRevA.4.796.
^Chandrasekhar, Subrahmanyan (2013).Radiative transfer.Courier. p. 30.
^^a ^bHecht, Eugene (2002).Optics(4th ed.). United States of America: Addison Wesley.ISBN 0-8053-8566-5.
^Bekefi, George; Barrett, Alan (1977).Electromagnetic Vibrations, Waves, and Radiation.USA: MIT Press.ISBN 0-262-52047-8.
^^a ^b ^cHecht, Eugene (2002).Optics(4th ed.). United States of America: Addison Wesley.ISBN 0-8053-8566-5.
^Dennis Goldstein; Dennis H. Goldstein (3 January 2011).Polarized Light, Revised and Expanded.CRC Press.ISBN 978-0-203-91158-7.
^Masud Mansuripur (2009).Classical Optics and Its Applications.Cambridge University Press.ISBN 978-0-521-88169-2.
^Randy O. Wayne (16 December 2013).Light and Video Microscopy.Academic Press.ISBN 978-0-12-411536-1.
^Peter M. Shearer (2009).Introduction to Seismology.Cambridge University Press.ISBN 978-0-521-88210-1.
^Seth Stein; Michael Wysession (1 April 2009).An Introduction to Seismology, Earthquakes, and Earth Structure.John Wiley & Sons.ISBN 978-1-4443-1131-0.
^Alawi, Faizan; Shields, Bridget E.; Omolehinwa, Temitope; Rosenbach, Misha (2020-10-01)."Oral Granulomatous Disease".Dermatologic Clinics.Oral Medicine in Dermatology.38(4): 429–439.doi:10.1016/j.det.2020.05.004.ISSN 0733-8635.
^Vollhardt, K. Peter C.;Schore, Neil E.(2003).Organic Chemistry: Structure and Function(4th ed.).W. H. Freeman.pp.169–172.ISBN 978-0-7167-4374-3.
^Vlemmings, W. H. T. (Mar 2007)."A review of maser polarization and magnetic fields".Proceedings of the International Astronomical Union.3(S242): 37–46.arXiv:0705.0885.Bibcode:2007IAUS..242...37V.doi:10.1017/s1743921307012549.
^Hannu Karttunen; Pekka Kröger; Heikki Oja (27 June 2007).Fundamental Astronomy.Springer.ISBN 978-3-540-34143-7.
^Boyle, Latham A.; Steinhardt, PJ; Turok, N (2006). "Inflationary predictions for scalar and tensor fluctuations reconsidered".Physical Review Letters.96(11): 111301.arXiv:astro-ph/0507455.Bibcode:2006PhRvL..96k1301B.doi:10.1103/PhysRevLett.96.111301.PMID 16605810.S2CID 10424288.
^Tegmark, Max (2005). "What does inflation really predict?".Journal of Cosmology and Astroparticle Physics.0504(4): 001.arXiv:astro-ph/0410281.Bibcode:2005JCAP...04..001T.doi:10.1088/1475-7516/2005/04/001.S2CID 17250080.
^Clark, S. (1999). "Polarised starlight and the handedness of Life".American Scientist.97(4): 336–43.Bibcode:1999AmSci..87..336C.doi:10.1511/1999.4.336.S2CID 221585816.
^Hazen, Robert M.; Sholl, David S. (2003-06-01)."Chiral selection on inorganic crystalline surfaces".Nature Materials.2(6): 367–374.doi:10.1038/nmat879.ISSN 1476-1122.
^Bekefi, George; Barrett, Alan (1977).Electromagnetic Vibrations, Waves, and Radiation.USA: MIT Press.ISBN 0-262-52047-8.
^^a ^b ^c ^dJ. David Pye (13 February 2001).Polarised Light in Science and Nature.CRC Press.ISBN 978-0-7503-0673-7.
^Sonja Kleinlogel; Andrew White (2008)."The secret world of shrimps: polarisation vision at its best".PLOS ONE.3(5): e2190.arXiv:0804.2162.Bibcode:2008PLoSO...3.2190K.doi:10.1371/journal.pone.0002190.PMC2377063.PMID 18478095.
^Nuboer, J. F. W.; Coemans, M. a. J. M.; Vos Hzn, J. J. (1995-02-01)."No evidence for polarization sensitivity in the pigeon electroretinogram".Journal of Experimental Biology.198(2): 325–335.doi:10.1242/jeb.198.2.325.ISSN 0022-0949.PMID 9317897.Archivedfrom the original on 2019-08-27.Retrieved2019-08-27.
^"'Fastest spinning object' created ".BBC News.2013-08-28.Archivedfrom the original on 2019-09-10.Retrieved2019-08-27.
^Dholakia, Kishan; Mazilu, Michael; Arita, Yoshihiko (August 28, 2013)."Laser-induced rotation and cooling of a trapped microgyroscope in vacuum".Nature Communications.4:2374.Bibcode:2013NatCo...4.2374A.doi:10.1038/ncomms3374.hdl:10023/4019.PMC3763500.PMID 23982323.

General references

Azzam, R. M. A.; Bashara, N. M. (1977).Ellipsometry and Polarized Light.North-Holland.ISBN 0-444-87016-4.
Born, M.; Wolf, E. (1999).Principles of Optics(7th ed.). Cambridge University.ISBN 0-521-64222-1.
Brosseau, C. (1998).Fundamentals of Polarized Light: A Statistical Optics Approach.Wiley.ISBN 0-471-14302-2.
Collett, Edward (2005).Field Guide to Polarization.SPIE Field Guides. Vol. FG05. SPIE.ISBN 0-8194-5868-6.
Damask, Jay N. (2004).Polarization Optics in Telecommunications.Springer.ISBN 0-387-22493-9.
Goldstein, Dennis; Dekker, Marcel (2003).Polarized Light(2nd ed.). Taylor & Francis.ISBN 0-8247-4053-X.
Karlsen, Leif (2003).Secrets of the Viking Navigators: How the Vikings used their amazing sunstones and other techniques to cross the open oceans.One Earth Press.
Können, G. P. (1985).Polarized Light in Nature.Translated by Beerling, G. A. Cambridge University.ISBN 0-521-25862-6.
Pye, David(2001).Polarised Light in Science and Nature.Institute of Physics.ISBN 0-7503-0673-4.
Shurcliff, William A. (1962).Polarized Light, Production and Use.Harvard University.

External links

Feynman's lecture on polarization
Polarized Light Digital Image Gallery:Microscopic images made using polarization effects
MathPages: The relationship between photon spin and polarization
A virtual polarization microscope
Polarization angle in satellite dishes.
Molecular Expressions: Science, Optics and You — Polarization of Light:Interactive Java tutorial
Antenna Polarization
Animations of Linear, Circular and Elliptical Polarizations on YouTube

[Shipman-1] Shipman, James; Wilson, Jerry D.; Higgins, Charles A. (2015).An Introduction to Physical Science, 14th Ed.Cengage Learning. p. 187.ISBN 978-1-305-54467-3.

[Muncaster-2] Muncaster, Roger (1993).A-level Physics.Nelson Thornes. pp. 465–467.ISBN 0-7487-1584-3.

[Singh-3] Singh, Devraj (2015).Fundamentals of Optics, 2nd Ed.PHI Learning Pvt. Ltd. p. 453.ISBN 978-8120351462.

[Avadhanulu-4] Avadhanulu, M. N. (1992).A Textbook of Engineering Physics.S. Chand Publishing. pp. 198–199.ISBN 8121908175.

[Desmarais-5] Desmarais, Louis (1997).Applied Electro Optics.Pearson Education. pp. 162–163.ISBN 0-13-244182-9.

[6] Le Tiec, A.; Novak, J. (July 2016). "Theory of Gravitational Waves".An Overview of Gravitational Waves.pp. 1–41.arXiv:1607.04202.doi:10.1142/9789813141766_0001.ISBN 978-981-314-175-9.S2CID 119283594.

[Lipson-7] Lipson, Stephen G.; Lipson, Henry; Tannhauser, David Stefan (1995).Optical Physics.Cambridge University Press. pp. 125–127.ISBN 978-0-521-43631-1.

[Waldman-8] Waldman, Gary (2002).Introduction to Light: The Physics of Light, Vision, and Color.Courier Corporation. pp. 79–80.ISBN 978-0-486-42118-6.

[Griffiths1998-9] Griffiths, David J. (1998).Introduction to Electrodynamics(3rd ed.). Prentice Hall.ISBN 0-13-805326-X.

[New2011-10] Geoffrey New (7 April 2011).Introduction to Nonlinear Optics.Cambridge University Press.ISBN 978-1-139-50076-0.

[11] Dorn, R.; Quabis, S. & Leuchs, G. (Dec 2003). "Sharper Focus for a Radially Polarized Light Beam".Physical Review Letters.91(23): 233901.Bibcode:2003PhRvL..91w3901D.doi:10.1103/PhysRevLett.91.233901.PMID 14683185.

[12] Chandrasekhar, Subrahmanyan (1960).Radiative Transfer.Dover. p.27.ISBN 0-486-60590-6.OCLC 924844798.

[Stetten-13] Sletten, Mark A.; Mc Laughlin, David J. (2005-04-15). "Radar Polarimetry". In Chang, Kai (ed.).Encyclopedia of RF and Microwave Engineering.John Wiley & Sons, Inc.doi:10.1002/0471654507.eme343.ISBN 978-0-471-65450-6.

[14] Schrank, Helmut E.; Evans, Gary E.; Davis, Daniel (1990)."6 Reflector Antennas"(PDF).In Skolnik, Merrill Ivan (ed.).Radar Handbook(PDF).McGraw-Hill. pp. 6.30, Fig 6.25.ISBN 978-0-07-057913-2.Archived(PDF)from the original on 2022-10-09.

[15] Ishii, T. Koryu, ed. (1995).Handbook of Microwave Technology.Vol. 2: Applications. Elsevier. p. 177.ISBN 978-0-08-053410-7.

[16] Volakis, John (2007).Antenna Engineering Handbook, Fourth Edition.McGraw-Hill. Sec. 26.1.ISBN 9780071475747:Note:in contrast with other authors, this source initially defines ellipticity reciprocally, as the minor-to-major-axis ratio, but then goes on to say that "Although [it] is less than unity, when expressing ellipticity in decibels, the minus sign is frequently omitted for convenience", which essentially reverts to the definition adopted by other authors.{{cite book}}:CS1 maint: postscript (link)

[Unpolarized_light_Chipman_Lam_Young_2018_p.-17] Chipman, R.A.; Lam, W.S.T.; Young, G. (2018).Polarized Light and Optical Systems.Optical Sciences and Applications of Light. CRC Press.ISBN 978-1-4987-0057-3.Retrieved2023-01-20.

[Unpolarized_light_Sharma_2006_p._145-18] Sharma, K.K. (2006).Optics: Principles and Applications.Elsevier Science. p. 145.ISBN 978-0-08-046391-9.Retrieved2023-01-20.

[19] Prakash, Hari; Chandra, Naresh (1971). "Density Operator of Unpolarized Radiation".Physical Review A.4(2): 796–799.Bibcode:1971PhRvA...4..796P.doi:10.1103/PhysRevA.4.796.

[20] Chandrasekhar, Subrahmanyan (2013).Radiative transfer.Courier. p. 30.

[Unpolarized_light_Hecht2002-21] Hecht, Eugene (2002).Optics(4th ed.). United States of America: Addison Wesley.ISBN 0-8053-8566-5.

[Unpolarized_light_Bekefi-22] Bekefi, George; Barrett, Alan (1977).Electromagnetic Vibrations, Waves, and Radiation.USA: MIT Press.ISBN 0-262-52047-8.

[Hecht2002-23] Hecht, Eugene (2002).Optics(4th ed.). United States of America: Addison Wesley.ISBN 0-8053-8566-5.

[GoldsteinGoldstein2011-24] Dennis Goldstein; Dennis H. Goldstein (3 January 2011).Polarized Light, Revised and Expanded.CRC Press.ISBN 978-0-203-91158-7.

[Mansuripur2009-25] Masud Mansuripur (2009).Classical Optics and Its Applications.Cambridge University Press.ISBN 978-0-521-88169-2.

[Wayne2013-26] Randy O. Wayne (16 December 2013).Light and Video Microscopy.Academic Press.ISBN 978-0-12-411536-1.

[Shearer2009-27] Peter M. Shearer (2009).Introduction to Seismology.Cambridge University Press.ISBN 978-0-521-88210-1.

[SteinWysession2009-28] Seth Stein; Michael Wysession (1 April 2009).An Introduction to Seismology, Earthquakes, and Earth Structure.John Wiley & Sons.ISBN 978-1-4443-1131-0.

[29] Alawi, Faizan; Shields, Bridget E.; Omolehinwa, Temitope; Rosenbach, Misha (2020-10-01)."Oral Granulomatous Disease".Dermatologic Clinics.Oral Medicine in Dermatology.38(4): 429–439.doi:10.1016/j.det.2020.05.004.ISSN 0733-8635.

[VollhardtSchore2003-30] Vollhardt, K. Peter C.;Schore, Neil E.(2003).Organic Chemistry: Structure and Function(4th ed.).W. H. Freeman.pp.169–172.ISBN 978-0-7167-4374-3.

[31] Vlemmings, W. H. T. (Mar 2007)."A review of maser polarization and magnetic fields".Proceedings of the International Astronomical Union.3(S242): 37–46.arXiv:0705.0885.Bibcode:2007IAUS..242...37V.doi:10.1017/s1743921307012549.

[KarttunenKröger2007-32] Hannu Karttunen; Pekka Kröger; Heikki Oja (27 June 2007).Fundamental Astronomy.Springer.ISBN 978-3-540-34143-7.

[boyle-33] Boyle, Latham A.; Steinhardt, PJ; Turok, N (2006). "Inflationary predictions for scalar and tensor fluctuations reconsidered".Physical Review Letters.96(11): 111301.arXiv:astro-ph/0507455.Bibcode:2006PhRvL..96k1301B.doi:10.1103/PhysRevLett.96.111301.PMID 16605810.S2CID 10424288.

[tegmark-34] Tegmark, Max (2005). "What does inflation really predict?".Journal of Cosmology and Astroparticle Physics.0504(4): 001.arXiv:astro-ph/0410281.Bibcode:2005JCAP...04..001T.doi:10.1088/1475-7516/2005/04/001.S2CID 17250080.

[35] Clark, S. (1999). "Polarised starlight and the handedness of Life".American Scientist.97(4): 336–43.Bibcode:1999AmSci..87..336C.doi:10.1511/1999.4.336.S2CID 221585816.

[36] Hazen, Robert M.; Sholl, David S. (2003-06-01)."Chiral selection on inorganic crystalline surfaces".Nature Materials.2(6): 367–374.doi:10.1038/nmat879.ISSN 1476-1122.

[Bekefi-37] Bekefi, George; Barrett, Alan (1977).Electromagnetic Vibrations, Waves, and Radiation.USA: MIT Press.ISBN 0-262-52047-8.

[Pye2001-38] J. David Pye (13 February 2001).Polarised Light in Science and Nature.CRC Press.ISBN 978-0-7503-0673-7.

[39] Sonja Kleinlogel; Andrew White (2008)."The secret world of shrimps: polarisation vision at its best".PLOS ONE.3(5): e2190.arXiv:0804.2162.Bibcode:2008PLoSO...3.2190K.doi:10.1371/journal.pone.0002190.PMC2377063.PMID 18478095.

[40] Nuboer, J. F. W.; Coemans, M. a. J. M.; Vos Hzn, J. J. (1995-02-01)."No evidence for polarization sensitivity in the pigeon electroretinogram".Journal of Experimental Biology.198(2): 325–335.doi:10.1242/jeb.198.2.325.ISSN 0022-0949.PMID 9317897.Archivedfrom the original on 2019-08-27.Retrieved2019-08-27.

[41] "'Fastest spinning object' created ".BBC News.2013-08-28.Archivedfrom the original on 2019-09-10.Retrieved2019-08-27.

[42] Dholakia, Kishan; Mazilu, Michael; Arita, Yoshihiko (August 28, 2013)."Laser-induced rotation and cooling of a trapped microgyroscope in vacuum".Nature Communications.4:2374.Bibcode:2013NatCo...4.2374A.doi:10.1038/ncomms3374.hdl:10023/4019.PMC3763500.PMID 23982323.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]