Prosthaphaeresis

Prosthaphaeresis(from the Greekπροσθαφαίρεσις) was analgorithmused in the late 16th century and early 17th century for approximatemultiplicationanddivisionusing formulas fromtrigonometry.For the 25 years preceding the invention of thelogarithmin 1614, it was the only known generally applicable way of approximating products quickly. Its name comes from theGreekprosthen(πρόσθεν) meaning before andaphaeresis(ἀφαίρεσις), meaning taking away or subtraction.

In ancient times the term was used to mean a reduction to bring the apparent place of a moving point or planet to the mean place (seeEquation of the center). Nicholas Copernicusmentions "prosthaphaeresis" several times in his 1543 workDe Revolutionibus Orbium Coelestium,to mean the "great parallax" caused by the displacement of the observer due to the Earth's annual motion.

History and motivation

A spherical triangle

In 16th-century Europe,celestial navigationof ships on long voyages relied heavily onephemeridesto determine their position and course. These voluminous charts prepared byastronomersdetailed the position of stars and planets at various points in time. The models used to compute these were based onspherical trigonometry,which relates the angles andarc lengthsof spherical triangles (see diagram, right) using formulas such as

$\cos a=\cos b\cos c+\sin b\sin c\cos \ Alpha$

and

$\sin b\sin \ Alpha =\sin a\sin \beta,$

wherea,bandcare the anglessubtendedat the centre of the sphere by the corresponding arcs.

When one quantity in such a formula is unknown but the others are known, the unknown quantity can be computed using a series of multiplications, divisions, and trigonometric table lookups. Astronomers had to make thousands of such calculations, and because the best method of multiplication available waslong multiplication,most of this time was spent ta xing ly multiplying out products.

Mathematicians, particularly those who were also astronomers, were looking for an easier way, and trigonometry was one of the most advanced and familiar fields to these people. Prosthaphaeresis appeared in the 1580s, but its originator is not known for certain;its contributors included the mathematiciansIbn Yunis,Johannes Werner,Paul Wittich,Joost Bürgi,Christopher Clavius,andFrançois Viète.Wittich, Ibn Yunis, and Clavius were all astronomers and have all been credited by various sources with discovering the method. Its most well-known proponent wasTycho Brahe,who used it extensively for astronomical calculations such as those described above. It was also used byJohn Napier,who is credited with inventing the logarithms that would supplant it.

The identities

Proof without wordsof the sum-and-difference-to-product cosine identity using anisosceles triangle–xis actually sin asin b

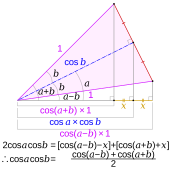
Thetrigonometric identitiesexploited by prosthaphaeresis relate products oftrigonometric functionsto sums. They include the following:

${\begin{aligned}\sin a\sin b&={\frac {\cos(a-b)-\cos(a+b)}{2}}\\[6pt]\cos a\cos b&={\frac {\cos(a-b)+\cos(a+b)}{2}}\\[6pt]\sin a\cos b&={\frac {\sin(a+b)+\sin(a-b)}{2}}\\[6pt]\cos a\sin b&={\frac {\sin(a+b)-\sin(a-b)}{2}}\end{aligned}}$

The first two of these are believed to have been derived byJost Bürgi,who related them to [Tycho?] Brahe;the others follow easily from these two. If both sides are multiplied by 2, these formulas are also called theWerner formulas.

The algorithm

Comparison of logarithm (top) and prosthaphaeresis (bottom) algorithms to multiply two numbers

Using the second formula above, the technique for multiplication of two numbers works as follows:

1. Scale down:By shifting the decimal point to the left or right, scale both numbers to values between$-1$and$1$,to be referred to as$\cos \ Alpha$and$\cos \beta$.
2. Inverse cosine:Using an inverse cosine table, find two angles$\ Alpha$and$\beta$whose cosines are our two values.
3. Sum and difference:Find the sum and difference of the two angles.
4. Average the cosines:Find the cosines of the sum and difference angles using a cosine table and average them, giving (according to the second formula above) the product$\cos \ Alpha \cos \beta$.
5. Scale up:Shift the decimal place in the answer the combined number of places we have shifted the decimal in the first step for each input, but in the opposite direction.

309 →	103× 0.309 →	72°
78.8 →	102× 0.788 →	38°
sum and difference ↓
	−0.342 ←	110°
	0.829 ←	34°
average ↓
24340 ←	103+2× 0.2435

For example, to multiply$309$and$78.8$:

1. Scale down:Shift the decimal point three and two places to the left, respectively. We get$\cos \ Alpha =0.309$and$\cos \beta =0.788$.
2. Inverse cosine:$\arccos 0.309\approx 72^{\circ }$,and$\arccos 0.788\approx 38^{\circ }$.
3. Sum and difference:$72^{\circ }+38^{\circ }=110^{\circ }$,and$72^{\circ }-38^{\circ }=34^{\circ }$.
4. Average the cosines:${\tfrac {1}{2}}(\cos 110^{\circ }+\cos 34^{\circ })$is about${\tfrac {1}{2}}(-0.342+0.829)=0.2435$.
5. Scale up:For each of$105$and$720$we shifted the decimal point a total of five places to the left, so in the answer we shift five places to the right. The result is$24\,350$.This is very close to the actual product,$24\,349.2$(apercent errorof ≈0.003%).

If we want the product of the cosines of the two initial values, which is useful in some of the astronomical calculations mentioned above, this is surprisingly even easier: only steps 3 and 4 above are necessary.

3420 →	104× 0.342 →	70°
1/127 →	1/102× 1/1.27 →	38°
sum and difference ↓
	−0.309 ←	108°
	0.848 ←	32°
average ↓
26.95 ←	104−2× 0.2695

To divide, we exploit the definition of the secant as the reciprocal of the cosine. To divide$3420$by$127$,we scale the numbers to$0.342$and$1.27$.Now$0.342$is the cosine of$70^{\circ }$.Using a table ofsecants,we find$1.27$is the secant of$38^{\circ }$.This means that$1/1.27\approx \cos 38^{\circ }$,and so we can multiply$0.342$by$1/1.27$using the above procedure. Average the cosine of the sum of the angles,$70^{\circ }+38^{\circ }=108^{\circ }$,with the cosine of their difference,$70^{\circ }-38^{\circ }=32^{\circ }$,

${\tfrac {1}{2}}(\cos 108^{\circ }+\cos 32^{\circ })\approx {\tfrac {1}{2}}(-0.309+0.848)=0.2695.$

Scaling up to locate the decimal point gives the approximate answer,$26.95$.

Algorithms using the other formulas are similar, but each using different tables (sine, inverse sine, cosine, and inverse cosine) in different places. The first two are the easiest because they each only require two tables. Using the second formula, however, has the unique advantage that if only a cosine table is available, it can be used to estimate inverse cosines by searching for the angle with the nearest cosine value.

Notice how similar the above algorithm is to the process for multiplying using logarithms, which follows these steps: scale down, take logarithms, add, take inverse logarithm, scale up. It is no surprise that the originators of logarithms had used prosthaphaeresis. Indeed the two are closely related mathematically. In modern terms, prosthaphaeresis can be viewed as relying on the logarithm of complex numbers, in particular onEuler's formula

$e^{ix}=\cos x+i\sin x.$

Decreasing the error

If all the operations are performed with high precision, the product can be as accurate as desired. Although sums, differences, and averages are easy to compute with high precision, even by hand, trigonometric functions and especially inverse trigonometric functions are not. For this reason, the accuracy of the method depends to a large extent on the accuracy and detail of the trigonometric tables used.

For example, a sine table with an entry for each degree can be off by as much as 0.0087 if we justround an angle off to the nearest degree;each time we double the size of the table (for example, by giving entries for every half-degree instead of every degree) we halve this error. Tables were painstakingly constructed for prosthaphaeresis with values for every second, or 3600th of a degree.

Inverse sine and cosine functions are particularly troublesome, because they become steep near −1 and 1. One solution is to include more table values in this area. Another is to scale the inputs to numbers between −0.9 and 0.9. For example, 950 would become 0.095 instead of 0.950.

Another effective approach to enhancing the accuracy islinear interpolation,which chooses a value between two adjacent table values. For example, if we know that the sine of 45° is about 0.707 and the sine of 46° is about 0.719, we can estimate the sine of 45.7° as 0.707 × (1 − 0.7) + 0.719 × 0.7 = 0.7154. The actual sine is 0.7157. A table of cosines with only 180 entries combined with linear interpolation is as accurate as a table with about45000entries without it. Even a quick estimate of the interpolated value is often much closer than the nearest table value. Seelookup tablefor more details.

Reverse identities

The product formulas can also be manipulated to obtain formulas that express addition in terms of multiplication. Although less useful for computing products, these are still useful for deriving trigonometric results:

${\begin{aligned}\sin a+\sin b&=2\sin \left({\frac {a+b}{2}}\right)\cos \left({\frac {a-b}{2}}\right)\\[5pt]\sin a-\sin b&=2\cos \left({\frac {a+b}{2}}\right)\sin \left({\frac {a-b}{2}}\right)\\[5pt]\cos a+\cos b&=2\cos \left({\frac {a+b}{2}}\right)\cos \left({\frac {a-b}{2}}\right)\\[5pt]\cos a-\cos b&=-2\sin \left({\frac {a+b}{2}}\right)\sin \left({\frac {a-b}{2}}\right)\end{aligned}}$

See also

• Slide rule

External links

• Prosthaphaeresis formulas
• Daniel E. OteroHenry BriggsArchived2005-05-22 at theWayback Machine.Introduction: the need for speed in calculation.
• Mathworld: Prosthaphaeresis formulas
• Adam Mosley.Tycho Brahe and Mathematical Techniques.University of Cambridge.
• IEEE Computer Society.History of computing: John Napier and the invention of logarithms.
• Math Words: Prosthaphaeresis
• Beatrice Lumpkin.African and African-American Contributions to MathematicsArchived2020-10-26 at theWayback Machine.Discusses Ibn Yunis's contribution to prosthaphaeresis.
• Prosthaphaeresisand beat phenomenon in the theory of vibrations, by Nicholas J. Rose