Spin (physics)

This article is about the concept in quantum mechanics. For the concept in classical mechanics, seeRotation.

Spinis anintrinsicform ofangular momentumcarried byelementary particles,and thus bycomposite particlessuch ashadrons,atomic nuclei,and atoms.Spin is quantized, and accurate models for the interaction with spin require relativistic quantum mechanics orquantum field theory.

The existence ofelectronspin angular momentumisinferredfrom experiments, such as theStern–Gerlach experiment,in which silver atoms were observed to possess two possible discrete angular momenta despite having no orbital angular momentum.The relativisticspin–statistics theoremconnects electron spin quantization to thePauli exclusion principle:observations of exclusion imply spin and observations of spin imply exclusion.

Spin is described mathematically as a vector for some particles such as photons, and asspinorsandbispinorsfor other particles such as electrons. Spinors and bispinors behave similarly tovectors:they have definite magnitudes and change under rotations; however, they use an unconventional "direction". All elementary particles of a given kind have the same magnitude of spin angular momentum, though its direction may change. These are indicated by assigning the particle aspin quantum number.

TheSI unitsof spin are the same as classical angular momentum (i.e.,N·m·s,J·s, orkg·m²·s⁻¹). In quantum mechanics, angular momentum and spin angular momentum take discrete values proportional to thePlanck constant.In practice, spin is usually given as adimensionlessspin quantum number by dividing the spin angular momentum by thereduced Planck constantħ.Often, the "spin quantum number" is simply called "spin".

Models

Rotating charged mass

The earliest models for electron spin imagined a rotating charged mass, but this model fails when examined in detail: the required space distribution does not match limits on theelectron radius:the required rotation speed exceeds the speed of light.In theStandard Model,the fundamental particles are all considered "point-like": they have their effects through the field that surrounds them.Any model for spin based on mass rotation would need to be consistent with that model.

Pauli's "classically non-describable two-valuedness"

Wolfgang Pauli,a central figure in the history of quantum spin, initially rejected any idea that the "degree of freedom" he introduced to explain experimental observations was related to rotation. He called it "classically non-describable two-valuedness". Later he allowed that it is related to angular momentum, but insisted on considering spin an abstract property.This approach allowed Pauli to develop a proof of his fundamentalPauli exclusion principle,a proof now called thespin-statistics theorem.In retrospect this insistence and the style of his proof initiated the modern particle physics era, where abstract quantum properties derived from symmetry properties dominate. Concrete interpretation became secondary and optional.

Circulation of classical fields

The first classical model for spin proposed small rigid particle rotating about an axis, as ordinary use of the word may suggest. Angular momentum can be computed from a classical field as well.By applyingFrederik Belinfante's approach to calculating the angular momentum of a field, Hans C. Ohanian showed that "spin is essentially a wave property... generated by a circulating flow of charge in the wave field of the electron".This same concept of spin can be applied to gravity waves in water: "spin is generated by subwavelength circular motion of water particles".

Unlike classical wavefield circulation which allows continuous values of angular momentum, quantum wavefields allow only discrete values.Consequently energy transfer to or from spins states always occurs in fixed quantum steps. Only a few steps are allowed: for many qualitative purposes the complexity of the spin quantum wavefields can be ignored and the system properties can be discussed in terms of "integer" or "half-integer" spin models as discussed inquantum numbersbelow.

Dirac's relativistic electron

Quantitative calculations of spin properties for electrons requires the Dirac'srelativistic wave equation.

Relation to orbital angular momentum

As the name suggests, spin was originally conceived as the rotation of a particle around some axis. Historicallyorbital angular momentumrelated to particle orbits.While the names based on mechanical models have survived, the physical explanation has not.Quantizationfundamentally alters the character of both spin and orbital angular momentum.

Since elementary particles are point-like, self-rotation is not well-defined for them. However, spin implies that the phase of the particle depends on the angle as$e^{iS\theta }$,for rotation of angleθaround the axis parallel to the spinS.This is equivalent to the quantum-mechanical interpretation ofmomentumas phase dependence in the position, and oforbital angular momentumas phase dependence in the angular position.

For fermions, the picture is less clear.Angular velocityis equal by theEhrenfest theoremto the derivative of theHamiltonianto itsconjugate momentum,which is the totalangular momentum operatorJ=L+S.Therefore, if the HamiltonianHis dependent upon the spinS,dH/dSis non-zero, and the spin causes angular velocity, and hence actual rotation, i.e. a change in the phase-angle relation over time. However, whether this holds for free electron is ambiguous, since for an electron,S²is constant, and therefore it is a matter of interpretation whether the Hamiltonian includes such a term. Nevertheless, spin appears in theDirac equation,and thus the relativistic Hamiltonian of the electron, treated as aDirac field,can be interpreted as including a dependence in the spinS.

Quantum number

Main article:Spin quantum number

Spin obeys the mathematical laws ofangular momentum quantization.The specific properties of spin angular momenta include:

• Spin quantum numbers may take eitherhalf-integeror integer values.
• Although the direction of its spin can be changed, the magnitude of the spin of an elementary particle cannot be changed.
• The spin of a charged particle is associated with amagnetic dipole momentwith ag-factorthat differs from 1. (In the classical context, this would imply theinternal charge and mass distributions differingfor a rotating object.)

The conventional definition of thespin quantum numberiss=⁠n/2⁠,wherencan be anynon-negative integer.Hence the allowed values ofsare 0,⁠1/2⁠,1,⁠3/2⁠,2, etc. The value ofsfor anelementary particledepends only on the type of particle and cannot be altered in any known way (in contrast to thespin directiondescribed below). The spin angular momentumSof any physical system isquantized.The allowed values ofSare $$S=\hbar \,{\sqrt {s(s+1)}}={\frac {h}{2\pi }}\,{\sqrt {{\frac {n}{2}}{\frac {(n+2)}{2}}}}={\frac {h}{4\pi }}\,{\sqrt {n(n+2)}},$$ wherehis thePlanck constant,and${\textstyle \hbar ={\frac {h}{2\pi }}}$is the reduced Planck constant. In contrast,orbital angular momentumcan only take on integer values ofs;i.e., even-numbered values ofn.

Fermions and bosons

Those particles with half-integer spins, such as⁠1/2⁠,⁠3/2⁠,⁠5/2⁠,are known asfermions,while those particles with integer spins, such as 0, 1, 2, are known asbosons.The two families of particles obey different rules andbroadlyhave different roles in the world around us. A key distinction between the two families is that fermions obey thePauli exclusion principle:that is, there cannot be two identical fermions simultaneously having the same quantum numbers (meaning, roughly, having the same position, velocity and spin direction). Fermions obey the rules ofFermi–Dirac statistics.In contrast, bosons obey the rules ofBose–Einstein statisticsand have no such restriction, so they may "bunch together" in identical states. Also, composite particles can have spins different from their component particles. For example, ahelium-4atom in the ground state has spin 0 and behaves like a boson, even though thequarksand electrons which make it up are all fermions.

This has some profound consequences:

• Quarksandleptons(includingelectronsandneutrinos), which make up what is classically known asmatter,are all fermions withspin⁠1/2⁠.The common idea that "matter takes up space" actually comes from thePauli exclusion principleacting on these particles to prevent the fermions from being in the same quantum state. Further compaction would require electrons to occupy the same energy states, and therefore a kind ofpressure(sometimes known asdegeneracy pressure of electrons) acts to resist the fermions being overly close.
  Elementary fermions with other spins (⁠3/2⁠,⁠5/2⁠,etc.) are not known to exist.
• Elementary particles which are thought of ascarrying forcesare all bosons with spin 1. They include thephoton,which carries theelectromagnetic force,thegluon(strong force), and theW and Z bosons(weak force). The ability of bosons to occupy the same quantum state is used in thelaser,which aligns many photons having the same quantum number (the same direction and frequency),superfluidliquid heliumresulting from helium-4 atoms being bosons, andsuperconductivity,wherepairs of electrons(which individually are fermions) act as single composite bosons.
  Elementary bosons with other spins (0, 2, 3, etc.) were not historically known to exist, although they have received considerable theoretical treatment and are well established within their respective mainstream theories. In particular, theoreticians have proposed thegraviton(predicted to exist by somequantum gravitytheories) with spin 2, and theHiggs boson(explainingelectroweak symmetry breaking) with spin 0. Since 2013, the Higgs boson with spin 0 has been considered proven to exist.It is the firstscalar elementary particle(spin 0) known to exist in nature.
• Atomic nuclei havenuclear spinwhich may be either half-integer or integer, so that the nuclei may be either fermions or bosons.

Spin–statistics theorem

Main article:spin–statistics theorem

Thespin–statistics theoremsplits particles into two groups:bosonsandfermions,where bosons obeyBose–Einstein statistics,and fermions obeyFermi–Dirac statistics(and therefore thePauli exclusion principle). Specifically, the theorem requires that particles with half-integer spins obey thePauli exclusion principlewhile particles with integer spin do not. As an example,electronshave half-integer spin and are fermions that obey the Pauli exclusion principle, while photons have integer spin and do not. The theorem was derived byWolfgang Pauliin 1940; it relies on both quantum mechanics and the theory ofspecial relativity.Pauli described this connection between spin and statistics as "one of the most important applications of the special relativity theory".

Magnetic moments

Schematic diagram depicting the spin of the neutron as the black arrow and magnetic field lines associated with theneutron magnetic moment.The neutron has a negative magnetic moment. While the spin of the neutron is upward in this diagram, the magnetic field lines at the center of the dipole are downward.

Particles with spin can possess amagnetic dipole moment,just like a rotatingelectrically chargedbody inclassical electrodynamics.These magnetic moments can be experimentally observed in several ways, e.g. by the deflection of particles by inhomogeneousmagnetic fieldsin aStern–Gerlach experiment,or by measuring the magnetic fields generated by the particles themselves.

The intrinsic magnetic momentμof aspin-⁠1/2⁠particle with chargeq,massm,and spin angular momentumS,is

${\boldsymbol {\mu }}={\frac {g_{\text{s}}q}{2m}}\mathbf {S},$

where thedimensionless quantityg_sis called the sping-factor.For exclusively orbital rotations it would be 1 (assuming that the mass and the charge occupy spheres of equal radius).

The electron, being a charged elementary particle, possesses anonzero magnetic moment.One of the triumphs of the theory ofquantum electrodynamicsis its accurate prediction of the electrong-factor,which has been experimentally determined to have the value−2.00231930436092(36),with the digits in parentheses denotingmeasurement uncertaintyin the last two digits at onestandard deviation.‍The value of 2 arises from theDirac equation,a fundamental equation connecting the electron's spin with its electromagnetic properties, and thedeviationfrom−2arises from the electron's interaction with the surrounding quantum fields, including its own electromagnetic field and virtual particles.

Composite particles also possess magnetic moments associated with their spin. In particular, theneutronpossesses a non-zero magnetic moment despite being electrically neutral. This fact was an early indication that the neutron is not an elementary particle. In fact, it is made up ofquarks,which are electrically charged particles. Themagnetic moment of the neutroncomes from the spins of the individual quarks and their orbital motions.

Neutrinosare both elementary and electrically neutral. The minimally extendedStandard Modelthat takes into account non-zero neutrino masses predicts neutrino magnetic moments of:

$\mu _{\nu }\approx 3\times 10^{-19}\mu _{\text{B}}{\frac {m_{\nu }c^{2}}{\text{eV}}},$

where theμ_νare the neutrino magnetic moments,m_νare the neutrino masses, andμ_Bis theBohr magneton.New physics above the electroweak scale could, however, lead to significantly higher neutrino magnetic moments. It can be shown in a model-independent way that neutrino magnetic moments larger than about 10⁻¹⁴μ_Bare "unnatural" because they would also lead to large radiative contributions to the neutrino mass. Since the neutrino masses are known to be at most about1 eV/c²,fine-tuningwould be necessary in order to prevent large contributions to the neutrino mass via radiative corrections.The measurement of neutrino magnetic moments is an active area of research. Experimental results have put the neutrino magnetic moment at less than1.2×10⁻¹⁰times the electron's magnetic moment.

On the other hand elementary particles with spin but without electric charge, such as aphotonor aZ boson,do not have a magnetic moment.

Curie temperature and loss of alignment

In ordinary materials, the magnetic dipole moments of individual atoms produce magnetic fields that cancel one another, because each dipole points in a random direction, with the overall average being very near zero.Ferromagneticmaterials below theirCurie temperature,however, exhibitmagnetic domainsin which the atomic dipole moments spontaneously align locally, producing a macroscopic, non-zero magnetic field from the domain. These are the ordinary "magnets" with which we are all familiar.

Inparamagneticmaterials, the magnetic dipole moments of individual atoms will partially align with an externally applied magnetic field. Indiamagneticmaterials, on the other hand, the magnetic dipole moments of individual atoms align oppositely to any externally applied magnetic field, even if it requires energy to do so.

The study of the behavior of such "spin models"is a thriving area of research incondensed matter physics.For instance, theIsing modeldescribes spins (dipoles) that have only two possible states, up and down, whereas in theHeisenberg modelthe spin vector is allowed to point in any direction. These models have many interesting properties, which have led to interesting results in the theory ofphase transitions.

Direction

Further information:Angular momentum operator

Spin projection quantum number and multiplicity

In classical mechanics, the angular momentum of a particle possesses not only a magnitude (how fast the body is rotating), but also a direction (either up or down on theaxis of rotationof the particle). Quantum-mechanical spin also contains information about direction, but in a more subtle form. Quantum mechanics states that thecomponentof angular momentum for a spin-sparticle measured along any direction can only take on the values

$S_{i}=\hbar s_{i},\quad s_{i}\in \{-s,-(s-1),\dots,s-1,s\},$

whereS_iis the spin component along thei-th axis (eitherx,y,orz),s_iis the spin projection quantum number along thei-th axis, andsis the principal spin quantum number (discussed in the previous section). Conventionally the direction chosen is thezaxis:

$S_{z}=\hbar s_{z},\quad s_{z}\in \{-s,-(s-1),\dots,s-1,s\},$

whereS_zis the spin component along thezaxis,s_zis the spin projection quantum number along thezaxis.

One can see that there are2s+ 1possible values ofs_z.The number "2s+ 1"is themultiplicityof the spin system. For example, there are only two possible values for aspin-⁠1/2⁠particle:s_z= +⁠1/2⁠ands_z= −⁠1/2⁠.These correspond toquantum statesin which the spin component is pointing in the +zor −zdirections respectively, and are often referred to as "spin up" and "spin down". For a spin-⁠3/2⁠particle, like adelta baryon,the possible values are +⁠3/2⁠,+⁠1/2⁠,−⁠1/2⁠,−⁠3/2⁠.

Vector

A single point in space can rotate continuously without becoming tangled. Notice that after a 360-degree rotation, the spiral flips between clockwise and counterclockwise orientations. Itreturns to its original configuration after spinning a full 720°.

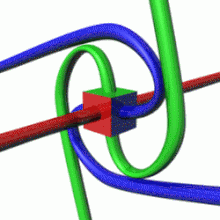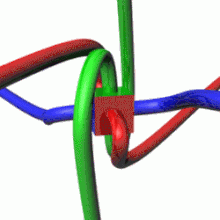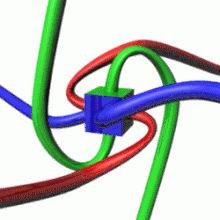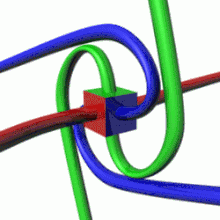
For a givenquantum state,one could think of a spin vector${\textstyle \langle S\rangle }$whose components are theexpectation valuesof the spin components along each axis, i.e.,${\textstyle \langle S\rangle =[\langle S_{x}\rangle,\langle S_{y}\rangle,\langle S_{z}\rangle ]}$.This vector then would describe the "direction" in which the spin is pointing, corresponding to the classical concept of theaxis of rotation.It turns out that the spin vector is not very useful in actual quantum-mechanical calculations, because it cannot be measured directly:s_x,s_yands_zcannot possess simultaneous definite values, because of a quantumuncertainty relationbetween them. However, for statistically large collections of particles that have been placed in the same pure quantum state, such as through the use of aStern–Gerlach apparatus,the spin vector does have a well-defined experimental meaning: It specifies the direction in ordinary space in which a subsequent detector must be oriented in order to achieve the maximum possible probability (100%) of detecting every particle in the collection. For spin-⁠1/2⁠particles, this probability drops off smoothly as the angle between the spin vector and the detector increases, until at an angle of 180°—that is, for detectors oriented in the opposite direction to the spin vector—the expectation of detecting particles from the collection reaches a minimum of 0%.

As a qualitative concept, the spin vector is often handy because it is easy to picture classically. For instance, quantum-mechanical spin can exhibit phenomena analogous to classicalgyroscopic effects.For example, one can exert a kind of "torque"on an electron by putting it in amagnetic field(the field acts upon the electron's intrinsicmagnetic dipole moment—see the following section). The result is that the spin vector undergoesprecession,just like a classical gyroscope. This phenomenon is known aselectron spin resonance(ESR). The equivalent behaviour of protons in atomic nuclei is used innuclear magnetic resonance(NMR) spectroscopy and imaging.

Mathematically, quantum-mechanical spin states are described by vector-like objects known asspinors.There are subtle differences between the behavior of spinors and vectors undercoordinate rotations.For example, rotating a spin-⁠1/2⁠particle by 360° does not bring it back to the same quantum state, but to the state with the opposite quantumphase;this is detectable, in principle, withinterferenceexperiments. To return the particle to its exact original state, one needs a 720° rotation. (Theplate trickandMöbius stripgive non-quantum analogies.) A spin-zero particle can only have a single quantum state, even after torque is applied. Rotating a spin-2 particle 180° can bring it back to the same quantum state, and a spin-4 particle should be rotated 90° to bring it back to the same quantum state. The spin-2 particle can be analogous to a straight stick that looks the same even after it is rotated 180°, and a spin-0 particle can be imagined as sphere, which looks the same after whatever angle it is turned through.

Mathematical formulation

Operator

Spin obeyscommutation relationsanalogous to those of theorbital angular momentum: $$\left[{\hat {S}}_{j},{\hat {S}}_{k}\right]=i\hbar \varepsilon _{jkl}{\hat {S}}_{l},$$ whereε_jklis theLevi-Civita symbol.It follows (as withangular momentum) that theeigenvectorsof${\hat {S}}^{2}$and${\hat {S}}_{z}$(expressed asketsin the totalSbasis) are $${\begin{aligned}{\hat {S}}^{2}|s,m_{s}\rangle &=\hbar ^{2}s(s+1)|s,m_{s}\rangle,\\{\hat {S}}_{z}|s,m_{s}\rangle &=\hbar m_{s}|s,m_{s}\rangle.\end{aligned}}$$

The spinraising and lowering operatorsacting on these eigenvectors give $${\hat {S}}_{\pm }|s,m_{s}\rangle =\hbar {\sqrt {s(s+1)-m_{s}(m_{s}\pm 1)}}|s,m_{s}\pm 1\rangle,$$ where${\hat {S}}_{\pm }={\hat {S}}_{x}\pm i{\hat {S}}_{y}$.

But unlike orbital angular momentum, the eigenvectors are notspherical harmonics.They are not functions ofθandφ.There is also no reason to exclude half-integer values ofsandm_s.

All quantum-mechanical particles possess an intrinsic spin$s$(though this value may be equal to zero). The projection of the spin$s$on any axis is quantized in units of thereduced Planck constant,such that the state function of the particle is, say, not$\psi =\psi (\mathbf {r} )$,but$\psi =\psi (\mathbf {r},s_{z})$,where$s_{z}$can take only the values of the following discrete set: $$s_{z}\in \{-s\hbar,-(s-1)\hbar,\dots,+(s-1)\hbar,+s\hbar \}.$$

One distinguishesbosons(integer spin) andfermions(half-integer spin). The total angular momentum conserved in interaction processes is then the sum of the orbital angular momentum and the spin.

Pauli matrices

Main article:Pauli matrices

Thequantum-mechanical operatorsassociated with spin-⁠1/2⁠observablesare $${\hat {\mathbf {S} }}={\frac {\hbar }{2}}{\boldsymbol {\sigma }},$$ where in Cartesian components $$S_{x}={\frac {\hbar }{2}}\sigma _{x},\quad S_{y}={\frac {\hbar }{2}}\sigma _{y},\quad S_{z}={\frac {\hbar }{2}}\sigma _{z}.$$

For the special case of spin-⁠1/2⁠particles,σ_x,σ_yandσ_zare the threePauli matrices: $$\sigma _{x}={\begin{pmatrix}0&1\\1&0\end{pmatrix}},\quad \sigma _{y}={\begin{pmatrix}0&-i\\i&0\end{pmatrix}},\quad \sigma _{z}={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}.$$

Pauli exclusion principle

ThePauli exclusion principlestates that thewavefunction $\psi (\mathbf {r} _{1},\sigma _{1},\dots,\mathbf {r} _{N},\sigma _{N})$for a system ofNidentical particles having spinsmust change upon interchanges of any two of theNparticles as $$\psi (\dots,\mathbf {r} _{i},\sigma _{i},\dots,\mathbf {r} _{j},\sigma _{j},\dots )=(-1)^{2s}\psi (\dots,\mathbf {r} _{j},\sigma _{j},\dots,\mathbf {r} _{i},\sigma _{i},\dots ).$$

Thus, forbosonsthe prefactor(−1)^2swill reduce to +1, forfermionsto −1. This permutation postulate forN-particle state functions has most important consequences in daily life, e.g. theperiodic tableof the chemical elements.

Rotations

See also:Symmetry in quantum mechanics

As described above, quantum mechanics states thatcomponentsof angular momentum measured along any direction can only take a number of discrete values. The most convenient quantum-mechanical description of particle's spin is therefore with a set of complex numbers corresponding to amplitudes of finding a given value of projection of its intrinsic angular momentum on a given axis. For instance, for a spin-⁠1/2⁠particle, we would need two numbersa_±1/2,giving amplitudes of finding it with projection of angular momentum equal to+⁠ħ/2⁠and−⁠ħ/2⁠,satisfying the requirement $$|a_{+1/2}|^{2}+|a_{-1/2}|^{2}=1.$$

For a generic particle with spins,we would need2s+ 1such parameters. Since these numbers depend on the choice of the axis, they transform into each other non-trivially when this axis is rotated. It is clear that the transformation law must be linear, so we can represent it by associating a matrix with each rotation, and the product of two transformation matrices corresponding to rotations A and B must be equal (up to phase) to the matrix representing rotation AB. Further, rotations preserve the quantum-mechanical inner product, and so should our transformation matrices: $$\sum _{m=-j}^{j}a_{m}^{*}b_{m}=\sum _{m=-j}^{j}\left(\sum _{n=-j}^{j}U_{nm}a_{n}\right)^{*}\left(\sum _{k=-j}^{j}U_{km}b_{k}\right),$$ $$\sum _{n=-j}^{j}\sum _{k=-j}^{j}U_{np}^{*}U_{kq}=\delta _{pq}.$$

Mathematically speaking, these matrices furnish a unitaryprojective representationof therotation group SO(3).Each such representation corresponds to a representation of the covering group of SO(3), which isSU(2).There is onen-dimensional irreducible representation of SU(2) for each dimension, though this representation isn-dimensional real for oddnandn-dimensional complex for evenn(hence of real dimension2n). For a rotation by angleθin the plane with normal vector${\textstyle {\hat {\boldsymbol {\theta }}}}$, $$U=e^{-{\frac {i}{\hbar }}{\boldsymbol {\theta }}\cdot \mathbf {S} },$$ where${\textstyle {\boldsymbol {\theta }}=\theta {\hat {\boldsymbol {\theta }}}}$,andSis the vector ofspin operators.

Proof

Working in the coordinate system where${\textstyle {\hat {\theta }}={\hat {z}}}$,we would like to show thatS_xandS_yare rotated into each other by the angleθ.Starting withS_x.Using units whereħ= 1: $${\begin{aligned}S_{x}\rightarrow U^{\dagger }S_{x}U&=e^{i\theta S_{z}}S_{x}e^{-i\theta S_{z}}\\&=S_{x}+(i\theta )\left[S_{z},S_{x}\right]+\left({\frac {1}{2!}}\right)(i\theta )^{2}\left[S_{z},\left[S_{z},S_{x}\right]\right]+\left({\frac {1}{3!}}\right)(i\theta )^{3}\left[S_{z},\left[S_{z},\left[S_{z},S_{x}\right]\right]\right]+\cdots \end{aligned}}$$

Using thespin operator commutation relations,we see that the commutators evaluate toi S_yfor the odd terms in the series, and toS_xfor all of the even terms. Thus: $${\begin{aligned}U^{\dagger }S_{x}U&=S_{x}\left[1-{\frac {\theta ^{2}}{2!}}+\cdots \right]-S_{y}\left[\theta -{\frac {\theta ^{3}}{3!}}\cdots \right]\\&=S_{x}\cos \theta -S_{y}\sin \theta,\end{aligned}}$$ as expected. Note that since we only relied on the spin operator commutation relations, this proof holds for any dimension (i.e., for any principal spin quantum numbers)

A generic rotation in 3-dimensional space can be built by compounding operators of this type usingEuler angles: $${\mathcal {R}}(\ Alpha,\beta,\gamma )=e^{-i\ Alpha S_{x}}e^{-i\beta S_{y}}e^{-i\gamma S_{z}}.$$

An irreducible representation of this group of operators is furnished by theWigner D-matrix: $$D_{m'm}^{s}(\ Alpha,\beta,\gamma )\equiv \langle sm'|{\mathcal {R}}(\ Alpha,\beta,\gamma )|sm\rangle =e^{-im'\ Alpha }d_{m'm}^{s}(\beta )e^{-im\gamma },$$ where $$d_{m'm}^{s}(\beta )=\langle sm'|e^{-i\beta s_{y}}|sm\rangle$$ isWigner's small d-matrix.Note that forγ= 2πandα=β= 0;i.e., a full rotation about thezaxis, the Wigner D-matrix elements become $$D_{m'm}^{s}(0,0,2\pi )=d_{m'm}^{s}(0)e^{-im2\pi }=\delta _{m'm}(-1)^{2m}.$$

Recalling that a generic spin state can be written as a superposition of states with definitem,we see that ifsis an integer, the values ofmare all integers, and this matrix corresponds to the identity operator. However, ifsis a half-integer, the values ofmare also all half-integers, giving(−1)^2m= −1for allm,and hence upon rotation by 2πthe state picks up a minus sign. This fact is a crucial element of the proof of thespin–statistics theorem.

Lorentz transformations

We could try the same approach to determine the behavior of spin under generalLorentz transformations,but we would immediately discover a major obstacle. Unlike SO(3), the group of Lorentz transformationsSO(3,1)isnon-compactand therefore does not have any faithful, unitary, finite-dimensional representations.

In case of spin-⁠1/2⁠particles, it is possible to find a construction that includes both a finite-dimensional representation and a scalar product that is preserved by this representation. We associate a 4-componentDirac spinorψwith each particle. These spinors transform under Lorentz transformations according to the law $$\psi '=\exp {\left({\tfrac {1}{8}}\ Omega _{\mu \nu }[\gamma _{\mu },\gamma _{\nu }]\right)}\psi,$$ whereγ_νaregamma matrices,andω_μνis an antisymmetric 4 × 4 matrix parametrizing the transformation. It can be shown that the scalar product $$\langle \psi |\phi \rangle ={\bar {\psi }}\phi =\psi ^{\dagger }\gamma _{0}\phi$$ is preserved. It is not, however, positive-definite, so the representation is not unitary.

Measurement of spin along thex,y,orzaxes

Each of the (Hermitian) Pauli matrices of spin-⁠1/2⁠particles has twoeigenvalues,+1 and −1. The correspondingnormalizedeigenvectorsare $${\begin{array}{lclc}\psi _{x+}=\left|{\frac {1}{2}},{\frac {+1}{2}}\right\rangle _{x}=\displaystyle {\frac {1}{\sqrt {2}}}\!\!\!\!\!&{\begin{pmatrix}{1}\\{1}\end{pmatrix}},&\psi _{x-}=\left|{\frac {1}{2}},{\frac {-1}{2}}\right\rangle _{x}=\displaystyle {\frac {1}{\sqrt {2}}}\!\!\!\!\!&{\begin{pmatrix}{1}\\{-1}\end{pmatrix}},\\\psi _{y+}=\left|{\frac {1}{2}},{\frac {+1}{2}}\right\rangle _{y}=\displaystyle {\frac {1}{\sqrt {2}}}\!\!\!\!\!&{\begin{pmatrix}{1}\\{i}\end{pmatrix}},&\psi _{y-}=\left|{\frac {1}{2}},{\frac {-1}{2}}\right\rangle _{y}=\displaystyle {\frac {1}{\sqrt {2}}}\!\!\!\!\!&{\begin{pmatrix}{1}\\{-i}\end{pmatrix}},\\\psi _{z+}=\left|{\frac {1}{2}},{\frac {+1}{2}}\right\rangle _{z}=&{\begin{pmatrix}1\\0\end{pmatrix}},&\psi _{z-}=\left|{\frac {1}{2}},{\frac {-1}{2}}\right\rangle _{z}=&{\begin{pmatrix}0\\1\end{pmatrix}}.\end{array}}$$

(Because any eigenvector multiplied by a constant is still an eigenvector, there is ambiguity about the overall sign. In this article, the convention is chosen to make the first element imaginary and negative if there is a sign ambiguity. The present convention is used by software such asSymPy;while many physics textbooks, such as Sakurai and Griffiths, prefer to make it real and positive.)

By thepostulates of quantum mechanics,an experiment designed to measure the electron spin on thex,y,orzaxis can only yield an eigenvalue of the corresponding spin operator (S_x,S_yorS_z) on that axis, i.e.⁠ħ/2⁠or–⁠ħ/2⁠.Thequantum stateof a particle (with respect to spin), can be represented by a two-componentspinor: $$\psi ={\begin{pmatrix}a+bi\\c+di\end{pmatrix}}.$$

When the spin of this particle is measured with respect to a given axis (in this example, thexaxis), the probability that its spin will be measured as⁠ħ/2⁠is just${\big |}\langle \psi _{x+}|\psi \rangle {\big |}^{2}$.Correspondingly, the probability that its spin will be measured as–⁠ħ/2⁠is just${\big |}\langle \psi _{x-}|\psi \rangle {\big |}^{2}$.Following the measurement, the spin state of the particlecollapsesinto the corresponding eigenstate. As a result, if the particle's spin along a given axis has been measured to have a given eigenvalue, all measurements will yield the same eigenvalue (since${\big |}\langle \psi _{x+}|\psi _{x+}\rangle {\big |}^{2}=1$,etc.), provided that no measurements of the spin are made along other axes.

Measurement of spin along an arbitrary axis

The operator to measure spin along an arbitrary axis direction is easily obtained from the Pauli spin matrices. Letu= (u_x,u_y,u_z)be an arbitrary unit vector. Then the operator for spin in this direction is simply $$S_{u}={\frac {\hbar }{2}}(u_{x}\sigma _{x}+u_{y}\sigma _{y}+u_{z}\sigma _{z}).$$

The operatorS_uhas eigenvalues of±⁠ħ/2⁠,just like the usual spin matrices. This method of finding the operator for spin in an arbitrary direction generalizes to higher spin states, one takes thedot productof the direction with a vector of the three operators for the threex-,y-,z-axis directions.

A normalized spinor for spin-⁠1/2⁠in the(u_x,u_y,u_z)direction (which works for all spin states except spin down, where it will give⁠0/0⁠) is $${\frac {1}{\sqrt {2+2u_{z}}}}{\begin{pmatrix}1+u_{z}\\u_{x}+iu_{y}\end{pmatrix}}.$$

The above spinor is obtained in the usual way by diagonalizing theσ_umatrix and finding the eigenstates corresponding to the eigenvalues. In quantum mechanics, vectors are termed "normalized" when multiplied by a normalizing factor, which results in the vector having a length of unity.

Compatibility of spin measurements

Since the Pauli matrices do notcommute,measurements of spin along the different axes are incompatible. This means that if, for example, we know the spin along thexaxis, and we then measure the spin along theyaxis, we have invalidated our previous knowledge of thexaxis spin. This can be seen from the property of the eigenvectors (i.e. eigenstates) of the Pauli matrices that $${\big |}\langle \psi _{x\pm }|\psi _{y\pm }\rangle {\big |}^{2}={\big |}\langle \psi _{x\pm }|\psi _{z\pm }\rangle {\big |}^{2}={\big |}\langle \psi _{y\pm }|\psi _{z\pm }\rangle {\big |}^{2}={\tfrac {1}{2}}.$$

So whenphysicistsmeasure the spin of a particle along thexaxis as, for example,⁠ħ/2⁠,the particle's spin statecollapsesinto the eigenstate$|\psi _{x+}\rangle$.When we then subsequently measure the particle's spin along theyaxis, the spin state will now collapse into either$|\psi _{y+}\rangle$or$|\psi _{y-}\rangle$,each with probability⁠1/2⁠.Let us say, in our example, that we measure−⁠ħ/2⁠.When we now return to measure the particle's spin along thexaxis again, the probabilities that we will measure⁠ħ/2⁠or−⁠ħ/2⁠are each⁠1/2⁠(i.e. they are${\big |}\langle \psi _{x+}|\psi _{y-}\rangle {\big |}^{2}$and${\big |}\langle \psi _{x-}|\psi _{y-}\rangle {\big |}^{2}$respectively). This implies that the original measurement of the spin along thexaxis is no longer valid, since the spin along thexaxis will now be measured to have either eigenvalue with equal probability.

Higher spins

See also:3D rotation group § A note on Lie algebras

The spin-⁠1/2⁠operatorS=⁠ħ/2⁠σforms thefundamental representationofSU(2).By takingKronecker productsof this representation with itself repeatedly, one may construct all higher irreducible representations. That is, the resultingspin operatorsfor higher-spin systems in three spatial dimensions can be calculated for arbitrarily largesusing thisspin operatorandladder operators.For example, taking the Kronecker product of two spin-⁠1/2⁠yields a four-dimensional representation, which is separable into a 3-dimensional spin-1 (triplet states) and a 1-dimensional spin-0 representation (singlet state).

The resulting irreducible representations yield the following spin matrices and eigenvalues in the z-basis:

1. For spin 1 they are $${\begin{aligned}S_{x}&={\frac {\hbar }{\sqrt {2}}}{\begin{pmatrix}0&1&0\\1&0&1\\0&1&0\end{pmatrix}},&\left|1,+1\right\rangle _{x}&={\frac {1}{2}}{\begin{pmatrix}1\\{\sqrt {2}}\\1\end{pmatrix}},&\left|1,0\right\rangle _{x}&={\frac {1}{\sqrt {2}}}{\begin{pmatrix}-1\\0\\1\end{pmatrix}},&\left|1,-1\right\rangle _{x}&={\frac {1}{2}}{\begin{pmatrix}1\\{-{\sqrt {2}}}\\1\end{pmatrix}}\\S_{y}&={\frac {\hbar }{\sqrt {2}}}{\begin{pmatrix}0&-i&0\\i&0&-i\\0&i&0\end{pmatrix}},&\left|1,+1\right\rangle _{y}&={\frac {1}{2}}{\begin{pmatrix}-1\\-i{\sqrt {2}}\\1\end{pmatrix}},&\left|1,0\right\rangle _{y}&={\frac {1}{\sqrt {2}}}{\begin{pmatrix}1\\0\\1\end{pmatrix}},&\left|1,-1\right\rangle _{y}&={\frac {1}{2}}{\begin{pmatrix}-1\\i{\sqrt {2}}\\1\end{pmatrix}}\\S_{z}&=\hbar {\begin{pmatrix}1&0&0\\0&0&0\\0&0&-1\end{pmatrix}},&\left|1,+1\right\rangle _{z}&={\begin{pmatrix}1\\0\\0\end{pmatrix}},&\left|1,0\right\rangle _{z}&={\begin{pmatrix}0\\1\\0\end{pmatrix}},&\left|1,-1\right\rangle _{z}&={\begin{pmatrix}0\\0\\1\end{pmatrix}}\\\end{aligned}}$$
2. For spin⁠3/2⁠they are $${\begin{array}{lclc}S_{x}={\frac {\hbar }{2}}{\begin{pmatrix}0&{\sqrt {3}}&0&0\\{\sqrt {3}}&0&2&0\\0&2&0&{\sqrt {3}}\\0&0&{\sqrt {3}}&0\end{pmatrix}},\!\!\!&\left|{\frac {3}{2}},{\frac {+3}{2}}\right\rangle _{x}=\!\!\!&{\frac {1}{2{\sqrt {2}}}}{\begin{pmatrix}1\\{\sqrt {3}}\\{\sqrt {3}}\\1\end{pmatrix}},\!\!\!&\left|{\frac {3}{2}},{\frac {+1}{2}}\right\rangle _{x}=\!\!\!&{\frac {1}{2{\sqrt {2}}}}{\begin{pmatrix}{-{\sqrt {3}}}\\-1\\1\\{\sqrt {3}}\end{pmatrix}},\!\!\!&\left|{\frac {3}{2}},{\frac {-1}{2}}\right\rangle _{x}=\!\!\!&{\frac {1}{2{\sqrt {2}}}}{\begin{pmatrix}{\sqrt {3}}\\-1\\-1\\{\sqrt {3}}\end{pmatrix}},\!\!\!&\left|{\frac {3}{2}},{\frac {-3}{2}}\right\rangle _{x}=\!\!\!&{\frac {1}{2{\sqrt {2}}}}{\begin{pmatrix}-1\\{\sqrt {3}}\\{-{\sqrt {3}}}\\1\end{pmatrix}}\\S_{y}={\frac {\hbar }{2}}{\begin{pmatrix}0&-i{\sqrt {3}}&0&0\\i{\sqrt {3}}&0&-2i&0\\0&2i&0&-i{\sqrt {3}}\\0&0&i{\sqrt {3}}&0\end{pmatrix}},\!\!\!&\left|{\frac {3}{2}},{\frac {+3}{2}}\right\rangle _{y}=\!\!\!&{\frac {1}{2{\sqrt {2}}}}{\begin{pmatrix}{i}\\{-{\sqrt {3}}}\\{-i{\sqrt {3}}}\\1\end{pmatrix}},\!\!\!&\left|{\frac {3}{2}},{\frac {+1}{2}}\right\rangle _{y}=\!\!\!&{\frac {1}{2{\sqrt {2}}}}{\begin{pmatrix}{-i{\sqrt {3}}}\\1\\{-i}\\{\sqrt {3}}\end{pmatrix}},\!\!\!&\left|{\frac {3}{2}},{\frac {-1}{2}}\right\rangle _{y}=\!\!\!&{\frac {1}{2{\sqrt {2}}}}{\begin{pmatrix}{i{\sqrt {3}}}\\1\\{i}\\{\sqrt {3}}\end{pmatrix}},\!\!\!&\left|{\frac {3}{2}},{\frac {-3}{2}}\right\rangle _{y}=\!\!\!&{\frac {1}{2{\sqrt {2}}}}{\begin{pmatrix}{-i}\\{-{\sqrt {3}}}\\{i{\sqrt {3}}}\\1\end{pmatrix}}\\S_{z}={\frac {\hbar }{2}}{\begin{pmatrix}3&0&0&0\\0&1&0&0\\0&0&-1&0\\0&0&0&-3\end{pmatrix}},\!\!\!&\left|{\frac {3}{2}},{\frac {+3}{2}}\right\rangle _{z}=\!\!\!&{\begin{pmatrix}1\\0\\0\\0\end{pmatrix}},\!\!\!&\left|{\frac {3}{2}},{\frac {+1}{2}}\right\rangle _{z}=\!\!\!&{\begin{pmatrix}0\\1\\0\\0\end{pmatrix}},\!\!\!&\left|{\frac {3}{2}},{\frac {-1}{2}}\right\rangle _{z}=\!\!\!&{\begin{pmatrix}0\\0\\1\\0\end{pmatrix}},\!\!\!&\left|{\frac {3}{2}},{\frac {-3}{2}}\right\rangle _{z}=\!\!\!&{\begin{pmatrix}0\\0\\0\\1\end{pmatrix}}\\\end{array}}$$
3. For spin⁠5/2⁠they are $${\begin{aligned}{\boldsymbol {S}}_{x}&={\frac {\hbar }{2}}{\begin{pmatrix}0&{\sqrt {5}}&0&0&0&0\\{\sqrt {5}}&0&2{\sqrt {2}}&0&0&0\\0&2{\sqrt {2}}&0&3&0&0\\0&0&3&0&2{\sqrt {2}}&0\\0&0&0&2{\sqrt {2}}&0&{\sqrt {5}}\\0&0&0&0&{\sqrt {5}}&0\end{pmatrix}},\\{\boldsymbol {S}}_{y}&={\frac {\hbar }{2}}{\begin{pmatrix}0&-i{\sqrt {5}}&0&0&0&0\\i{\sqrt {5}}&0&-2i{\sqrt {2}}&0&0&0\\0&2i{\sqrt {2}}&0&-3i&0&0\\0&0&3i&0&-2i{\sqrt {2}}&0\\0&0&0&2i{\sqrt {2}}&0&-i{\sqrt {5}}\\0&0&0&0&i{\sqrt {5}}&0\end{pmatrix}},\\{\boldsymbol {S}}_{z}&={\frac {\hbar }{2}}{\begin{pmatrix}5&0&0&0&0&0\\0&3&0&0&0&0\\0&0&1&0&0&0\\0&0&0&-1&0&0\\0&0&0&0&-3&0\\0&0&0&0&0&-5\end{pmatrix}}.\end{aligned}}$$
4. The generalization of these matrices for arbitrary spinsis $${\begin{aligned}\left(S_{x}\right)_{ab}&={\frac {\hbar }{2}}\left(\delta _{a,b+1}+\delta _{a+1,b}\right){\sqrt {(s+1)(a+b-1)-ab}},\\\left(S_{y}\right)_{ab}&={\frac {i\hbar }{2}}\left(\delta _{a,b+1}-\delta _{a+1,b}\right){\sqrt {(s+1)(a+b-1)-ab}},\\\left(S_{z}\right)_{ab}&=\hbar (s+1-a)\delta _{a,b}=\hbar (s+1-b)\delta _{a,b},\end{aligned}}$$ where indices$a,b$are integer numbers such that $$1\leq a\leq 2s+1,\quad 1\leq b\leq 2s+1.$$

Also useful in thequantum mechanicsof multiparticle systems, the generalPauli groupG_nis defined to consist of alln-foldtensorproducts of Pauli matrices.

The analog formula ofEuler's formula in terms of the Pauli matrices $${\hat {R}}(\theta,{\hat {\mathbf {n} }})=e^{i{\frac {\theta }{2}}{\hat {\mathbf {n} }}\cdot {\boldsymbol {\sigma }}}=I\cos {\frac {\theta }{2}}+i\left({\hat {\mathbf {n} }}\cdot {\boldsymbol {\sigma }}\right)\sin {\frac {\theta }{2}}$$ for higher spins is tractable, but less simple.

Parity

Main article:Parity (physics)

In tables of thespin quantum numbersfor nuclei or particles, the spin is often followed by a "+" or "−".This refers to theparitywith "+" for even parity (wave function unchanged by spatial inversion) and "−" for odd parity (wave function negated by spatial inversion). For example, see theisotopes of bismuth,in which the list of isotopes includes the columnnuclear spinand parity. For Bi-209, the longest-lived isotope, the entry 9/2– means that the nuclear spin is 9/2 and the parity is odd.

Measuring spin

The nuclear spin of atoms can be determined by sophisticated improvements to the originalStern-Gerlach experiment.A single-energy (monochromatic)molecular beamof atoms in an inhomogeneous magnetic field will split into beams representing each possible spin quantum state. For an atom with electronic spinSand nuclear spinI,there are(2S+ 1)(2I+ 1)spin states. For example, neutralNaatoms, which haveS= 1/2,were passed through a series of inhomogeneous magnetic fields that selected one of the two electronic spin states and separated the nuclear spin states, from which four beams were observed. Thus, the nuclear spin for²³Na atoms was found to beI= 3/2.

The spin ofpions,a type of elementary particle, was determined by the principle ofdetailed balanceapplied to those collisions of protons that produced charged pions anddeuterium. $$p+p\rightarrow \pi _{-}+d$$ The known spin values for protons and deuterium allows analysis of the collision cross-section to show that$\pi _{-}$has spin$s_{\pi }=0$.A different approach is needed for neutral pions. In that case the decay reaction into twogamma rayphotons with spin one: $$\pi _{0}\rightarrow 2\gamma$$ This results supplemented with additional analysis leads to the conclusion that the neutral pion also has spin zero.

Applications

Spin has important theoretical implications and practical applications. Well-establisheddirectapplications of spin include:

• Nuclear magnetic resonance(NMR) spectroscopy in chemistry;
• Electron spin resonance(ESR or EPR) spectroscopy in chemistry and physics;
• Magnetic resonance imaging(MRI) in medicine, a type of applied NMR, which relies on proton spin density;
• Giant magnetoresistive(GMR) drive-head technology in modernhard disks.

Electron spin plays an important role inmagnetism,with applications for instance in computer memories. The manipulation ofnuclear spinby radio-frequency waves (nuclear magnetic resonance) is important in chemical spectroscopy and medical imaging.

Spin–orbit couplingleads to thefine structureof atomic spectra, which is used inatomic clocksand in the modern definition of thesecond.Precise measurements of theg-factor of the electron have played an important role in the development and verification ofquantum electrodynamics.Photon spinis associated with thepolarizationof light (photon polarization).

An emerging application of spin is as a binary information carrier inspin transistors.The original concept, proposed in 1990, is known as Datta–Dasspin transistor.Electronics based on spin transistors are referred to asspintronics.The manipulation of spin indilute magnetic semiconductor materials,such as metal-dopedZnOorTiO₂imparts a further degree of freedom and has the potential to facilitate the fabrication of more efficient electronics.

There are manyindirectapplications and manifestations of spin and the associatedPauli exclusion principle,starting with theperiodic tableof chemistry.

History

See also:History of quantum mechanics

Wolfgang Paulilecturing

Spin was first discovered in the context of theemission spectrumofalkali metals.Starting around 1910, many experiments on different atoms produced a collection of relationships involvingquantum numbersfor atomic energy levels partially summarized inBohr's model for the atomTransitions between levels obeyedselection rulesand the rules were known to be correlated with even or oddatomic number.Additional information was known from changes to atomic spectra observed in strong magnetic fields, known as theZeeman effect.In 1924,Wolfgang Pauliused this large collection of empirical observations to propose a new degree of freedom,introducing what he called a "two-valuedness not describable classically"associated with the electron in the outermostshell.

The physical interpretation of Pauli's "degree of freedom" was initially unknown.Ralph Kronig,one ofAlfred Landé's assistants, suggested in early 1925 that it was produced by the self-rotation of the electron. When Pauli heard about the idea, he criticized it severely, noting that the electron's hypothetical surface would have to be moving faster than thespeed of lightin order for it to rotate quickly enough to produce the necessary angular momentum. This would violate thetheory of relativity.Largely due to Pauli's criticism, Kronig decided not to publish his idea.

In the autumn of 1925, the same thought came to Dutch physicistsGeorge UhlenbeckandSamuel GoudsmitatLeiden University.Under the advice ofPaul Ehrenfest,they published their results.The young physicists immediately regretted the publication:Hendrik LorentzandWerner Heisenbergboth pointed out problems with the concept of a spinning electron.

Pauli was especially unconvinced and continued to pursue his two-valued degree of freedom. This allowed him to formulate thePauli exclusion principle,stating that no two electrons can have the samequantum statein the same quantum system.

Fortunately by February 1926Llewellyn Thomasmanaged to resolve a factor-of-two discrepancy between experimental results for thefine structurein the hydrogen spectrum and calculations based on Uhlenbeck and Goudsmit's (and Kronig's unpublished) model.This discrepancy was due to a relativistic effect, the difference between the electron's rotating rest frame and the nuclear rest frame; the effect is now known asThomas precession.Thomas' result convinced Pauli that electron spin was the correct interpretation of his two-valued degree of freedom, while he continued to insist that the classical rotating charge model is invalid.

In 1927 Pauli formalized the theory of spin using the theory of quantum mechanics invented byErwin SchrödingerandWerner Heisenberg.He pioneered the use ofPauli matricesas arepresentationof the spin operators and introduced a two-componentspinorwave-function.

Pauli's theory of spin was non-relativistic. In 1928,Paul Diracpublished his relativistic electron equation, using a four-component spinor (known as a "Dirac spinor") for the electron wave-function. Relativistic spin explained gyromagnetic anomaly. In 1940, Pauli proved thespin–statistics theorem,which states thatfermionshave half-integer spin, andbosonshave integer spin.

In retrospect, the first direct experimental evidence of the electron spin was theStern–Gerlach experimentof 1922. However, the correct explanation of this experiment was only given in 1927. The original interpretation assumed the two spots observed in the experiment were due to quantizedorbital angular momentum.However, in 1927 Ronald Fraser showed that Sodium atoms are isotropic with no orbital angular momentum and suggested that the observed magnetic properties were due to electron spin.In same year, Phipps and Taylor applied the Stern-Gerlach technique to hydrogen atoms; the ground state of hydrogen has zero angular momentum but the measurements again showed two peaks. Once the quantum theory became established, it became clear that the original interpretation could not have been correct: the possible values of orbital angular momentum along one axis is always an odd number, unlike the observations. Hydrogen atoms have a single electron with two spin states giving the two spots observed; silver atoms have closed shells which do not contribute to the magnetic moment and only the unmatched outer electron's spin responds to the field.

See also

• Chirality (physics)
• Dynamic nuclear polarization
• Helicity (particle physics)
• Holstein–Primakoff transformation
• Kramers' theorem
• Pauli equation
• Pauli–Lubanski pseudovector
• Rarita–Schwinger equation
• Representation theory of SU(2)
• Spin angular momentum of light
• Spin engineering
• Spin-flip
• Spin isomers of hydrogen
• Spin–orbit interaction
• Spin tensor
• Spintronics
• Spin wave
• Yrast

Further reading

• Cohen-Tannoudji, Claude; Diu, Bernard; Laloë, Franck (2006).Quantum Mechanics(2 volume set ed.). John Wiley & Sons.ISBN978-0-471-56952-7.
• Condon, E. U.; Shortley, G. H. (1935). "Especially Chapter 3".The Theory of Atomic Spectra.Cambridge University Press.ISBN978-0-521-09209-8.
• Hipple, J. A.; Sommer, H.; Thomas, H.A. (1949)."A precise method of determining the faraday by magnetic resonance".Physical Review.76(12): 1877–1878.Bibcode:1949PhRv...76.1877H.doi:10.1103/PhysRev.76.1877.2.
• Edmonds, A. R. (1957).Angular Momentum in Quantum Mechanics.Princeton University Press.ISBN978-0-691-07912-7.
• Jackson, John David (1998).Classical Electrodynamics(3rd ed.). John Wiley & Sons.ISBN978-0-471-30932-1.
• Serway, Raymond A.; Jewett, John W. (2004).Physics for Scientists and Engineers(6th ed.). Brooks/Cole.ISBN978-0-534-40842-8.
• Thompson, William J. (1994).Angular Momentum: An Illustrated Guide to Rotational Symmetries for Physical Systems.Wiley.ISBN978-0-471-55264-2.
• Tipler, Paul (2004).Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics(5th ed.). W. H. Freeman.ISBN978-0-7167-0809-4.
• Sin-Itiro Tomonaga, The Story of Spin, 1997

External links

• Quotations related toSpin (physics)at Wikiquote
• Goudsmit on the discovery of electron spin.
• Nature:"Milestones in 'spin' since 1896."
• ECE 495N Lecture 36: SpinOnline lecture by S. Datta