Square root of 2

"Pythagoras's constant" redirects here. Not to be confused withPythagoras number.

Square root of 2

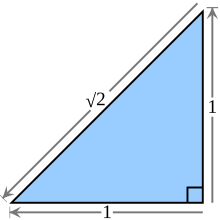The square root of 2 is equal to the length of thehypotenuseof anisoscelesright trianglewith legs of length 1.
Representations
Decimal	1.4142135623730950488...
Continued fraction	$1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ddots }}}}}}}}$

Thesquare root of 2(approximately 1.4142) is a positivereal numberthat, when multiplied by itself or squared, equals thenumber 2.It may be written in mathematics as${\sqrt {2}}$or$2^{1/2}$.It is analgebraic number,and therefore not atranscendental number.Technically, it should be called theprincipalsquare rootof 2, to distinguish it from the negative number with the same property.

Geometrically, the square root of 2 is the length of a diagonal across asquare with sides of one unit of length;this follows from thePythagorean theorem.It was probably the first number known to beirrational.The fraction⁠99/70⁠(≈1.4142857) is sometimes used as a goodrational approximationwith a reasonably smalldenominator.

SequenceA002193in theOn-Line Encyclopedia of Integer Sequencesconsists of the digits in thedecimal expansionof the square root of 2, here truncated to 65 decimal places:

1.41421356237309504880168872420969807856967187537694807317667973799

History

Babylonian clay tabletYBC 7289with annotations. Besides showing the square root of 2 insexagesimal(1 24 51 10), the tablet also gives an example where one side of the square is 30 and the diagonal then is42 25 35.The sexagesimal digit 30 can also stand for0 30=⁠1/2⁠,in which case0 42 25 35is approximately 0.7071065.

TheBabylonianclay tabletYBC 7289(c. 1800–1600 BC) gives an approximation of${\sqrt {2}}$in foursexagesimalfigures,1 24 51 10,which is accurate to about sixdecimaldigits,and is the closest possible three-place sexagesimal representation of${\sqrt {2}}$,representing a margin of error of only –0.000042%:

$1+{\frac {24}{60}}+{\frac {51}{60^{2}}}+{\frac {10}{60^{3}}}={\frac {305470}{216000}}=1.41421{\overline {296}}.$

Another early approximation is given inancient Indianmathematical texts, theSulbasutras(c. 800–200 BC), as follows:Increase the length [of the side] by its third and this third by its own fourth less the thirty-fourth part of that fourth.That is,

$1+{\frac {1}{3}}+{\frac {1}{3\times 4}}-{\frac {1}{3\times 4\times 34}}={\frac {577}{408}}=1.41421{\overline {56862745098039}}.$

This approximation, diverging from the actual value of${\sqrt {2}}$by approximately +0.07%, is the seventh in a sequence of increasingly accurate approximations based on the sequence ofPell numbers,which can be derived from thecontinued fractionexpansion of${\sqrt {2}}$.Despite having a smaller denominator, it is only slightly less accurate than the Babylonian approximation.

Pythagoreansdiscovered that the diagonal of asquareis incommensurable with its side, or in modern language, that the square root of two isirrational.Little is known with certainty about the time or circumstances of this discovery, but the name ofHippasusof Metapontum is often mentioned. For a while, the Pythagoreans treated as an official secret the discovery that the square root of two is irrational, and, according to legend, Hippasus was murdered for divulging it, though this has little to any substantial evidence in traditional historian practice.The square root of two is occasionally calledPythagoras's numberorPythagoras's constant.

Ancient Roman architecture

Inancient Roman architecture,Vitruviusdescribes the use of the square root of 2 progression orad quadratumtechnique. It consists basically in a geometric, rather than arithmetic, method to double a square, in which the diagonal of the original square is equal to the side of the resulting square. Vitruvius attributes the idea toPlato.The system was employed to build pavements by creating a squaretangentto the corners of the original square at 45 degrees of it. The proportion was also used to designatriaby giving them a length equal to a diagonal taken from a square, whose sides are equivalent to the intended atrium's width.

Decimal value

Computation algorithms

Further information:Methods of computing square roots

There are manyalgorithmsfor approximating${\sqrt {2}}$as a ratio ofintegersor as a decimal. The most common algorithm for this, which is used as a basis in many computers and calculators, is theBabylonian methodfor computing square roots, an example ofNewton's methodfor computing roots of arbitrary functions. It goes as follows:

First, pick a guess,$a_{0}>0$;the value of the guess affects only how many iterations are required to reach an approximation of a certain accuracy. Then, using that guess, iterate through the followingrecursivecomputation:

$a_{n+1}={\frac {1}{2}}\left(a_{n}+{\dfrac {2}{a_{n}}}\right)={\frac {a_{n}}{2}}+{\frac {1}{a_{n}}}.$

Each iteration improves the approximation, roughly doubling the number of correct digits. Starting with$a_{0}=1$,the subsequent iterations yield:

${\begin{alignedat}{3}a_{1}&={\tfrac {3}{2}}&&=\mathbf {1}.5,\\[3mu]a_{2}&={\tfrac {17}{12}}&&=\mathbf {1.41} 6\ldots,\\[3mu]a_{3}&={\tfrac {577}{408}}&&=\mathbf {1.41421} 5\ldots,\\[3mu]a_{4}&={\tfrac {665857}{470832}}&&=\mathbf {1.41421356237} 46\ldots,\\[3mu]&\qquad \vdots \end{alignedat}}$

Rational approximations

A simple rational approximation⁠99/70⁠(≈1.4142857) is sometimes used. Despite having a denominator of only 70, it differs from the correct value by less than⁠1/10,000⁠(approx.+0.72×10⁻⁴).

The next two better rational approximations are⁠140/99⁠(≈1.4141414...) with a marginally smaller error (approx.−0.72×10⁻⁴), and⁠239/169⁠(≈1.4142012) with an error of approx−0.12×10⁻⁴.

The rational approximation of the square root of two derived from four iterations of the Babylonian method after starting witha₀= 1(⁠665,857/470,832⁠) is too large by about1.6×10⁻¹²;its square is ≈ 2.0000000000045.

Records in computation

In 1997, the value of${\sqrt {2}}$was calculated to 137,438,953,444 decimal places byYasumasa Kanada's team. In February 2006, the record for the calculation of${\sqrt {2}}$was eclipsed with the use of a home computer. Shigeru Kondo calculated onetrilliondecimal places in 2010.Othermathematical constantswhose decimal expansions have been calculated to similarly high precision includeπ,e,and thegolden ratio.Such computations aim to check empirically whether such numbers arenormal.

This is a table of recent records in calculating the digits of${\sqrt {2}}$.

Date	Name	Number of digits
January 5, 2022	Tizian Hanselmann	10000000001000
June 28, 2016	Ron Watkins	10000000000000
April 3, 2016	Ron Watkins	5000000000000
January 20, 2016	Ron Watkins	2000000000100
February 9, 2012	Alexander Yee	2000000000050
March 22, 2010	Shigeru Kondo	1000000000000

Proofs of irrationality

Proof by infinite descent

One proof of the number's irrationality is the followingproof by infinite descent.It is also aproof of a negation by refutation:it proves the statement "${\sqrt {2}}$is not rational "by assuming that it is rational and then deriving a falsehood.

1. Assume that${\sqrt {2}}$is a rational number, meaning that there exists a pair of integers whose ratio is exactly${\sqrt {2}}$.
2. If the two integers have a commonfactor,it can be eliminated using theEuclidean algorithm.
3. Then${\sqrt {2}}$can be written as anirreducible fraction${\frac {a}{b}}$such thataandbarecoprime integers(having no common factor) which additionally means that at least one ofaorbmust beodd.
4. It follows that${\frac {a^{2}}{b^{2}}}=2$and$a^{2}=2b^{2}$.  ( (⁠a/b⁠)ⁿ=⁠aⁿ/bⁿ⁠ )   (a²andb²are integers)
5. Therefore,a²isevenbecause it is equal to2b².(2b²is necessarily even because it is 2 times another whole number.)
6. It follows thatamust be even (as squares of odd integers are never even).
7. Becauseais even, there exists an integerkthat fulfills$a=2k$.
8. Substituting2kfrom step 7 forain the second equation of step 4:$2b^{2}=a^{2}=(2k)^{2}=4k^{2}$,which is equivalent to$b^{2}=2k^{2}$.
9. Because2k²is divisible by two and therefore even, and because$2k^{2}=b^{2}$,it follows thatb²is also even which means thatbis even.
10. By steps 5 and 8,aandbare both even, which contradicts step 3 (that${\frac {a}{b}}$is irreducible).

Since we have derived a falsehood, the assumption (1) that${\sqrt {2}}$is a rational number must be false. This means that${\sqrt {2}}$is not a rational number; that is to say,${\sqrt {2}}$is irrational.

This proof was hinted at byAristotle,in hisAnalytica Priora,§I.23.It appeared first as a full proof inEuclid'sElements,as proposition 117 of Book X. However, since the early 19th century, historians have agreed that this proof is aninterpolationand not attributable to Euclid.

Proof by unique factorization

As with the proof by infinite descent, we obtain$a^{2}=2b^{2}$.Being the same quantity, each side has the sameprime factorizationby thefundamental theorem of arithmetic,and in particular, would have to have the factor 2 occur the same number of times. However, the factor 2 appears an odd number of times on the right, but an even number of times on the left—a contradiction.

Application of the rational root theorem

The irrationality of${\sqrt {2}}$also follows from therational root theorem,which states that a rationalrootof apolynomial,if it exists, must be thequotientof a factor of the constant term and a factor of theleading coefficient.In the case of$p(x)=x^{2}-2$,the only possible rational roots are$\pm 1$and$\pm 2$.As${\sqrt {2}}$is not equal to$\pm 1$or$\pm 2$,it follows that${\sqrt {2}}$is irrational. This application also invokes the integer root theorem, a stronger version of the rational root theorem for the case when$p(x)$is amonic polynomialwith integercoefficients;for such a polynomial, all roots are necessarily integers (which${\sqrt {2}}$is not, as 2 is not a perfect square) or irrational.

The rational root theorem (or integer root theorem) may be used to show that any square root of anynatural numberthat is not a perfect square is irrational. For other proofs that the square root of any non-square natural number is irrational, seeQuadratic irrational numberorInfinite descent.

Geometric proof

Figure 1. Stanley Tennenbaum's geometric proof of theirrationalityof√2

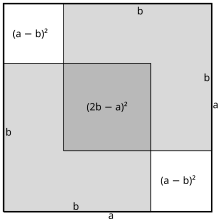
A simple proof is attributed toStanley Tennenbaumwhen he was a student in the early 1950s.Given two squares with integer sides respectivelyaandb,one of which has twice theareaof the other, place two copies of the smaller square in the larger as shown in Figure 1. The square overlap region in the middle ($(2b-a)^{2}$) must equal the sum of the two uncovered squares ($2(a-b)^{2}$). However, these squares on the diagonal have positive integer sides that are smaller than the original squares. Repeating this process, there are arbitrarily small squares one twice the area of the other, yet both having positive integer sides, which is impossible since positive integers cannot be less than 1.

Figure 2. Tom Apostol's geometric proof of the irrationality of√2

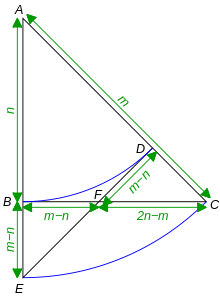
Tom M. Apostolmade another geometricreductio ad absurdumargument showing that${\sqrt {2}}$is irrational.It is also an example of proof by infinite descent. It makes use of classiccompass and straightedgeconstruction, proving the theorem by a method similar to that employed by ancient Greek geometers. It is essentially the same algebraic proof as in the previous paragraph, viewed geometrically in another way.

Let△ ABCbe a right isosceles triangle with hypotenuse lengthmand legsnas shown in Figure 2. By thePythagorean theorem,${\frac {m}{n}}={\sqrt {2}}$.Supposemandnare integers. Letm:nbe aratiogiven in itslowest terms.

Draw the arcsBDandCEwith centreA.JoinDE.It follows thatAB=AD,AC=AEand∠BACand∠DAEcoincide. Therefore, thetrianglesABCandADEarecongruentbySAS.

Because∠EBFis a right angle and∠BEFis half a right angle,△ BEFis also a right isosceles triangle. HenceBE=m−nimpliesBF=m−n.By symmetry,DF=m−n,and△ FDCis also a right isosceles triangle. It also follows thatFC=n− (m−n) = 2n−m.

Hence, there is an even smaller right isosceles triangle, with hypotenuse length2n−mand legsm−n.These values are integers even smaller thanmandnand in the same ratio, contradicting the hypothesis thatm:nis in lowest terms. Therefore,mandncannot be both integers; hence,${\sqrt {2}}$is irrational.

Constructive proof

While the proofs by infinite descent are constructively valid when "irrational" is defined to mean "not rational", we can obtain a constructively stronger statement by using a positive definition of "irrational" as "quantifiably apart from every rational". Letaandbbe positive integers such that1<⁠a/b⁠< 3/2(as1<2< 9/4satisfies these bounds). Now2b²anda²cannot be equal, since the first has an odd number of factors 2 whereas the second has an even number of factors 2. Thus|2b²−a²| ≥ 1.Multiplying the absolute difference|√2−⁠a/b⁠|byb²(√2+⁠a/b⁠)in the numerator and denominator, we get

$\left|{\sqrt {2}}-{\frac {a}{b}}\right|={\frac {|2b^{2}-a^{2}|}{b^{2}\!\left({\sqrt {2}}+{\frac {a}{b}}\right)}}\geq {\frac {1}{b^{2}\!\left({\sqrt {2}}+{\frac {a}{b}}\right)}}\geq {\frac {1}{3b^{2}}},$

the latterinequalitybeing true because it is assumed that1<⁠a/b⁠< 3/2,giving⁠a/b⁠+√2≤ 3(otherwise the quantitative apartness can be trivially established). This gives a lower bound of⁠1/3b²⁠for the difference|√2−⁠a/b⁠|,yielding a direct proof of irrationality in its constructively stronger form, not relying on thelaw of excluded middle;seeErrett Bishop(1985, p. 18). This proof constructively exhibits an explicit discrepancy between${\sqrt {2}}$and any rational.

Proof by Pythagorean triples

This proof uses the following property of primitivePythagorean triples:

Ifa,b,andcare coprime positive integers such thata²+b²=c²,thencis never even.

This lemma can be used to show that two identical perfect squares can never be added to produce another perfect square.

Suppose the contrary that${\sqrt {2}}$is rational. Therefore,

${\sqrt {2}}={a \over b}$

where$a,b\in \mathbb {Z}$and$\gcd(a,b)=1$

Squaring both sides,

$2={a^{2} \over b^{2}}$

$2b^{2}=a^{2}$

$b^{2}+b^{2}=a^{2}$

Here,(b, b, a)is a primitive Pythagorean triple, and from the lemmaais never even. However, this contradicts the equation2b²=a²which implies thatamust be even.

Multiplicative inverse

Themultiplicative inverse(reciprocal) of the square root of two (i.e., the square root of⁠1/2⁠) is a widely usedconstant.

${\frac {1}{\sqrt {2}}}={\frac {\sqrt {2}}{2}}=\sin 45^{\circ }=\cos 45^{\circ }=$0.70710678118654752440084436210484903928483593768847... (sequenceA010503in theOEIS)

One-half of${\sqrt {2}}$,also the reciprocal of${\sqrt {2}}$,is a common quantity ingeometryandtrigonometrybecause theunit vectorthat makes a 45°anglewith the axes in a plane has the coordinates

$\left({\frac {\sqrt {2}}{2}},{\frac {\sqrt {2}}{2}}\right)\!.$

This number satisfies

${\tfrac {1}{2}}{\sqrt {2}}={\sqrt {\tfrac {1}{2}}}={\frac {1}{\sqrt {2}}}=\cos 45^{\circ }=\sin 45^{\circ }.$

Properties

Anglesize and sectorareaare the same when the conic radius is√2.This diagram illustrates the circular and hyperbolic functions based on sector areasu.

One interesting property of${\sqrt {2}}$is

$\!\ {1 \over {{\sqrt {2}}-1}}={\sqrt {2}}+1$

since

$\left({\sqrt {2}}+1\right)\!\left({\sqrt {2}}-1\right)=2-1=1.$

This is related to the property ofsilver ratios.

${\sqrt {2}}$can also be expressed in terms of copies of theimaginary unitiusing only thesquare rootandarithmetic operations,if the square root symbol is interpreted suitably for thecomplex numbersiand−i:

${\frac {{\sqrt {i}}+i{\sqrt {i}}}{i}}{\text{ and }}{\frac {{\sqrt {-i}}-i{\sqrt {-i}}}{-i}}$

${\sqrt {2}}$is also the only real number other than 1 whose infinitetetrate(i.e., infinite exponential tower) is equal to its square. In other words: if forc> 1,x₁=candx_n+1=c^x_nforn> 1,thelimitofx_nasn→ ∞will be called (if this limit exists)f(c).Then${\sqrt {2}}$is the only numberc> 1for whichf(c) =c².Or symbolically:

${\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{~\cdot ^{~\cdot ^{~\cdot }}}}}=2.$

${\sqrt {2}}$appears inViète's formulaforπ,

${\frac {2}{\pi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}}}\cdots,$

which is related to the formula

$\pi =\lim _{m\to \infty }2^{m}\underbrace {\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2+\cdots +{\sqrt {2}}}}}}}}}} _{m{\text{ square roots}}}\,.$

Similar in appearance but with a finite number of terms,${\sqrt {2}}$appears in varioustrigonometric constants:

${\begin{aligned}\sin {\frac {\pi }{32}}&={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}}&\quad \sin {\frac {3\pi }{16}}&={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2-{\sqrt {2}}}}}}&\quad \sin {\frac {11\pi }{32}}&={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2-{\sqrt {2-{\sqrt {2}}}}}}}}\\[6pt]\sin {\frac {\pi }{16}}&={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {2}}}}}}&\quad \sin {\frac {7\pi }{32}}&={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2-{\sqrt {2+{\sqrt {2}}}}}}}}&\quad \sin {\frac {3\pi }{8}}&={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2}}}}\\[6pt]\sin {\frac {3\pi }{32}}&={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {2-{\sqrt {2}}}}}}}}&\quad \sin {\frac {\pi }{4}}&={\tfrac {1}{2}}{\sqrt {2}}&\quad \sin {\frac {13\pi }{32}}&={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {2-{\sqrt {2}}}}}}}}\\[6pt]\sin {\frac {\pi }{8}}&={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2}}}}&\quad \sin {\frac {9\pi }{32}}&={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2-{\sqrt {2+{\sqrt {2}}}}}}}}&\quad \sin {\frac {7\pi }{16}}&={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}\\[6pt]\sin {\frac {5\pi }{32}}&={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2-{\sqrt {2-{\sqrt {2}}}}}}}}&\quad \sin {\frac {5\pi }{16}}&={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2-{\sqrt {2}}}}}}&\quad \sin {\frac {15\pi }{32}}&={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}}\end{aligned}}$

It is not known whether${\sqrt {2}}$is anormal number,which is a stronger property than irrationality, but statistical analyses of itsbinary expansionare consistent with the hypothesis that it is normal tobase two.

Representations

Series and product

The identitycos ⁠π/4⁠= sin ⁠π/4⁠=⁠1/√2⁠,along with the infinite product representations for thesine and cosine,leads to products such as

${\frac {1}{\sqrt {2}}}=\prod _{k=0}^{\infty }\left(1-{\frac {1}{(4k+2)^{2}}}\right)=\left(1-{\frac {1}{4}}\right)\!\left(1-{\frac {1}{36}}\right)\!\left(1-{\frac {1}{100}}\right)\cdots$

and

${\sqrt {2}}=\prod _{k=0}^{\infty }{\frac {(4k+2)^{2}}{(4k+1)(4k+3)}}=\left({\frac {2\cdot 2}{1\cdot 3}}\right)\!\left({\frac {6\cdot 6}{5\cdot 7}}\right)\!\left({\frac {10\cdot 10}{9\cdot 11}}\right)\!\left({\frac {14\cdot 14}{13\cdot 15}}\right)\cdots$

or equivalently,

${\sqrt {2}}=\prod _{k=0}^{\infty }\left(1+{\frac {1}{4k+1}}\right)\left(1-{\frac {1}{4k+3}}\right)=\left(1+{\frac {1}{1}}\right)\!\left(1-{\frac {1}{3}}\right)\!\left(1+{\frac {1}{5}}\right)\!\left(1-{\frac {1}{7}}\right)\cdots.$

The number can also be expressed by taking theTaylor seriesof atrigonometric function.For example, the series forcos ⁠π/4⁠gives

${\frac {1}{\sqrt {2}}}=\sum _{k=0}^{\infty }{\frac {(-1)^{k}\left({\frac {\pi }{4}}\right)^{2k}}{(2k)!}}.$

The Taylor series of√1 +xwithx= 1and using thedouble factorialn!!gives

${\sqrt {2}}=\sum _{k=0}^{\infty }(-1)^{k+1}{\frac {(2k-3)!!}{(2k)!!}}=1+{\frac {1}{2}}-{\frac {1}{2\cdot 4}}+{\frac {1\cdot 3}{2\cdot 4\cdot 6}}-{\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6\cdot 8}}+\cdots =1+{\frac {1}{2}}-{\frac {1}{8}}+{\frac {1}{16}}-{\frac {5}{128}}+{\frac {7}{256}}+\cdots.$

Theconvergenceof this series can be accelerated with anEuler transform,producing

${\sqrt {2}}=\sum _{k=0}^{\infty }{\frac {(2k+1)!}{2^{3k+1}(k!)^{2}}}={\frac {1}{2}}+{\frac {3}{8}}+{\frac {15}{64}}+{\frac {35}{256}}+{\frac {315}{4096}}+{\frac {693}{16384}}+\cdots.$

It is not known whether${\sqrt {2}}$can be represented with aBBP-type formula.BBP-type formulas are known forπ√2and√2 ln(1+√2),however.

The number can be represented by an infinite series ofEgyptian fractions,with denominators defined by 2ⁿ th terms of aFibonacci-likerecurrence relationa(n) = 34a(n−1) −a(n−2),a(0) = 0,a(1) = 6.

${\sqrt {2}}={\frac {3}{2}}-{\frac {1}{2}}\sum _{n=0}^{\infty }{\frac {1}{a(2^{n})}}={\frac {3}{2}}-{\frac {1}{2}}\left({\frac {1}{6}}+{\frac {1}{204}}+{\frac {1}{235416}}+\dots \right)$

Continued fraction

The square root of 2 and approximations byconvergents of continued fractions

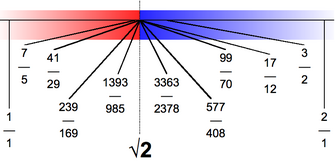
The square root of two has the followingcontinued fractionrepresentation:

${\sqrt {2}}=1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ddots }}}}}}.$

Theconvergents⁠p/q⁠formed by truncating this representation form a sequence of fractions that approximate the square root of two to increasing accuracy, and that are described by thePell numbers(i.e.,p²− 2q²= ±1). The first convergents are:⁠1/1⁠,⁠3/2⁠,⁠7/5⁠,⁠17/12⁠,⁠41/29⁠,⁠99/70⁠,⁠239/169⁠,⁠577/408⁠and the convergent following⁠p/q⁠is⁠p+ 2q/p+q⁠.The convergent⁠p/q⁠differs from${\sqrt {2}}$by almost exactly⁠1/2√2q²⁠,which follows from:

$\left|{\sqrt {2}}-{\frac {p}{q}}\right|={\frac {|2q^{2}-p^{2}|}{q^{2}\!\left({\sqrt {2}}+{\frac {p}{q}}\right)}}={\frac {1}{q^{2}\!\left({\sqrt {2}}+{\frac {p}{q}}\right)}}\thickapprox {\frac {1}{2{\sqrt {2}}q^{2}}}$

Nested square

The following nested square expressions converge to${\textstyle {\sqrt {2}}}$:

${\begin{aligned}{\sqrt {2}}&={\tfrac {3}{2}}-2\left({\tfrac {1}{4}}-\left({\tfrac {1}{4}}-{\bigl (}{\tfrac {1}{4}}-\cdots {\bigr )}^{2}\right)^{2}\right)^{2}\\[10mu]&={\tfrac {3}{2}}-4\left({\tfrac {1}{8}}+\left({\tfrac {1}{8}}+{\bigl (}{\tfrac {1}{8}}+\cdots {\bigr )}^{2}\right)^{2}\right)^{2}.\end{aligned}}$

Applications

Paper size

The A series of paper sizes

In 1786, German physics professorGeorg Christoph Lichtenbergfound that any sheet of paper whose long edge is${\sqrt {2}}$times longer than its short edge could be folded in half and aligned with its shorter side to produce a sheet with exactly the same proportions as the original. This ratio of lengths of the longer over the shorter side guarantees that cutting a sheet in half along a line results in the smaller sheets having the same (approximate) ratio as the original sheet. When Germany standardisedpaper sizesat the beginning of the 20th century, they used Lichtenberg's ratio to create the"A" seriesof paper sizes.Today, the (approximate)aspect ratioof paper sizes underISO 216(A4, A0, etc.) is 1:${\sqrt {2}}$.

Proof:
Let$S=$shorter length and$L=$longer length of the sides of a sheet of paper, with

$R={\frac {L}{S}}={\sqrt {2}}$as required by ISO 216.

Let$R'={\frac {L'}{S'}}$be the analogous ratio of the halved sheet, then

$R'={\frac {S}{L/2}}={\frac {2S}{L}}={\frac {2}{(L/S)}}={\frac {2}{\sqrt {2}}}={\sqrt {2}}=R$.

Physical sciences

There are some interesting properties involving the square root of 2 in thephysical sciences:

• The square root of two is thefrequency ratioof atritoneinterval in twelve-toneequal temperamentmusic.
• The square root of two forms the relationship off-stopsin photographic lenses, which in turn means that the ratio ofareasbetween two successiveaperturesis 2.
• The celestial latitude (declination) of the Sun during a planet's astronomicalcross-quarter daypoints equals the tilt of the planet's axis divided by${\sqrt {2}}$.

Distances betweenverticesof a doubleunit cubearesquare rootsof the first sixnatural numbers,including the square root of 2 (√7 is not possible due toLegendre's three-square theorem)

• In the brain there are lattice cells, discovered in 2005 by a group led by May-Britt and Edvard Moser. "The grid cells were found in the cortical area located right next to the hippocampus [...] At one end of this cortical area the mesh size is small and at the other it is very large. However, the increase in mesh size is not left to chance, but increases by the squareroot of two from one area to the next."

See also

• List of mathematical constants
• Square root of 3,√3
• Square root of 5,√5
• Gelfond–Schneider constant,2^√2
• Silver ratio,1 +√2

References

• Apostol, Tom M.(2000), "Irrationality of the square root of two – A geometric proof",American Mathematical Monthly,107(9): 841–842,doi:10.2307/2695741,JSTOR2695741.
• Aristotle(2007),Analytica priora,eBooks@Adelaide
• Bishop, Errett (1985), Schizophrenia in contemporary mathematics. Errett Bishop: reflections on him and his research (San Diego, Calif., 1983), 1–32, Contemp. Math. 39, Amer. Math. Soc., Providence, RI.
• Flannery, David (2005),The Square Root of Two,Springer-Verlag,ISBN0-387-20220-X.
• Fowler, David;Robson, Eleanor(1998), "Square Root Approximations in Old Babylonian Mathematics: YBC 7289 in Context",Historia Mathematica,25(4): 366–378,doi:10.1006/hmat.1998.2209.
• Good, I. J.;Gover, T. N. (1967), "The generalized serial test and the binary expansion of${\sqrt {2}}$",Journal of the Royal Statistical Society, Series A,130(1): 102–107,doi:10.2307/2344040,JSTOR2344040.
• Henderson, David W. (2000), "Square roots in the Śulba Sūtras", in Gorini, Catherine A. (ed.),Geometry At Work: Papers in Applied Geometry,Cambridge University Press, pp. 39–45,ISBN978-0-88385-164-7.

External links

• Gourdon, X.; Sebah, P. (2001), "Pythagoras' Constant:${\sqrt {2}}$",Numbers, Constants and Computation.
• The Square Root of Two to 5 million digitsby Jerry Bonnell andRobert J. Nemiroff.May, 1994.
• Square root of 2 is irrational,a collection of proofs
• Grime, James; Bowley, Roger."The Square Root${\sqrt {2}}$of Two ".Numberphile.Brady Haran.
• √2Search Engine2 billion searchable digits of√2,πande