Topology

For other uses, seeTopology (disambiguation).

Not to be confused withtopographyortypology.

A three-dimensional model of afigure-eight knot.The figure-eight knot is aprime knotand has anAlexander–Briggs notationof 4₁.

Topology(from theGreekwordsτόπος,'place, location', andλόγος,'study') is the part ofmathematicsconcerned with the properties of ageometric objectthat are preserved undercontinuousdeformations,such asstretching,twisting,crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself.

Atopological spaceis asetendowed with a structure, called atopology,which allows defining continuous deformation of subspaces, and, more generally, all kinds ofcontinuity.Euclidean spaces,and, more generally,metric spacesare examples of topological spaces, as any distance or metric defines a topology. The deformations that are considered in topology arehomeomorphismsandhomotopies.A property that is invariant under such deformations is atopological property.The following are basic examples of topological properties: thedimension,which allows distinguishing between alineand asurface;compactness,which allows distinguishing between a line and a circle;connectedness,which allows distinguishing a circle from two non-intersecting circles.

The ideas underlying topology go back toGottfried Wilhelm Leibniz,who in the 17th century envisioned thegeometria situsandanalysis situs.Leonhard Euler'sSeven Bridges of Königsbergproblem andpolyhedron formulaare arguably the field's first theorems. The termtopologywas introduced byJohann Benedict Listingin the 19th century; although, it was not until the first decades of the 20th century that the idea of a topological space was developed.

Motivation

Möbius strips,which have only one surface and one edge, are a kind of object studied in topology.

The motivating insight behind topology is that some geometric problems depend not on the exact shape of the objects involved, but rather on the way they are put together. For example, the square and the circle have many properties in common: they are both one dimensional objects (from a topological point of view) and both separate the plane into two parts, the part inside and the part outside.

In one of the first papers in topology,Leonhard Eulerdemonstrated that it was impossible to find a route through the town of Königsberg (nowKaliningrad) that would cross each of its seven bridges exactly once. This result did not depend on the lengths of the bridges or on their distance from one another, but only on connectivity properties: which bridges connect to which islands or riverbanks. ThisSeven Bridges of Königsbergproblem led to the branch of mathematics known asgraph theory.

Similarly, thehairy ball theoremof algebraic topology says that "one cannot comb the hair flat on a hairy ball without creating acowlick."This fact is immediately convincing to most people, even though they might not recognize the more formal statement of the theorem, that there is no nonvanishing continuoustangent vector fieldon the sphere. As with theBridges of Königsberg,the result does not depend on the shape of the sphere; it applies to any kind of smooth blob, as long as it has no holes.

To deal with these problems that do not rely on the exact shape of the objects, one must be clear about just what properties these problems do rely on. From this need arises the notion ofhomeomorphism.The impossibility of crossing each bridge just once applies to any arrangement of bridgeshomeomorphicto those in Königsberg, and the hairy ball theorem applies to any space homeomorphic to a sphere.

Intuitively, two spaces are homeomorphic if one can be deformed into the other without cutting or gluing. A traditional joke is that a topologist cannot distinguish a coffee mug from a doughnut, since a sufficiently pliable doughnut could be reshaped to a coffee cup by creating a dimple and progressively enlarging it, while shrinking the hole into a handle.

Homeomorphism can be considered the most basictopological equivalence.Another ishomotopy equivalence.This is harder to describe without getting technical, but the essential notion is that two objects are homotopy equivalent if they both result from "squishing" some larger object.

History

TheSeven Bridges of Königsbergwas a problem solved by Euler.

See also:History of the separation axioms

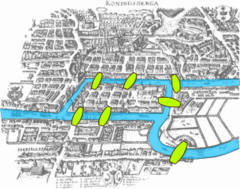
Topology, as a well-defined mathematical discipline, originates in the early part of the twentieth century, but some isolated results can be traced back several centuries.Among these are certain questions in geometry investigated byLeonhard Euler.His 1736 paper on theSeven Bridges of Königsbergis regarded as one of the first practical applications of topology.On 14 November 1750, Euler wrote to a friend that he had realized the importance of theedgesof apolyhedron.This led to hispolyhedron formula,V−E+F= 2(whereV,E,andFrespectively indicate the number of vertices, edges, and faces of the polyhedron). Some authorities regard this analysis as the first theorem, signaling the birth of topology.

Further contributions were made byAugustin-Louis Cauchy,Ludwig Schläfli,Johann Benedict Listing,Bernhard RiemannandEnrico Betti.Listing introduced the term "Topologie" inVorstudien zur Topologie,written in his native German, in 1847, having used the word for ten years in correspondence before its first appearance in print.The English form "topology" was used in 1883 in Listing's obituary in the journalNatureto distinguish "qualitative geometry from the ordinary geometry in which quantitative relations chiefly are treated".

Their work was corrected, consolidated and greatly extended byHenri Poincaré.In 1895, he published his ground-breaking paper onAnalysis Situs,which introduced the concepts now known ashomotopyandhomology,which are now considered part ofalgebraic topology.

Topological characteristics of closed 2-manifolds

Manifold	Euler num	Orientability	Betti numbers			Torsion coefficient(1-dim)
			b0	b1	b2
Sphere	2	Orientable	1	0	1	none
Torus	0	Orientable	1	2	1	none
2-holed torus	−2	Orientable	1	4	1	none
g-holed torus (genusg)	2 − 2g	Orientable	1	2g	1	none
Projective plane	1	Non-orientable	1	0	0	2
Klein bottle	0	Non-orientable	1	1	0	2
Sphere withccross-caps(c> 0)	2 −c	Non-orientable	1	c− 1	0	2
2-Manifold withgholes andccross-caps (c> 0)	2 − (2g+c)	Non-orientable	1	(2g+c) − 1	0	2

Unifying the work on function spaces ofGeorg Cantor,Vito Volterra,Cesare Arzelà,Jacques Hadamard,Giulio Ascoliand others,Maurice Fréchetintroduced themetric spacein 1906.A metric space is now considered a special case of a general topological space, with any given topological space potentially giving rise to many distinct metric spaces. In 1914,Felix Hausdorffcoined the term "topological space" and gave the definition for what is now called aHausdorff space.Currently, a topological space is a slight generalization of Hausdorff spaces, given in 1922 byKazimierz Kuratowski.

Modern topology depends strongly on the ideas of set theory, developed by Georg Cantor in the later part of the 19th century. In addition to establishing the basic ideas of set theory, Cantor considered point sets inEuclidean spaceas part of his study ofFourier series.For further developments, seepoint-set topologyand algebraic topology.

The 2022Abel Prizewas awarded toDennis Sullivan"for his groundbreaking contributions to topology in its broadest sense, and in particular its algebraic, geometric and dynamical aspects".

Concepts

Topologies on sets

Main article:Topological space

The termtopologyalso refers to a specific mathematical idea central to the area of mathematics called topology. Informally, a topology describes how elements of a set relate spatially to each other. The same set can have different topologies. For instance, thereal line,thecomplex plane,and theCantor setcan be thought of as the same set with different topologies.

Formally, letXbe a set and letτbe afamilyof subsets ofX.Thenτis called a topology onXif:

1. Both the empty set andXare elements ofτ.
2. Any union of elements ofτis an element ofτ.
3. Any intersection of finitely many elements ofτis an element ofτ.

Ifτis a topology onX,then the pair(X,τ)is called a topological space. The notationX_τmay be used to denote a setXendowed with the particular topologyτ.By definition, every topology is aπ-system.

The members ofτare calledopen setsinX.A subset ofXis said to be closed if its complement is inτ(that is, its complement is open). A subset ofXmay be open, closed, both (aclopen set), or neither. The empty set andXitself are always both closed and open. An open subset ofXwhich contains a pointxis called aneighborhoodofx.

Continuous functions and homeomorphisms

A continuous deformation (a type of homeomorphism) of a mug into a doughnut (torus) and of a (holeless) cow into a sphere

A continuous transformation can turn a coffee mug into a donut.
Ceramic model by Keenan Crane andHenry Segerman.

Main articles:Continuous functionandhomeomorphism

Afunctionor map from one topological space to another is calledcontinuousif the inverseimageof any open set is open. If the function maps thereal numbersto the real numbers (both spaces with the standard topology), then this definition of continuous is equivalent to the definition of continuous incalculus.If a continuous function isone-to-oneandonto,and if the inverse of the function is also continuous, then the function is called a homeomorphism and the domain of the function is said to be homeomorphic to the range. Another way of saying this is that the function has a natural extension to the topology. If two spaces are homeomorphic, they have identical topological properties, and are considered topologically the same. The cube and the sphere are homeomorphic, as are the coffee cup and the doughnut. However, the sphere is not homeomorphic to the doughnut.

Manifolds

Main article:Manifold

While topological spaces can be extremely varied and exotic, many areas of topology focus on the more familiar class of spaces known as manifolds. Amanifoldis a topological space that resembles Euclidean space near each point. More precisely, each point of ann-dimensional manifold has aneighborhoodthat ishomeomorphicto the Euclidean space of dimensionn.Linesandcircles,but notfigure eights,are one-dimensional manifolds. Two-dimensional manifolds are also calledsurfaces,although not allsurfacesare manifolds. Examples include theplane,the sphere, and the torus, which can all be realized without self-intersection in three dimensions, and theKlein bottleandreal projective plane,which cannot (that is, all their realizations are surfaces that are not manifolds).

Topics

General topology

Main article:General topology

General topology is the branch of topology dealing with the basic set-theoretic definitions and constructions used in topology.It is the foundation of most other branches of topology, including differential topology, geometric topology, and algebraic topology. Another name for general topology is point-set topology.

The basic object of study istopological spaces,which are sets equipped with atopology,that is, a family ofsubsets,calledopen sets,which isclosedunder finiteintersectionsand (finite or infinite)unions.The fundamental concepts of topology, such ascontinuity,compactness,andconnectedness,can be defined in terms of open sets. Intuitively, continuous functions take nearby points to nearby points. Compact sets are those that can be covered by finitely many sets of arbitrarily small size. Connected sets are sets that cannot be divided into two pieces that are far apart. The wordsnearby,arbitrarily small,andfar apartcan all be made precise by using open sets. Several topologies can be defined on a given space. Changing a topology consists of changing the collection of open sets. This changes which functions are continuous and which subsets are compact or connected.

Metric spacesare an important class of topological spaces where the distance between any two points is defined by a function called ametric.In a metric space, an open set is a union of open disks, where an open disk of radiusrcentered atxis the set of all points whose distance toxis less thanr.Many common spaces are topological spaces whose topology can be defined by a metric. This is the case of thereal line,thecomplex plane,real and complexvector spacesandEuclidean spaces.Having a metric simplifies many proofs.

Algebraic topology

Main article:Algebraic topology

Algebraic topology is a branch of mathematics that uses tools fromalgebrato study topological spaces.The basic goal is to find algebraic invariants thatclassifytopological spacesup tohomeomorphism, though usually most classify up to homotopy equivalence.

The most important of these invariants arehomotopy groups,homology, andcohomology.

Although algebraic topology primarily uses algebra to study topological problems, using topology to solve algebraic problems is sometimes also possible. Algebraic topology, for example, allows for a convenient proof that any subgroup of afree groupis again a free group.

Differential topology

Main article:Differential topology

Differential topology is the field dealing withdifferentiable functionsondifferentiable manifolds.It is closely related todifferential geometryand together they make up the geometric theory of differentiable manifolds.

More specifically, differential topology considers the properties and structures that require only asmooth structureon a manifold to be defined. Smooth manifolds are "softer" than manifolds with extra geometric structures, which can act as obstructions to certain types of equivalences anddeformationsthat exist in differential topology. For instance, volume andRiemannian curvatureare invariants that can distinguish different geometric structures on the same smooth manifold – that is, one can smoothly "flatten out" certain manifolds, but it might require distorting the space and affecting the curvature or volume.

Geometric topology

Main article:Geometric topology

Geometric topology is a branch of topology that primarily focuses on low-dimensionalmanifolds(that is, spaces of dimensions 2, 3, and 4) and their interaction with geometry, but it also includes some higher-dimensional topology.Some examples of topics in geometric topology areorientability,handle decompositions,local flatness,crumpling and the planar and higher-dimensionalSchönflies theorem.

In high-dimensional topology,characteristic classesare a basic invariant, andsurgery theoryis a key theory.

Low-dimensional topology is strongly geometric, as reflected in theuniformization theoremin 2 dimensions – every surface admits a constant curvature metric; geometrically, it has one of 3 possible geometries: positivecurvature/spherical, zero curvature/flat, and negative curvature/hyperbolic – and thegeometrization conjecture(now theorem) in 3 dimensions – every 3-manifold can be cut into pieces, each of which has one of eight possible geometries.

2-dimensional topology can be studied ascomplex geometryin one variable (Riemannsurfaces are complex curves) – by the uniformization theorem everyconformal classofmetricsis equivalent to a unique complex one, and 4-dimensional topology can be studied from the point of view of complex geometry in two variables (complex surfaces), though not every 4-manifold admits a complex structure.

Generalizations

Occasionally, one needs to use the tools of topology but a "set of points" is not available. Inpointless topologyone considers instead thelatticeof open sets as the basic notion of the theory,whileGrothendieck topologiesare structures defined on arbitrarycategoriesthat allow the definition ofsheaveson those categories, and with that the definition of general cohomology theories.

Applications

Biology

Topology has been used to study various biological systems including molecules and nanostructure (e.g., membraneous objects). In particular,circuit topologyandknot theoryhave been extensively applied to classify and compare the topology of folded proteins and nucleic acids.Circuit topologyclassifies folded molecular chains based on the pairwise arrangement of their intra-chain contacts and chain crossings.Knot theory,a branch of topology, is used in biology to study the effects of certain enzymes on DNA. These enzymes cut, twist, and reconnect the DNA, causing knotting with observable effects such as slowerelectrophoresis.

Computer science

Topological data analysisuses techniques from algebraic topology to determine the large scale structure of a set (for instance, determining if a cloud of points is spherical ortoroidal). The main method used by topological data analysis is to:

1. Replace a set of data points with a family ofsimplicial complexes,indexed by a proximity parameter.
2. Analyse these topological complexes via algebraic topology – specifically, via the theory ofpersistent homology.
3. Encode the persistent homology of a data set in the form of a parameterized version of aBetti number,which is called a barcode.

Several branches ofprogramming language semantics,such asdomain theory,are formalized using topology. In this context,Steve Vickers,building on work bySamson AbramskyandMichael B. Smyth,characterizes topological spaces asBooleanorHeyting algebrasover open sets, which are characterized assemidecidable(equivalently, finitely observable) properties.

Physics

Topology is relevant to physics in areas such ascondensed matter physics,quantum field theoryandphysical cosmology.

The topological dependence of mechanical properties in solids is of interest in disciplines ofmechanical engineeringandmaterials science.Electrical and mechanical properties depend on the arrangement and network structures ofmoleculesand elementary units in materials.Thecompressive strengthofcrumpledtopologies is studied in attempts to understand the high strength to weight of such structures that are mostly empty space.Topology is of further significance inContact mechanicswhere the dependence of stiffness and friction on thedimensionalityof surface structures is the subject of interest with applications in multi-body physics.

Atopological quantum field theory(or topological field theory or TQFT) is a quantum field theory that computestopological invariants.

Although TQFTs were invented by physicists, they are also of mathematical interest, being related to, among other things,knot theory,the theory offour-manifoldsin algebraic topology, and to the theory ofmoduli spacesin algebraic geometry.Donaldson,Jones,Witten,andKontsevichhave all wonFields Medalsfor work related to topological field theory.

The topological classification ofCalabi–Yau manifoldshas important implications instring theory,as different manifolds can sustain different kinds of strings.

In cosmology, topology can be used to describe the overallshape of the universe.This area of research is commonly known asspacetime topology.

In condensed matter a relevant application to topological physics comes from the possibility to obtain one-way current, which is a current protected from backscattering. It was first discovered in electronics with the famousquantum Hall effect,and then generalized in other areas of physics, for instance in photonicsbyF.D.M Haldane.

Robotics

The possible positions of arobotcan be described by amanifoldcalledconfiguration space.In the area ofmotion planning,one finds paths between two points in configuration space. These paths represent a motion of the robot'sjointsand other parts into the desired pose.

Games and puzzles

Disentanglement puzzlesare based on topological aspects of the puzzle's shapes and components.

Fiber art

In order to create a continuous join of pieces in a modular construction, it is necessary to create an unbroken path in an order which surrounds each piece and traverses each edge only once. This process is an application of theEulerian path.

Resources and research

Major journals

• Geometry & Topology-amathematic research journalfocused on geometry and topology, and their applications, published byMathematical Sciences Publishers.
• Journal of Topology-ascientific journalwhich publishes papers of high quality and significance in topology,geometry,and adjacent areas of mathematics.

Major books

• Munkres, James R. (2000).Topology(2nd ed.). Upper Saddle River, NJ: Prentice Hall.ISBN978-0-13-181629-9
• Willard, Stephen (2016).General topology.Dover books on mathematics. Mineola, N.Y: Dover publications.ISBN978-0-486-43479-7
• Armstrong, M. A. (1983).Basic topology.Undergraduate texts in mathematics. New York: Springer-Verlag.ISBN978-0-387-90839-7

See also

• Characterizations of the category of topological spaces
• Equivariant topology
• List of algebraic topology topics
• List of examples in general topology
• List of general topology topics
• List of geometric topology topics
• List of topology topics
• Publications in topology
• Topoisomer
• Topology glossary
• Topological Galois theory
• Topological geometry
• Topological order

References

Bibliography

• Aleksandrov, P.S. (1969) [1956]. "Chapter XVIII Topology". In Aleksandrov, A.D.; Kolmogorov, A.N.; Lavrent'ev, M.A. (eds.).Mathematics / Its Content, Methods and Meaning(2nd ed.). The M.I.T. Press.
• Croom, Fred H. (1989).Principles of Topology.Saunders College Publishing.ISBN978-0-03-029804-2.
• Richeson, D.(2008).Euler's Gem: The Polyhedron Formula and the Birth of Topology.Princeton University Press.

Further reading

• Ryszard Engelking,General Topology,Heldermann Verlag, Sigma Series in Pure Mathematics, December 1989,ISBN3-88538-006-4.
• Bourbaki;Elements of Mathematics: General Topology,Addison–Wesley (1966).
• Breitenberger, E. (2006). "Johann Benedict Listing". In James, I.M. (ed.).History of Topology.North Holland.ISBN978-0-444-82375-5.
• Kelley, John L.(1975).General Topology.Springer-Verlag.ISBN978-0-387-90125-1.
• Brown, Ronald(2006).Topology and Groupoids.Booksurge.ISBN978-1-4196-2722-4.(Provides a well motivated, geometric account of general topology, and shows the use of groupoids in discussingvan Kampen's theorem,covering spaces,andorbit spaces.)
• Wacław Sierpiński,General Topology,Dover Publications, 2000,ISBN0-486-41148-6
• Pickover, Clifford A.(2006).The Möbius Strip: Dr. August Möbius's Marvelous Band in Mathematics, Games, Literature, Art, Technology, and Cosmology.Thunder's Mouth Press.ISBN978-1-56025-826-1.(Provides a popular introduction to topology and geometry)
• Gemignani, Michael C. (1990) [1967].Elementary Topology(2nd ed.). Dover Publications Inc.ISBN978-0-486-66522-1.

External links

• "Topology, general".Encyclopedia of Mathematics.EMS Press.2001 [1994].
• Elementary Topology: A First CourseViro, Ivanov, Netsvetaev, Kharlamov.
• TopologyatCurlie
• The Topological ZooatThe Geometry Center.
• Topology Atlas
• Topology Course Lecture NotesAisling McCluskey and Brian McMaster, Topology Atlas.
• Topology Glossary
• Moscow 1935: Topology moving towards America,a historical essay byHassler Whitney.