Unification (computer science)

Inlogicandcomputer science,specificallyautomated reasoning,unificationis an algorithmic process ofsolving equationsbetween symbolicexpressions,each of the formLeft-hand side = Right-hand side.For example, usingx,y,zas variables, and takingfto be anuninterpreted function,thesingletonequation set {f(1,y) =f(x,2) } is a syntactic first-order unification problem that has the substitution {x↦1,y↦ 2 } as its only solution.

Conventions differ on what values variables may assume and which expressions are considered equivalent. In first-order syntactic unification, variables range overfirst-order termsand equivalence is syntactic. This version of unification has a unique "best" answer and is used inlogic programmingand programming languagetype systemimplementation, especially inHindley–Milnerbasedtype inferencealgorithms. In higher-order unification, possibly restricted tohigher-order pattern unification,terms may include lambda expressions, and equivalence is up to beta-reduction. This version is used in proof assistants and higher-order logic programming, for exampleIsabelle,Twelf,andlambdaProlog.Finally, in semantic unification or E-unification, equality is subject to background knowledge and variables range over a variety of domains. This version is used inSMT solvers,term rewritingalgorithms, andcryptographic protocolanalysis.

Formal definition

Aunification problemis a finite setE={l₁≐r₁,...,l_n≐r_n}of equations to solve, wherel_i,r_iare in the set$T$oftermsorexpressions.Depending on which expressions or terms are allowed to occur in an equation set or unification problem, and which expressions are considered equal, several frameworks of unification are distinguished. If higher-order variables, that is, variables representingfunctions,are allowed in an expression, the process is calledhigher-order unification,otherwisefirst-order unification.If a solution is required to make both sides of each equation literally equal, the process is calledsyntacticorfreeunification,otherwisesemanticorequational unification,orE-unification,orunification modulo theory.

If the right side of each equation is closed (no free variables), the problem is called (pattern)matching.The left side (with variables) of each equation is called thepattern.

Prerequisites

Formally, a unification approach presupposes

• An infinite set$V$ofvariables.For higher-order unification, it is convenient to choose$V$disjoint from the set oflambda-term bound variables.
• A set$T$oftermssuch that$V\subseteq T$.For first-order unification,$T$is usually the set offirst-order terms(terms built from variable and function symbols). For higher-order unification$T$consists of first-order terms andlambda terms(terms containing some higher-order variables).
• A mapping${\text{vars}}\colon T\rightarrow$$\mathbb {P}$$(V)$,assigning to each term$t$the set${\text{vars}}(t)\subsetneq V$offree variablesoccurring in$t$.
• A theory orequivalence relation$\equiv$on$T$,indicating which terms are considered equal. For first-order E-unification,$\equiv$reflects the background knowledge about certain function symbols; for example, if$\oplus$is considered commutative,$t\equiv u$if$u$results from$t$by swapping the arguments of$\oplus$at some (possibly all) occurrences.In the most typical case that there is no background knowledge at all, then only literally, or syntactically, identical terms are considered equal. In this case, ≡ is called thefree theory(because it is afree object), theempty theory(because the set of equationalsentences,or the background knowledge, is empty), thetheory ofuninterpreted functions(because unification is done on uninterpretedterms), or thetheory ofconstructors(because all function symbols just build up data terms, rather than operating on them). For higher-order unification, usually$t\equiv u$if$t$and$u$areAlpha equivalent.

As an example of how the set of terms and theory affects the set of solutions, the syntactic first-order unification problem {y=cons(2,y) } has no solution over the set offinite terms.However, it has the single solution {y↦cons(2,cons(2,cons(2,...))) } over the set ofinfinite treeterms. Similarly, the semantic first-order unification problem {a⋅x=x⋅a} has each substitution of the form {x↦a⋅...⋅a} as a solution in asemigroup,i.e. if (⋅) is consideredassociative.But the same problem, viewed in anabelian group,where (⋅) is considered alsocommutative,has any substitution at all as a solution.

As an example of higher-order unification, the singleton set {a=y(x) } is a syntactic second-order unification problem, sinceyis a function variable. One solution is {x↦a,y↦ (identity function) }; another one is {y↦ (constant functionmapping each value toa),x↦(any value)}.

Substitution

Main article:Substitution (logic)

Asubstitutionis a mapping$\sigma:V\rightarrow T$from variables to terms; the notation$\{x_{1}\mapsto t_{1},...,x_{k}\mapsto t_{k}\}$refers to a substitution mapping each variable$x_{i}$to the term$t_{i}$,for$i=1,...,k$,and every other variable to itself; the$x_{i}$must be pairwise distinct.Applyingthat substitution to a term$t$is written inpostfix notationas$t\{x_{1}\mapsto t_{1},...,x_{k}\mapsto t_{k}\}$;it means to (simultaneously) replace every occurrence of each variable$x_{i}$in the term$t$by$t_{i}$.The result$t\tau$of applying a substitution$\tau$to a term$t$is called aninstanceof that term$t$. As a first-order example, applying the substitution{x↦h(a,y),z↦b}to the term

	$f($	${\textbf {x}}$	${\displaystyle,a,g(}$	${\textbf {z}}$	$),y)$
yields
	$f($	${\textbf {h}}({\textbf {a}},{\textbf {y}})$	${\displaystyle,a,g(}$	${\textbf {b}}$	$),y).$

Generalization, specialization

If a term$t$has an instance equivalent to a term$u$,that is, if$t\sigma \equiv u$for some substitution$\sigma$,then$t$is calledmore generalthan$u$,and$u$is calledmore specialthan, orsubsumedby,$t$.For example,$x\oplus a$is more general than$a\oplus b$if ⊕ iscommutative,since then$(x\oplus a)\{x\mapsto b\}=b\oplus a\equiv a\oplus b$.

If ≡ is literal (syntactic) identity of terms, a term may be both more general and more special than another one only if both terms differ just in their variable names, not in their syntactic structure; such terms are calledvariants,orrenamingsof each other. For example, $f(x_{1},a,g(z_{1}),y_{1})$ is a variant of $f(x_{2},a,g(z_{2}),y_{2})$, since $$f(x_{1},a,g(z_{1}),y_{1})\{x_{1}\mapsto x_{2},y_{1}\mapsto y_{2},z_{1}\mapsto z_{2}\}=f(x_{2},a,g(z_{2}),y_{2})$$ and $$f(x_{2},a,g(z_{2}),y_{2})\{x_{2}\mapsto x_{1},y_{2}\mapsto y_{1},z_{2}\mapsto z_{1}\}=f(x_{1},a,g(z_{1}),y_{1}).$$ However,$f(x_{1},a,g(z_{1}),y_{1})$isnota variant of$f(x_{2},a,g(x_{2}),x_{2})$,since no substitution can transform the latter term into the former one. The latter term is therefore properly more special than the former one.

For arbitrary$\equiv$,a term may be both more general and more special than a structurally different term. For example, if ⊕ isidempotent,that is, if always$x\oplus x\equiv x$,then the term$x\oplus y$is more general than$z$,and vice versa,although$x\oplus y$and$z$are of different structure.

A substitution$\sigma$ismore specialthan, orsubsumedby, a substitution$\tau$if$t\sigma$is subsumed by$t\tau$for each term$t$.We also say that$\tau$is more general than$\sigma$.More formally, take a nonempty infinite set$V$of auxiliary variables such that no equation$l_{i}\doteq r_{i}$in the unification problem contains variables from$V$.Then a substitution$\sigma$is subsumed by another substitution$\tau$if there is a substitution$\theta$such that for all terms$X\notin V$,$X\sigma \equiv X\tau \theta$. For instance$\{x\mapsto a,y\mapsto a\}$is subsumed by$\tau =\{x\mapsto y\}$,using$\theta =\{y\mapsto a\}$,but $\sigma =\{x\mapsto a\}$is not subsumed by$\tau =\{x\mapsto y\}$,as$f(x,y)\sigma =f(a,y)$is not an instance of $f(x,y)\tau =f(y,y)$.

Solution set

A substitution σ is asolutionof the unification problemEifl_iσ ≡r_iσfor$i=1,...,n$.Such a substitution is also called aunifierofE. For example, if ⊕ isassociative,the unification problem {x⊕a≐a⊕x} has the solutions {x↦a}, {x↦a⊕a}, {x↦a⊕a⊕a}, etc., while the problem {x⊕a≐a} has no solution.

For a given unification problemE,a setSof unifiers is calledcompleteif each solution substitution is subsumed by some substitution inS.A complete substitution set always exists (e.g. the set of all solutions), but in some frameworks (such as unrestricted higher-order unification) the problem of determining whether any solution exists (i.e., whether the complete substitution set is nonempty) is undecidable.

The setSis calledminimalif none of its members subsumes another one. Depending on the framework, a complete and minimal substitution set may have zero, one, finitely many, or infinitely many members, or may not exist at all due to an infinite chain of redundant members.Thus, in general, unification algorithms compute a finite approximation of the complete set, which may or may not be minimal, although most algorithms avoid redundant unifiers when possible.For first-order syntactical unification, Martelli and Montanarigave an algorithm that reports unsolvability or computes a single unifier that by itself forms a complete and minimal substitution set, called themost general unifier.

Syntactic unification of first-order terms

Schematic triangle diagram of syntactically unifying termst₁andt₂by a substitution σ

Syntactic unification of first-order termsis the most widely used unification framework. It is based onTbeing the set offirst-order terms(over some given setVof variables,Cof constants andF_nofn-ary function symbols) and on ≡ beingsyntactic equality. In this framework, each solvable unification problem{l₁≐r₁,...,l_n≐r_n}has a complete, and obviously minimal,singletonsolution set{σ}. Its memberσis called themost general unifier(mgu) of the problem. The terms on the left and the right hand side of each potential equation become syntactically equal when the mgu is applied i.e.l₁σ=r₁σ∧... ∧l_nσ=r_nσ. Any unifier of the problem is subsumedby the mguσ. The mgu is unique up to variants: ifS₁andS₂are both complete and minimal solution sets of the same syntactical unification problem, thenS₁= {σ₁} andS₂= {σ₂} for some substitutionsσ₁andσ₂,andxσ₁is a variant ofxσ₂for each variablexoccurring in the problem.

For example, the unification problem {x≐z,y≐f(x) } has a unifier {x↦z,y↦f(z) }, because

x	{x↦z,y↦f(z) }	=	z	=	z	{x↦z,y↦f(z) }	,and
y	{x↦z,y↦f(z) }	=	f(z)	=	f(x)	{x↦z,y↦f(z) }	.

This is also the most general unifier. Other unifiers for the same problem are e.g. {x↦f(x₁),y↦f(f(x₁)),z↦f(x₁) }, {x↦f(f(x₁)),y↦f(f(f(x₁))),z↦f(f(x₁)) }, and so on; there are infinitely many similar unifiers.

As another example, the problemg(x,x) ≐f(y) has no solution with respect to ≡ being literal identity, since any substitution applied to the left and right hand side will keep the outermostgandf,respectively, and terms with different outermost function symbols are syntactically different.

Unification algorithms

Robinson's 1965 unification algorithm

Symbols are ordered such that variables precede function symbols. Terms are ordered by increasing written length; equally long terms are orderedlexicographically.For a setTof terms, its disagreement pathpis the lexicographically least path where two member terms ofTdiffer. Its disagreement set is the set ofsubtermsstarting atp, formally:{t|_p:$t\in T$}.

Algorithm:
Given a setTof terms to be unified
Let$\sigma$initially be theidentity substitution
do forever
if$T\sigma$is asingleton setthen
return$\sigma$
fi
letDbe the disagreement set of$T\sigma$
lets,tbe the two lexicographically least terms inD
ifsis not a variableorsoccurs intthen
return"NONUNIFIABLE"
fi
$\sigma:=\sigma \{s\mapsto t\}$
done

Jacques Herbranddiscussed the basic concepts of unification and sketched an algorithm in 1930.But most authors attribute the first unification algorithm toJohn Alan Robinson(cf. box).Robinson's algorithm had worst-case exponential behavior in both time and space.Numerous authors have proposed more efficient unification algorithms.Algorithms with worst-case linear-time behavior were discovered independently byMartelli & Montanari (1976)andPaterson & Wegman (1976)Baader & Snyder (2001)uses a similar technique as Paterson-Wegman, hence is linear,but like most linear-time unification algorithms is slower than the Robinson version on small sized inputs due to the overhead of preprocessing the inputs and postprocessing of the output, such as construction of aDAGrepresentation.de Champeaux (2022)is also of linear complexity in the input size but is competitive with the Robinson algorithm on small size inputs. The speedup is obtained by using anobject-orientedrepresentation of the predicate calculus that avoids the need for pre- and post-processing, instead making variable objects responsible for creating a substitution and for dealing with aliasing. de Champeaux claims that the ability to add functionality to predicate calculus represented as programmaticobjectsprovides opportunities for optimizing other logic operations as well.

The following algorithm is commonly presented and originates fromMartelli & Montanari (1982).Given a finite set$G=\{s_{1}\doteq t_{1},...,s_{n}\doteq t_{n}\}$of potential equations, the algorithm applies rules to transform it to an equivalent set of equations of the form {x₁≐u₁,...,x_m≐u_m} wherex₁,...,x_mare distinct variables andu₁,...,u_mare terms containing none of thex_i. A set of this form can be read as a substitution. If there is no solution the algorithm terminates with ⊥; other authors use "Ω", or "fail"in that case. The operation of substituting all occurrences of variablexin problemGwith termtis denotedG{x↦t}. For simplicity, constant symbols are regarded as function symbols having zero arguments.

$G\cup \{t\doteq t\}$	$\Rightarrow$	$G$		delete
$G\cup \{f(s_{0},...,s_{k})\doteq f(t_{0},...,t_{k})\}$	$\Rightarrow$	$G\cup \{s_{0}\doteq t_{0},...,s_{k}\doteq t_{k}\}$		decompose
$G\cup \{f(s_{0},\ldots,s_{k})\doteq g(t_{0},...,t_{m})\}$	$\Rightarrow$	$\bot$	if$f\neq g$or$k\neq m$	conflict
$G\cup \{f(s_{0},...,s_{k})\doteq x\}$	$\Rightarrow$	$G\cup \{x\doteq f(s_{0},...,s_{k})\}$		swap
$G\cup \{x\doteq t\}$	$\Rightarrow$	$G\{x\mapsto t\}\cup \{x\doteq t\}$	if$x\not \in {\text{vars}}(t)$and$x\in {\text{vars}}(G)$	eliminate
$G\cup \{x\doteq f(s_{0},...,s_{k})\}$	$\Rightarrow$	$\bot$	if$x\in {\text{vars}}(f(s_{0},...,s_{k}))$	check

Occurs check

Main article:Occurs check

An attempt to unify a variablexwith a term containingxas a strict subtermx≐f(...,x,...) would lead to an infinite term as solution forx,sincexwould occur as a subterm of itself. In the set of (finite) first-order terms as defined above, the equationx≐f(...,x,...) has no solution; hence theeliminaterule may only be applied ifx∉vars(t). Since that additional check, calledoccurs check,slows down the algorithm, it is omitted e.g. in most Prolog systems. From a theoretical point of view, omitting the check amounts to solving equations over infinite trees, see#Unification of infinite termsbelow.

Proof of termination

For the proof of termination of the algorithm consider a triple$\langle n_{var},n_{lhs},n_{eqn}\rangle$ wheren_varis the number of variables that occur more than once in the equation set,n_lhsis the number of function symbols and constants on the left hand sides of potential equations, andn_eqnis the number of equations. When ruleeliminateis applied,n_vardecreases, sincexis eliminated fromGand kept only in {x≐t}. Applying any other rule can never increasen_varagain. When ruledecompose,conflict,orswapis applied,n_lhsdecreases, since at least the left hand side's outermostfdisappears. Applying any of the remaining rulesdeleteorcheckcan't increasen_lhs,but decreasesn_eqn. Hence, any rule application decreases the triple$\langle n_{var},n_{lhs},n_{eqn}\rangle$with respect to thelexicographical order,which is possible only a finite number of times.

Conor McBrideobservesthat "by expressing the structure which unification exploits" in adependently typedlanguage such asEpigram,Robinson's unification algorithmcan be maderecursive on the number of variables,in which case a separate termination proof becomes unnecessary.

Examples of syntactic unification of first-order terms

In the Prolog syntactical convention a symbol starting with an upper case letter is a variable name; a symbol that starts with a lowercase letter is a function symbol; the comma is used as the logicalandoperator. For mathematical notation,x,y,zare used as variables,f,gas function symbols, anda,bas constants.

Prolog notation	Mathematical notation	Unifying substitution	Explanation
a = a	{a=a}	{}	Succeeds. (tautology)
a = b	{a=b}	⊥	aandbdo not match
X = X	{x=x}	{}	Succeeds. (tautology)
a = X	{a=x}	{x↦a}	xis unified with the constanta
X = Y	{x=y}	{x↦y}	xandyare aliased
f(a,X) = f(a,b)	{f(a,x) =f(a,b) }	{x↦b}	function and constant symbols match,xis unified with the constantb
f(a) = g(a)	{f(a) =g(a) }	⊥	fandgdo not match
f(X) = f(Y)	{f(x) =f(y) }	{x↦y}	xandyare aliased
f(X) = g(Y)	{f(x) =g(y) }	⊥	fandgdo not match
f(X) = f(Y,Z)	{f(x) =f(y,z) }	⊥	Fails. Theffunction symbols have different arity
f(g(X)) = f(Y)	{f(g(x)) =f(y) }	{y↦g(x) }	Unifiesywith the term⁠$g(x)$⁠
f(g(X),X) = f(Y,a)	{f(g(x),x) =f(y,a) }	{x↦a,y↦g(a) }	Unifiesxwith constanta,andywith the term⁠$g(a)$⁠
X = f(X)	{x=f(x) }	should be ⊥	Returns ⊥ in first-order logic and many modern Prolog dialects (enforced by theoccurs check). Succeeds in traditional Prolog and in Prolog II, unifyingxwith infinite termx=f(f(f(f(...)))).
X = Y, Y = a	{x=y,y=a}	{x↦a,y↦a}	Bothxandyare unified with the constanta
a = Y, X = Y	{a=y,x=y}	{x↦a,y↦a}	As above (order of equations in set doesn't matter)
X = a, b = X	{x=a,b=x}	⊥	Fails.aandbdo not match, soxcan't be unified with both

Two terms with an exponentially larger tree for their least common instance. Itsdagrepresentation (rightmost, orange part) is still of linear size.

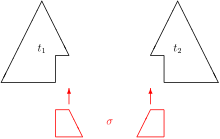
The most general unifier of a syntactic first-order unification problem ofsizenmay have a size of2ⁿ.For example, the problem⁠$(((a*z)*y)*x)*w\doteq w*(x*(y*(z*a)))$⁠has the most general unifier⁠$\{z\mapsto a,y\mapsto a*a,x\mapsto (a*a)*(a*a),w\mapsto ((a*a)*(a*a))*((a*a)*(a*a))\}$⁠,cf. picture. In order to avoid exponential time complexity caused by such blow-up, advanced unification algorithms work ondirected acyclic graphs(dags) rather than trees.

Application: unification in logic programming

The concept of unification is one of the main ideas behindlogic programming.Specifically, unification is a basic building block ofresolution,a rule of inference for determining formula satisfiability. InProlog,the equality symbol=implies first-order syntactic unification. It represents the mechanism of binding the contents of variables and can be viewed as a kind of one-time assignment.

In Prolog:

1. Avariablecan be unified with a constant, a term, or another variable, thus effectively becoming its alias. In many modern Prolog dialects and infirst-order logic,a variable cannot be unified with a term that contains it; this is the so-calledoccurs check.
2. Two constants can be unified only if they are identical.
3. Similarly, a term can be unified with another term if the top function symbols andaritiesof the terms are identical and if the parameters can be unified simultaneously. Note that this is a recursive behavior.
4. Most operations, including+,-,*,/,are not evaluated by=.So for example1+2 = 3is not satisfiable because they are syntactically different. The use of integer arithmetic constraints#=introduces a form of E-unification for which these operations are interpreted and evaluated.

Application: type inference

Type inferencealgorithms are typically based on unification, particularlyHindley-Milnertype inference which is used by the functional languagesHaskellandML.For example, when attempting to infer the type of the Haskell expressionTrue: ['x'],the compiler will use the typea -> [a] -> [a]of the list construction function(:),the typeBoolof the first argumentTrue,and the type[Char]of the second argument['x'].The polymorphic type variableawill be unified withBooland the second argument[a]will be unified with[Char].acannot be bothBoolandCharat the same time, therefore this expression is not correctly typed.

Like for Prolog, an algorithm for type inference can be given:

1. Any type variable unifies with any type expression, and is instantiated to that expression. A specific theory might restrict this rule with an occurs check.
2. Two type constants unify only if they are the same type.
3. Two type constructions unify only if they are applications of the same type constructor and all of their component types recursively unify.

Application: Feature Structure Unification

See also:Feature structure

Unification has been used in different research areas of computational linguistics.

Order-sorted unification

Order-sorted logicallows one to assign asort,ortype,to each term, and to declare a sorts₁asubsortof another sorts₂,commonly written ass₁⊆s₂.For example, when reаsoning about biological creatures, it is useful to declare a sortdogto be a subsort of a sortanimal.Wherever a term of some sortsis required, a term of any subsort ofsmay be supplied instead. For example, assuming a function declarationmother:animal→animal,and a constant declarationlassie:dog,the termmother(lassie) is perfectly valid and has the sortanimal.In order to supply the information that the mother of a dog is a dog in turn, another declarationmother:dog→dogmay be issued; this is calledfunction overloading,similar tooverloading in programming languages.

Walthergave a unification algorithm for terms in order-sorted logic, requiring for any two declared sortss₁,s₂their intersections₁∩s₂to be declared, too: ifx₁andx₂is a variable of sorts₁ands₂,respectively, the equationx₁≐x₂has the solution {x₁=x,x₂=x}, wherex:s₁∩s₂. After incorporating this algorithm into a clause-based automated theorem prover, he could solve a benchmark problem by translating it into order-sorted logic, thereby boiling it down an order of magnitude, as many unary predicates turned into sorts.

Smolka generalized order-sorted logic to allow forparametric polymorphism. In his framework, subsort declarations are propagated to complex type expressions. As a programming example, a parametric sortlist(X) may be declared (withXbeing a type parameter as in aC++ template), and from a subsort declarationint⊆floatthe relationlist(int) ⊆list(float) is automatically inferred, meaning that each list of integers is also a list of floats.

Schmidt-Schauß generalized order-sorted logic to allow for term declarations. As an example, assuming subsort declarationseven⊆intandodd⊆int,a term declaration like ∀i:int.(i+i):evenallows to declare a property of integer addition that could not be expressed by ordinary overloading.

Unification of infinite terms

Background on infinite trees:

• B. Courcelle(1983)."Fundamental Properties of Infinite Trees".Theoret. Comput. Sci.25(2): 95–169.doi:10.1016/0304-3975(83)90059-2.
• Michael J. Maher (Jul 1988). "Complete Axiomatizations of the Algebras of Finite, Rational and Infinite Trees".Proc. IEEE 3rd Annual Symp. on Logic in Computer Science, Edinburgh.pp. 348–357.
• Joxan Jaffar; Peter J. Stuckey (1986)."Semantics of Infinite Tree Logic Programming".Theoretical Computer Science.46:141–158.doi:10.1016/0304-3975(86)90027-7.

Unification algorithm, Prolog II:

• A. Colmerauer(1982). K.L. Clark; S.-A. Tarnlund (eds.).Prolog and Infinite Trees.Academic Press.
• Alain Colmerauer (1984). "Equations and Inequations on Finite and Infinite Trees". In ICOT (ed.).Proc. Int. Conf. on Fifth Generation Computer Systems.pp. 85–99.

Applications:

• Francis Giannesini; Jacques Cohen (1984)."Parser Generation and Grammar Manipulation using Prolog's Infinite Trees".Journal of Logic Programming.1(3): 253–265.doi:10.1016/0743-1066(84)90013-X.

E-unification

E-unificationis the problem of finding solutions to a given set ofequations, taking into account some equational background knowledgeE. The latter is given as a set of universalequalities. For some particular setsE,equation solvingalgorithms(a.k.a.E-unification algorithms) have been devised; for others it has been proven that no such algorithms can exist.

For example, ifaandbare distinct constants, theequation⁠$x*a\doteq y*b$⁠has no solution with respect to purelysyntactic unification, where nothing is known about the operator⁠$*$⁠. However, if the⁠$*$⁠is known to becommutative, then the substitution{x↦b,y↦a}solves the above equation, since

	⁠$x*a$⁠	{x↦b,y↦a}
=	⁠$b*a$⁠		bysubstitution application
=	⁠$a*b$⁠		by commutativity of⁠$*$⁠
=	⁠$y*b$⁠	{x↦b,y↦a}	by (converse) substitution application

The background knowledgeEcould state the commutativity of⁠$*$⁠by the universal equality "⁠$u*v=v*u$⁠for allu,v".

Particular background knowledge sets E

Used naming conventions

∀u,v,w:	⁠$u*(v*w)$⁠	=	⁠$(u*v)*w$⁠	A	Associativity of⁠$*$⁠
∀u,v:	⁠$u*v$⁠	=	⁠$v*u$⁠	C	Commutativity of⁠$*$⁠
∀u,v,w:	⁠$u*(v+w)$⁠	=	⁠$u*v+u*w$⁠	Dl	Left distributivity of⁠$*$⁠over⁠$+$⁠
∀u,v,w:	⁠$(v+w)*u$⁠	=	⁠$v*u+w*u$⁠	Dr	Right distributivity of⁠$*$⁠over⁠$+$⁠
∀u:	⁠$u*u$⁠	=	u	I	Idempotence of⁠$*$⁠
∀u:	⁠$n*u$⁠	=	u	Nl	Left neutral elementnwith respect to⁠$*$⁠
∀u:	⁠$u*n$⁠	=	u	Nr	Right neutral elementnwith respect to⁠$*$⁠

It is said thatunification is decidablefor a theory, if a unification algorithm has been devised for it that terminates foranyinput problem. It is said thatunification issemi-decidablefor a theory, if a unification algorithm has been devised for it that terminates for anysolvableinput problem, but may keep searching forever for solutions of an unsolvable input problem.

Unification is decidablefor the following theories:

• A
• A,C
• A,C,I
• A,C,N_l
• A,I
• A,N_l,N_r(monoid)
• C
• Boolean rings
• Abelian groups,even if the signature is expanded by arbitrary additional symbols (but not axioms)
• K4modal algebras

Unification is semi-decidablefor the following theories:

• A,D_l,D_r
• A,C,D_l
• Commutative rings

One-sided paramodulation

If there is aconvergent term rewriting systemRavailable forE, theone-sided paramodulationalgorithm can be used to enumerate all solutions of given equations.

One-sided paramodulation rules

G∪ {f(s1,...,sn) ≐f(t1,...,tn) }	;S	⇒	G∪ {s1≐t1,...,sn≐tn}	;S		decompose
G∪ {x≐t}	;S	⇒	G{x↦t}	;S{x↦t} ∪ {x↦t}	if the variablexdoesn't occur int	eliminate
G∪ {f(s1,...,sn) ≐t}	;S	⇒	G∪ {s1≐ u1,...,sn≐ un,r≐t}	;S	iff(u1,...,un) →ris a rule fromR	mutate
G∪ {f(s1,...,sn) ≐y}	;S	⇒	G∪ {s1≐y1,...,sn≐yn,y≐f(y1,...,yn) }	;S	ify1,...,ynare new variables	imitate

Starting withGbeing the unification problem to be solved andSbeing the identity substitution, rules are applied nondeterministically until the empty set appears as the actualG,in which case the actualSis a unifying substitution. Depending on the order the paramodulation rules are applied, on the choice of the actual equation fromG,and on the choice ofR's rules inmutate,different computations paths are possible. Only some lead to a solution, while others end at aG≠ {} where no further rule is applicable (e.g.G= {f(...) ≐g(...) }).

Example term rewrite systemR

1	app(nil,z)	→z
2	app(x.y,z)	→x.app(y,z)

For an example, a term rewrite systemRis used defining theappendoperator of lists built fromconsandnil;wherecons(x,y) is written in infix notation asx.yfor brevity; e.g.app(a.b.nil,c.d.nil) →a.app(b.nil,c.d.nil) →a.b.app(nil,c.d.nil) →a.b.c.d.nildemonstrates the concatenation of the listsa.b.nilandc.d.nil,employing the rewrite rule 2,2, and 1. The equational theoryEcorresponding toRis thecongruence closureofR,both viewed as binary relations on terms. For example,app(a.b.nil,c.d.nil) ≡a.b.c.d.nil≡app(a.b.c.d.nil,nil). The paramodulation algorithm enumerates solutions to equations with respect to thatEwhen fed with the exampleR.

A successful example computation path for the unification problem {app(x,app(y,x)) ≐a.a.nil} is shown below. To avoid variable name clashes, rewrite rules are consistently renamed each time before their use by rulemutate;v₂,v₃,... are computer-generated variable names for this purpose. In each line, the chosen equation fromGis highlighted in red. Each time themutaterule is applied, the chosen rewrite rule (1or2) is indicated in parentheses. From the last line, the unifying substitutionS= {y↦nil,x↦a.nil} can be obtained. In fact, app(x,app(y,x)) {y↦nil,x↦a.nil} =app(a.nil,app(nil,a.nil)) ≡app(a.nil,a.nil) ≡a.app(nil,a.nil) ≡a.a.nilsolves the given problem. A second successful computation path, obtainable by choosing "mutate(1), mutate(2), mutate(2), mutate(1)" leads to the substitutionS= {y↦a.a.nil,x↦nil}; it is not shown here. No other path leads to a success.

Example unifier computation

Used rule		G	S
		{app(x,app(y,x)) ≐a.a.nil}	{}
mutate(2)	⇒	{x≐v2.v3,app(y,x) ≐v4,v2.app(v3,v4) ≐a.a.nil}	{}
decompose	⇒	{x≐v2.v3,app(y,x) ≐v4,v2≐a,app(v3,v4) ≐a.nil}	{}
eliminate	⇒	{app(y,v2.v3) ≐v4,v2≐a,app(v3,v4) ≐a.nil}	{x↦v2.v3}
eliminate	⇒	{app(y,a.v3) ≐v4,app(v3,v4) ≐a.nil}	{x↦a.v3}
mutate(1)	⇒	{y≐nil,a.v3≐v5,v5≐v4,app(v3,v4) ≐a.nil}	{x↦a.v3}
eliminate	⇒	{y≐nil,a.v3≐v4,app(v3,v4) ≐a.nil}	{x↦a.v3}
eliminate	⇒	{a.v3≐v4,app(v3,v4) ≐a.nil}	{y↦nil,x↦a.v3}
mutate(1)	⇒	{a.v3≐v4,v3≐nil,v4≐v6,v6≐a.nil}	{y↦nil,x↦a.v3}
eliminate	⇒	{a.v3≐v4,v3≐nil,v4≐a.nil}	{y↦nil,x↦a.v3}
eliminate	⇒	{a.nil≐v4,v4≐a.nil}	{y↦nil,x↦a.nil}
eliminate	⇒	{a.nil≐a.nil}	{y↦nil,x↦a.nil}
decompose	⇒	{a≐a,nil≐nil}	{y↦nil,x↦a.nil}
decompose	⇒	{nil≐nil}	{y↦nil,x↦a.nil}
decompose	⇒	{}	{y↦nil,x↦a.nil}

Narrowing

Triangle diagram of narrowing steps↝tat positionpin terms,with unifying substitution σ (bottom row), using a rewrite rulel→r(top row)

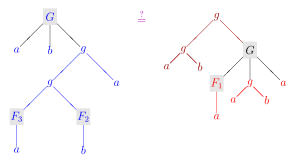
IfRis aconvergent term rewriting systemforE, an approach alternative to the previous section consists in successive application of "narrowingsteps "; this will eventually enumerate all solutions of a given equation. A narrowing step (cf. picture) consists in

• choosing a nonvariable subterm of the current term,
• syntactically unifyingit with the left hand side of a rule fromR,and
• replacing the instantiated rule's right hand side into the instantiated term.

Formally, ifl→ris arenamed copyof a rewrite rule fromR,having no variables in common with a terms,and thesubterms|_pis not a variable and is unifiable withlvia themguσ,thenscan benarrowedto the termt=sσ[rσ]_p,i.e. to the termsσ,with the subterm atpreplacedbyrσ.The situation thatscan be narrowed totis commonly denoted ass↝t. Intuitively, a sequence of narrowing stepst₁↝t₂↝... ↝t_ncan be thought of as a sequence of rewrite stepst₁→t₂→... →t_n,but with the initial termt₁being further and further instantiated, as necessary to make each of the used rules applicable.

Theaboveexample paramodulation computation corresponds to the following narrowing sequence ( "↓" indicating instantiation here):

app(

x

,app(y,

x

))

↓

↓

x↦v2.v3

app(

v2.v3

,app(y,

v2.v3

))

→

v2.app(v3,app(

y

,v2.v3))

↓

y↦nil

v2.app(v3,app(

nil

,v2.v3))

→

v2.app(

v3

,v2.

v3

)

↓

↓

v3↦nil

v2.app(

nil

,v2.

nil

)

→

v2.v2.nil

The last term,v₂.v₂.nilcan be syntactically unified with the original right hand side terma.a.nil.

Thenarrowing lemmaensures that whenever an instance of a termscan be rewritten to a termtby a convergent term rewriting system, thensandtcan be narrowed and rewritten to a terms′andt′,respectively, such thatt′is an instance ofs′.

Formally: wheneversσ→∗tholds for some substitution σ, then there exist termss′,t′such thats↝∗s′andt→∗t′ands′τ=t′for some substitution τ.

Higher-order unification

In Goldfarb'sreduction ofHilbert's 10th problemto second-order unifiability, the equation$X_{1}*X_{2}=X_{3}$corresponds to the depicted unification problem, with function variables$F_{i}$corresponding to$X_{i}$and$G$fresh.

Many applications require one to consider the unification of typed lambda-terms instead of first-order terms. Such unification is often calledhigher-order unification.Higher-order unification isundecidable,and such unification problems do not have most general unifiers. For example, the unification problem {f(a,b,a) ≐d(b,a,c) }, where the only variable isf,has the solutions {f↦ λx.λy.λz.d(y,x,c) }, {f↦ λx.λy.λz.d(y,z,c) }, {f↦ λx.λy.λz.d(y,a,c) }, {f↦ λx.λy.λz.d(b,x,c) }, {f↦ λx.λy.λz.d(b,z,c) } and {f↦ λx.λy.λz.d(b,a,c) }. A well studied branch of higher-order unification is the problem of unifying simply typed lambda terms modulo the equality determined by αβη conversions.Gérard Huetgave asemi-decidable(pre-)unification algorithmthat allows a systematic search of the space of unifiers (generalizing the unification algorithm of Martelli-Montanariwith rules for terms containing higher-order variables) that seems to work sufficiently well in practice. Huetand Gilles Dowekhave written articles surveying this topic.

Several subsets of higher-order unification are well-behaved, in that they are decidable and have a most-general unifier for solvable problems. One such subset is the previously described first-order terms.Higher-order pattern unification,due to Dale Miller,is another such subset. The higher-order logic programming languagesλPrologandTwelfhave switched from full higher-order unification to implementing only the pattern fragment; surprisingly pattern unification is sufficient for almost all programs, if each non-pattern unification problem is suspended until a subsequent substitution puts the unification into the pattern fragment. A superset of pattern unification called functions-as-constructors unification is also well-behaved.The Zipperposition theorem prover has an algorithm integrating these well-behaved subsets into a full higher-order unification algorithm.

In computational linguistics, one of the most influential theories ofelliptical constructionis that ellipses are represented by free variables whose values are then determined using Higher-Order Unification. For instance, the semantic representation of "Jon likes Mary and Peter does too" islike(j,m) ∧ R(p)and the value of R (the semantic representation of the ellipsis) is determined by the equationlike(j,m) = R(j).The process of solving such equations is called Higher-Order Unification.

Wayne Snydergave a generalization of both higher-order unification and E-unification, i.e. an algorithm to unify lambda-terms modulo an equational theory.

See also

• Rewriting
• Admissible rule
• Explicit substitutioninlambda calculus
• Mathematicalequation solving
• Dis-unification:solving inequations between symbolic expression
• Anti-unification:computing a least general generalization (lgg) of two terms, dual to computing a most general instance (mgu)
• Subsumption lattice,a lattice having unification as meet and anti-unification as join
• Ontology alignment(useunificationwithsemantic equivalence)

Further reading

• Franz BaaderandWayne Snyder(2001)."Unification Theory"Archived2015-06-08 at theWayback Machine.InJohn Alan RobinsonandAndrei Voronkov,editors,Handbook of Automated Reasoning,volume I, pages 447–533. Elsevier Science Publishers.
• Gilles Dowek(2001)."Higher-order Unification and Matching"Archived2019-05-15 at theWayback Machine.InHandbook of Automated Reasoning.
• Franz Baader andTobias Nipkow(1998).Term Rewriting and All That.Cambridge University Press.
• Franz Baader andJörg H. Siekmann(1993). "Unification Theory". InHandbook of Logic in Artificial Intelligence and Logic Programming.
• Jean-Pierre Jouannaud andClaude Kirchner(1991). "Solving Equations in Abstract Algebras: A Rule-Based Survey of Unification". InComputational Logic: Essays in Honor of Alan Robinson.
• Nachum DershowitzandJean-Pierre Jouannaud,Rewrite Systems,in:Jan van Leeuwen(ed.),Handbook of Theoretical Computer Science,volume BFormal Models and Semantics,Elsevier, 1990, pp. 243–320
• Jörg H. Siekmann (1990). "Unification Theory". InClaude Kirchner(editor)Unification.Academic Press.
• Kevin Knight (Mar 1989)."Unification: A Multidisciplinary Survey"(PDF).ACM Computing Surveys.21(1): 93–124.CiteSeerX10.1.1.64.8967.doi:10.1145/62029.62030.S2CID14619034.
• Gérard HuetandDerek C. Oppen(1980)."Equations and Rewrite Rules: A Survey".Technical report. Stanford University.
• Raulefs, Peter; Siekmann, Jörg; Szabó, P.; Unvericht, E. (1979). "A short survey on the state of the art in matching and unification problems".ACM SIGSAM Bulletin.13(2): 14–20.doi:10.1145/1089208.1089210.S2CID17033087.
• Claude Kirchner and Hélène Kirchner.Rewriting, Solving, Proving.In preparation.