WPGMA

WPGMA(WeightedPairGroupMethod withArithmetic Mean) is a simple agglomerative (bottom-up)hierarchical clusteringmethod, generally attributed toSokalandMichener.

The WPGMA method is similar to itsunweightedvariant, theUPGMAmethod.

Algorithm

The WPGMA algorithm constructs a rooted tree (dendrogram) that reflects the structure present in a pairwisedistance matrix(or asimilarity matrix). At each step, the nearest two clusters, say$i$and$j$,are combined into a higher-level cluster$i\cup j$.Then, its distance to another cluster$k$is simply the arithmetic mean of the average distances between members of$k$and$i$and$k$and$j$:

$d_{(i\cup j),k}={\frac {d_{i,k}+d_{j,k}}{2}}$

The WPGMA algorithm produces rooted dendrograms and requires a constant-rate assumption: it produces anultrametrictree in which the distances from the root to every branch tip are equal. Thisultrametricityassumption is called themolecular clockwhen the tips involveDNA,RNAandproteindata.

Working example

This working example is based on aJC69genetic distance matrix computed from the5S ribosomal RNAsequence alignment of five bacteria:Bacillus subtilis($a$),Bacillus stearothermophilus($b$),Lactobacillusviridescens($c$),Acholeplasmamodicum($d$), andMicrococcus luteus($e$).

First step

• First clustering

Let us assume that we have five elements$(a,b,c,d,e)$and the following matrix$D_{1}$of pairwise distances between them:

	a	b	c	d	e
a	0	17	21	31	23
b	17	0	30	34	21
c	21	30	0	28	39
d	31	34	28	0	43
e	23	21	39	43	0

In this example,$D_{1}(a,b)=17$is the smallest value of$D_{1}$,so we join elements$a$and$b$.

• First branch length estimation

Let$u$denote the node to which$a$and$b$are now connected. Setting$\delta (a,u)=\delta (b,u)=D_{1}(a,b)/2$ensures that elements$a$and$b$are equidistant from$u$.This corresponds to the expectation of theultrametricityhypothesis. The branches joining$a$and$b$to$u$then have lengths$\delta (a,u)=\delta (b,u)=17/2=8.5$(see the final dendrogram)

• First distance matrix update

We then proceed to update the initial distance matrix$D_{1}$into a new distance matrix$D_{2}$(see below), reduced in size by one row and one column because of the clustering of$a$with$b$. Bold values in$D_{2}$correspond to the new distances, calculated byaveraging distancesbetween each element of the first cluster$(a,b)$and each of the remaining elements:

$D_{2}((a,b),c)=(D_{1}(a,c)+D_{1}(b,c))/2=(21+30)/2=25.5$

$D_{2}((a,b),d)=(D_{1}(a,d)+D_{1}(b,d))/2=(31+34)/2=32.5$

$D_{2}((a,b),e)=(D_{1}(a,e)+D_{1}(b,e))/2=(23+21)/2=22$

Italicized values in$D_{2}$are not affected by the matrix update as they correspond to distances between elements not involved in the first cluster.

Second step

• Second clustering

We now reiterate the three previous steps, starting from the new distance matrix$D_{2}$:

	(a,b)	c	d	e
(a,b)	0	25.5	32.5	22
c	25.5	0	28	39
d	32.5	28	0	43
e	22	39	43	0

Here,$D_{2}((a,b),e)=22$is the smallest value of$D_{2}$,so we join cluster$(a,b)$and element$e$.

• Second branch length estimation

Let$v$denote the node to which$(a,b)$and$e$are now connected. Because of the ultrametricity constraint, the branches joining$a$or$b$to$v$,and$e$to$v$are equal and have the following length: $\delta (a,v)=\delta (b,v)=\delta (e,v)=22/2=11$

We deduce the missing branch length: $\delta (u,v)=\delta (e,v)-\delta (a,u)=\delta (e,v)-\delta (b,u)=11-8.5=2.5$(see the final dendrogram)

• Second distance matrix update

We then proceed to update the$D_{2}$matrix into a new distance matrix$D_{3}$(see below), reduced in size by one row and one column because of the clustering of$(a,b)$with$e$: $D_{3}(((a,b),e),c)=(D_{2}((a,b),c)+D_{2}(e,c))/2=(25.5+39)/2=32.25$

Of note, thisaverage calculationof the new distance does not account for the larger size of the$(a,b)$cluster (two elements) with respect to$e$(one element). Similarly:

$D_{3}(((a,b),e),d)=(D_{2}((a,b),d)+D_{2}(e,d))/2=(32.5+43)/2=37.75$

The averaging procedure therefore gives differential weight to the initial distances of matrix$D_{1}$.This is the reason why the method isweighted,not with respect to the mathematical procedure but with respect to the initial distances.

Third step

• Third clustering

We again reiterate the three previous steps, starting from the updated distance matrix$D_{3}$.

	((a,b),e)	c	d
((a,b),e)	0	32.25	37.75
c	32.25	0	28
d	37.75	28	0

Here,$D_{3}(c,d)=28$is the smallest value of$D_{3}$,so we join elements$c$and$d$.

• Third branch length estimation

Let$w$denote the node to which$c$and$d$are now connected. The branches joining$c$and$d$to$w$then have lengths$\delta (c,w)=\delta (d,w)=28/2=14$(see the final dendrogram)

• Third distance matrix update

There is a single entry to update: $D_{4}((c,d),((a,b),e))=(D_{3}(c,((a,b),e))+D_{3}(d,((a,b),e)))/2=(32.25+37.75)/2=35$

Final step

The final$D_{4}$matrix is:

	((a,b),e)	(c,d)
((a,b),e)	0	35
(c,d)	35	0

So we join clusters$((a,b),e)$and$(c,d)$.

Let$r$denote the (root) node to which$((a,b),e)$and$(c,d)$are now connected. The branches joining$((a,b),e)$and$(c,d)$to$r$then have lengths:

$\delta (((a,b),e),r)=\delta ((c,d),r)=35/2=17.5$

We deduce the two remaining branch lengths:

$\delta (v,r)=\delta (((a,b),e),r)-\delta (e,v)=17.5-11=6.5$

$\delta (w,r)=\delta ((c,d),r)-\delta (c,w)=17.5-14=3.5$

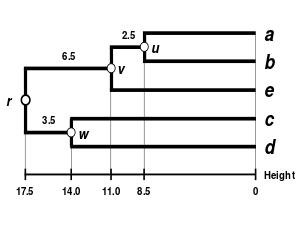
The WPGMA dendrogram

WPGMA Dendrogram 5S data

The dendrogram is now complete. It is ultrametric because all tips ($a$to$e$) are equidistant from$r$:

$\delta (a,r)=\delta (b,r)=\delta (e,r)=\delta (c,r)=\delta (d,r)=17.5$

The dendrogram is therefore rooted by$r$,its deepest node.

Comparison with other linkages

Alternative linkage schemes includesingle linkage clustering,complete linkage clustering,andUPGMA average linkage clustering.Implementing a different linkage is simply a matter of using a different formula to calculate inter-cluster distances during the distance matrix update steps of the above algorithm. Complete linkage clustering avoids a drawback of the alternative single linkage clustering method - the so-calledchaining phenomenon,where clusters formed via single linkage clustering may be forced together due to single elements being close to each other, even though many of the elements in each cluster may be very distant to each other. Complete linkage tends to find compact clusters of approximately equal diameters.

Comparison of dendrograms obtained under different clustering methods from the samedistance matrix.

Single-linkage clustering	Complete-linkage clustering	Average linkage clustering: WPGMA.	Average linkage clustering:UPGMA

See also

• Neighbor-joining
• Molecular clock
• Cluster analysis
• Single-linkage clustering
• Complete-linkage clustering
• Hierarchical clustering