Areo

Areo(komparu:sanskriteur, urv, urw.ars(tero);latinearea(arvum,kampo))estas lakvantoesprimanta la grandecon de regiono surebenoaŭ, pli ĝenerale,mezuronde (ne nepre ebena) dudimensiasurfaco.

Ekzemple, la areo deortanguloestas kalkulata per la formuloa×b,kieakajbestas lalongokaj lalarĝode la ortangulo.

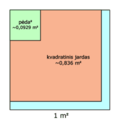
LaSI-unuode areo estaskvadrata metro(m²). Aliaj unuoj estas kvadratakilometroktp. kajhektaro(100 m × 100 m = 10 000 m²).

La vortonareooni uzas ankaŭ en alia senco: tiel oni nomas parton de latera surfacokun difinitajlimojaŭ difinita uzo. Kutime estas klare, ĉu temas pri la areo mem aŭ pri la mezuro de ĝia grando, tamen oni konsciu, ke temas pri la uzado de la sama vorto por malsamaj nocioj.

Difinoj

LaŭFrancisko AzorínareoestasTersurfaco. Spaco inter difinitaj limoj.

Alproksimiĝo al difino de tio kio estas komprenata per "areo" estas kreita traaksiomoj."Areo" povas esti difinita kiel funkcio el kolekto M de speciala tipo de ebenaj figuroj (terminigite kiel mezureblaj surfacoj) al la serio dereelaj nombroj,kio plenumas la jenajn proprecojn:

• Por ĉiuSenM,a(S) ≥ 0.
• SeSkajTestas enMtiam estas ankaŭS∪TkajS∩T,kaj ankaŭa(S∪T) =a(S) +a(T) −a(S∩T).
• SeSkajTestas enMkunS⊆TtiamT−Sestas enMkaja(T−S) =a(T) −a(S).
• Se serioSestas enMkajSestas kongrua kunTtiamTestas ankaŭ enMkaja(S) =a(T).
• Ĉiu ortanguloRestas enM.Se la ortangulo havas longonhkaj larĝonktiama(R) =hk.
• LasuQesti serio ene de inter du ŝtupregionojSkajT.Ŝtupregiono estas formata el finita unio de apudaj ortanguloj restantaj sur komuna bazo, t.e.S⊆Q⊆T.Se estas unika nombroctiel kea(S) ≤ c ≤a(T) por ĉiuj tiaj ŝtupregionojSkajT,tiama(Q) =c.

Oni povas pruvi, ke tia areofunkcio fakte ekzistas.

Historio

La ideo ke la areo estas la mezuro kiu havigas la grandon de la regiono enmetita engeometriaj figurojdevenas de laAntikveco.En laantikva Egipto,post la ĉiujara kreskiĝo fare de la riveroNilokiu inundis la kampojn, aperis la neceso kalkuli la areon de ĉiu agrikultura terpeco por restaŭri ties limojn; por solvi tion, la egiptoj inventis lageometrion,laŭHerodoto.

La maniero kalkuli la areon deplurlaterokiel la adicio de la areoj de trianguloj, estas metodo kiu estis proponita por la unua fojo fare de la greka fakuloAntifonoĉirkaŭ la jaro 430 a.n.e. Kalkuli la areon de kurba figuro generas plian malfacilecon. La elĉerpa metodo konsistas en la enmeto de plurlateroj en la geometria figuro, pligrandigi la nombron de flankoj de tiuj plurlateroj kaj kalkuli la celitan areon. Per tiu sistemo konata kielelĉerpa metododeEŭdokso,oni sukcesis atingi alproksimigon por kalkuli la areon dedisko.Tiu sistemo estis uzata poste fare deArkimedopor solvi aliajn similajn problemojn,same kiel la proksimuman kalkulon de lanombro π.

Area de ebenaj figuroj

Pli detalaj informoj troveblas en artikoloGeometria figuro.

Areo de triangulo

Kalkulo de la areo de triangulo$A={\tfrac {b\cdot h}{2}}$

Areoj enkvadratita papero.

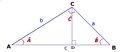
• La areo detrianguloestas egala al la duon-produtointer la longo de unu bazo kaj la alto relativa al tiu:

$A={\frac {b\cdot h}{2}}$

kiebestas la bazo de la triangulo kajhestas la alto koresponda al tiu bazo (oni povas konsideri ajnan lateron kiel bazo).

• Se latriangulo estas orta,la alto koincidas kun unu el lakatetoj,pro kio la areo estas egala al la duonproduto de la katetoj:

$A={\frac {a\cdot b}{2}}$

kieakajbestas la katetoj.

• Se oni konas la longon de ties lateroj, oni povas apliki laformulon de Heron.

$A={\sqrt {s(s-a)(s-b)(s-c)}}$

kiea,b,cestas la valoroj de la longoj de ties lateroj,s= ½ (a+b+c) estas laduonperimetrode la triangulo.

• Se latriangulo estas egallatera,la areo estas egala al unu kvarono de la kvadrato de unu latero por lakvadrata radikode 3:

$A={\frac {{\sqrt {3}}\cdot a^{2}}{4}}$

kieaestas unu latero de la triangulo.

Area de kvarlatero

Trapezoido.

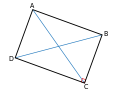
• La areo detrapezoidoaŭ de ajnakvarlateroestas egala al la duonproduto de ties diagonaloj por lasinusode la angulo kiun ili formas.

$A={\frac {{\overline {AC}}\cdot {\overline {BD}}\cdot \sin \theta }{2}}$

La areo estas atingebla ankaŭ pere detriangulado:

$A={\frac {a\cdot d\cdot \sin \alpha +b\cdot c\cdot \sin \gamma }{2}}$

Estante:

$\alpha \,$la angulo inter la lateroj$a\,$kaj$d\,$.

$\gamma \,$la angulo inter la lateroj$b\,$kaj$c\,$.

• Laortanguloestas plurlatero kies anguloj estas ĉiuj de 90º, kaj la areao estas egala al la produto de du el ties sinsekvaj laterojakajb:

$A={a\cdot b\,}$

• Laromboestas plurlatero kies 4 lateroj estas egalaj, kaj ties areo estas la duonproduto de ties du diagonaloj:

$A={\frac {{\overline {AC}}\cdot {\overline {BD}}}{2}}$

• Lakvadratoestas la regula plurlatero de kvar lateroj; ĝi estas samtempe ortangulo kaj rombo, pro kio ĝia areo povas estis kalkulata sammaniere kiel tiuj de la ortangulo kaj de la rombo. Partikulare, ĉar ties lateroj estas egalaj, oni uzas la formulon:

$A=a\cdot a\,=a^{2}$

• Laromboidohavas areon kalkuleblan el la produto de unu de ties lateroj por la respektivaalto:

$A=b\cdot h\,$

• Latrapezo,kiu havas du malajn laterojn paralelajn inter si kaj aliajn du neparalelajn laterojn, havas areon havigitan per la duonproduto de ties paralelaj lateroj multobligita por la distanco inter ili (alto):

$A={\frac {a+b}{2}}\cdot h$

La areo de trapezo povas esti kalkulita kiel longo de la meza linio multiplikita per la distanco laŭperpendikularointer la paralelaj lateroj. Ĉi tio donas kiel speciala okazo la konatan formulon por la areo detriangulo,per konsidero de triangulo kieldegeneratrapezo ĉe kiu unu el la paralelaj lateroj estas malpligrandigita en punkton. Tial, seakajbestas la du paralelaj lateroj kajhestas la distanco (alto) inter la paralelaj lateroj, la area formulo estas:

A= (a+b)h/2

Areo de la disko kaj de la elipso

La areo dedisko,nome tiu limigita decirklo,estas kalkulebla pere de la jena matematika esprimo:

$A=\pi r^{2}\,$

La areo limigita inter la bildo de du kurboj estas kalkulebla pere de la diferenco inter la integraloj de ambaŭ funkcioj.

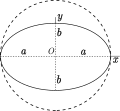
La areo limigita deelipsoestas simila kaj akirebla kiel produto de la duono de la plej granda akso por la duono de la malplej granda akso multobligitaj por π:

$A={\ \pi ab}$

Areo limigita inter du funkcioj

Metodo por atingi la areon limigita inter dufunkcioj,estas uzante laintegralan kalkulon:

${\text{Areo}}(a,b)=\int _{a}^{b}|f(x)-g(x)|dx$

La rezulto de tiu integralo estas la areo enhavita inter la kurboj:$f(x)\,$kaj$g(x)[<f(x)]\,$en la intermezo$[a,b]\,$.

Ekzemplo

Se oni deziras trovi la areon limigitan inter la akso x kaj la funkcio$f(x)=4-x^{2}$en la intermezo$[-2;2]$,oni uzas la antaŭe menciitan ekvacion, tiuokaze:$g(x)=0$tiam pritaksante la integralon, oni akiras jenon:

$A(-2,2)=$$\int _{-2}^{2}|4-x^{2}-0|dx=$$2\int _{0}^{2}4-x^{2}dx=$$2\left[4x-{\cfrac {x^{3}}{3}}\right]_{0}^{2}=$$2\left[8-\left({\cfrac {2^{3}-0}{3}}\right)\right]=$${\cfrac {32}{3}}$

Pro kio oni konkludas, ke la areo limigita estas$32/3$.

Ankaŭ lavolumenoenfermita inter du funkcioj povas esti atingebla per la kalkulo de simila integralo.

Rilato areo-perimetro

Difinita simpla kurbo enfermita en la eŭklida ebeno, oni povas pruvi, ke ties longo aŭperimetrode la areo enfermita kaj la propra areo enfermita kongruas kun la rilato:

${\frac {A}{L^{2}}}\leq {\frac {1}{4\pi }}$

La egaleco estas atingebla nur por disko; la ceteraj figuroj kaj eblaj formoj plenumas plej striktan malegalecon.

Disvastiĝa areo

Disvastiĝa areoestas esprimo por difini tiun teran surfacon de bestospecioj, kiun ili konkeris, tie ili disvastiĝis. Por tiu koncepto oni uzas ankaŭ laterminonarealo.

Bildaro

• 
  Komparoj de kvadratafutokaj kvadratajardokun kvadratametro.
• 
  La areo de ortangulo estas la produto de la longo kaj la larĝo
• 
  La areo dekvadratoestas lakvadratode lalaterolongo
• 
  La areo detrianguloestas la duono de la produto de la latero kaj laaltorilata al tiu latero
• 
  La aero deelipso=$\pi ab$;la aero de lacirklo=$\pi a^{2}$

Literaturo

• Spiegel, Murray R.; Abellanas, Lorenzo (1992). McGraw-Hill, eld.Fórmulas y tablas de matemática aplicada.Aravaca (Madrid).ISBN 84-7615-197-7.

Eksteraj ligiloj

• http://www.shurey.com/Soft/JavaScript/DoRyouKou/square.html ( Areo )
• En tiu ĉi artikolo estas uzita traduko de teksto el la artikoloÁreaen la hispana Vikipedio.