Dulatero

Degenera dulatero kun du koincidantaj lateroj kunigantaj du la samajn verticojn

Engeometriodulateroestasplurlaterokun dulaterojkaj duverticoj.

Dulatero devas estiregulaĉar ĝiaj du randoj estas la sama longo. Ĝi havassimbolo de Schläfli{2}.

Eneŭklida ebenokajhiperbola ebenodulatero estas ĉiamdegenera(kun nula enaareo).

Sur sfero

Sursfero(ensfera geometrio), nedegenera dulatero povas ekzisti se la verticoj estasantipodaj punktoj.Tiela dulatero estas ankaŭ nomatalunoaŭŝpino.Tiam ĝiaj lateroj estas duonoj de duĉefcirkloj.Laena angulode la sfera dulatera vertico povas esti ĉiu angulo inter 0 kaj 2π (aŭ 360 gradoj). (Oni povas ankaŭ difini lunon kiel parto desferasurfacokunmetita inter duduonplanojkiuj eliras de unudiametrode l' sfero.)

La areo de ĉi tiu dulatero estas

2R²α,

kieRestasradiusode la sfero,

α estas laena anguloĉe ĉiu el verticoj (aŭ laduedra angulo,se oni difinas dulateron per duonplanoj). Se ĉi tiu angulo egalas al 2π la luno kovras la tutan sferon kaj la area formulo por la sfera luno donas4πR²kio estas la surfaca areo de la tuta sfero.

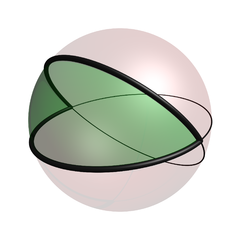Unu nedegenera dulatero sur sfero. La duĉefcirklojestas montrita kiel maldikaj nigraj linioj, la luno (montrita en verda) estas konturigita per dikaj nigraj linioj, respektivaj al ĝiaj difinantaj duonoj de ĉefcirkloj. La ĉefcirkloj intersekciĝas je du polusaj kontraŭaj punktoj.

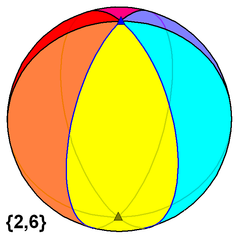Ses dulateroj de seslateraduvertica pluredro.La duvertica pluredro estaskahelarode la sfero.

Lumanta kaj malhela partoj de laLuno(astronomio). En diversaj tempoj eblas ambaŭ variantoj je tio kiu el la du partoj estas lumanta kaj kiu estas malhela.

La lumanta videbla parta de laLuno(astronomio) estas sfera luno. La unua el la du intersekcantaj ĉefcirkloj estas la rando apartiganta la lumantan duonon de la Luno de la malhela duono. La dua ĉefcirklo estas tiu kiu apartigas la duonon videblan de laTerode la nevidebla duono. Vidataorta projekciode ĉi tiu sfera luno havas unuon el la arkojelipsan.

En pluredroj

Dulatero estas konsiderata kiel degeneriedrodepluredro,sed ĝia topologia ekzisto povas iam esti utila en konvertadoj de pluredroj.

Ĉiupluredropovas esti topologie modifita per anstataŭigo de latero per dulatero. Ĉi tiu operacio adicias unu lateron kaj unu edron al la pluredro, kvankam la rezulto estas geometrie identa. Ĉi tiu transformo ne ŝanĝas laeŭleran karakterizon(χ=V-L+E).

Dulatero kiel edro povas ankaŭ kreiĝi per geometria kolapsigo dekvarlateraedro per movo de paroj de verticoj al koincido en la spaco. Ĉi tiu dulatero povas tiam esti anstataŭigita per sola latero. Tiam la pluredro perdas unu edron, du verticoj, kaj tri laterojn, ne ŝanĝante laeŭleran karakterizon.

Vidu ankaŭ

• Duedro- degenera pluredro kun 2 edroj.
• Duvertica pluredro- degenera pluredro kun 2 verticoj.

Referencoj

• Eric W. Weisstein,DulateroenMathWorld.
• [1]A. B. Ivanov enEnciklopedio de matematikopri dulatero (ISBN 978-1-55608-010-4)