Pitagóricos

Grupo de pitagóricos celebrando la salida del sol.
Himno al sol naciente,Fyodor Bronnikov(1827-1902;óleo).

Elpitagorismofue un movimientofilosófico-religiosode mediados del sigloVIa. C. fundado porPitágoras de Samos,siendo ésta la razón por la cual sus seguidores recibían el nombrepitagóricos.Estos formaban laescuela pitagórica,​ agrupación osecta​ conformada porastrólogos,músicos,matemáticosyfilósofoscuya creencia más destacada era que todas las cosas son, en esencia,números.

Algunos de estos fueronEpicarmo de Megara,Alcmeón de Crotona,Hipaso de Metaponto,Filolao de CrotonayArquitas de Tarento.El filósofoJámblico de Calcisconfeccionó un supuestocatálogo de los pitagóricos.

Este movimiento descubrió losnúmeros irracionales,​ aunque obligaba a sus seguidores a que lo mantuvieran en secreto. Se cree que el pitagóricoHipaso de Metapontoreveló el secreto y, según la leyenda, fue ahogado por no mantenerlo.​

Elpentagrama(estrella de cinco puntas) fue un importante símbolo religioso usado por los pitagóricos, que lo denominaban «salud».

Cosmología pitagórica

Busto dePitágoras

El pensamiento pitagórico estaba dominado por lasmatemáticas,a la vez que era profundamente místico. En el área de lacosmologíano hay acuerdo sobre si el mismoPitágorasimpartía enseñanzas, pero muchos eruditos creen que la idea pitagórica de latransmigración del almaes demasiado importante para haber sido añadida por un seguidor posterior a Pitágoras. Por otra parte, es imposible determinar el origen de la doctrina pitagórica de la sustancia. Parece que la doctrina pitagórica parte de la doctrina deAnaximandrosobre la última sustancia de las cosas como "lo ilimitado". Un pupilo de Anaximandro,Anaxímenes,contemporáneo de Pitágoras, dio una explicación de cómo lo "ilimitado" según Anaximandro tomó forma, por condensación y rarefacción. Por otra parte, la doctrina pitagórica dice que mediante la noción de "límite" lo "ilimitado" toma forma.

Diógenes Laercio(sobre 200 d. C.) cita el libroSucesiones de Filósofosde Alejandro Polyhistor (sobre 100 aC). Según Diógenes, Alejandro tuvo acceso a un libro llamadoLa memoria pitagóricaen su relato de cómo fue construida la cosmología pitagórica:

El principio de todas las cosas es lamónadao unidad; de esta mónada nace la dualidad indefinida que sirve de sustrato material a la mónada, que es su causa; de la mónada y la dualidad indefinida surgen los números; de los números, puntos; de los puntos, líneas; de las líneas, figuras planas; de las figuras planas, cuerpos sólidos; de los cuerpos sólidos, cuerpos sensibles, cuyos componentes son cuatro: fuego, agua, tierra y aire; estos cuatro elementos se intercambian y se transforman totalmente el uno en el otro, combinándose para producir un universo animado, inteligente, esférico, con la tierra como su centro, y la tierra misma también es esférica y está habitada en su interior. También hay antípodas, y nuestro ‘abajo' es su ‘arriba'.

Diógenes Laercio,Vitae philosophorum VIII,15.

Esta cosmología inspiró algnósticoárabeMonoimus,que combinó este sistema con elmonismoy otros aspectos de su propia cosmología.

Basándose en la especulación matemática y en las propiedades y relaciones que atribuían a los números, los pitagóricos postularon unsistema astronómiconovedoso. Dedujeron que la fuerza divina debe configurarlo ilimitadodesde el centro delcosmos,por lo que laTierra—al igual que el resto de cuerpos celestes— se movería alrededor de esefuego central.De esta manera, propusieron la primera explicación documentada del movimiento aparente de labóveda celestepor un movimiento de la Tierra. Mediante estemodelo no geocéntrico,en el seno de esta escuela filosófica se desarrollaron las teorías detraslaciónyrotaciónen torno a su eje de nuestro planeta.​

Desarrollo histórico

Después de los milesios, el siguiente movimiento filosófico importante (cronológicamente hablando) fueron los pitagóricos. Tras las luchas políticas de mediados del sigloVIa. C., la escuela pitagórica fundada en Crotona (Italia) fue destruida y la emigración de los pitagóricos y de sus doctrinas se realiza hacia la metrópoli, donde hacia esa época comenzaron a difundirse. Dos corrientes aparecen entonces: los "matemáticos" ('conocedores', en griego) y los "acusmáticos" ('oidores', en griego);​ los primeros eran partidarios de renovar las doctrinas de Pitágoras; los segundos eran fundamentalistas: solo querían conservar la doctrina del maestro tal cual, sin cambiarla y aprendiéndola de memoria sin discutirla.​ A fines del sigloVIa. C. la filosofía se traslada de las costas de Jonia a las de la Magna Grecia, al sur de Italia y a Sicilia, y se constituye lo queAristótelesllamó laescuela itálica.

Bartel Leendert van der Waerdendistingue cinco generaciones en el pitagorismo matemático entre los años 530-360.

• 1.ª Generación (530-500):Pitágoras.
• 2.ª Generación (520-480):Hípaso de Metaponto,Alcmeón de Crotona.
• 3.ª Generación (480-430): Matemáticos anónimos.
• 4.ª Generación (440-400):Filolao,Teodoro de Cirene.
• 5ª Generación (400-360):Arquitas de Tarento.​

Especialmente afamada fue la III.ª generación. De ellos decía Aristóteles (segúnJámblico,Περὶ τῆς κοινῆς μαθηματικῆς ἐπιστήμης / De communi Mathematica scientia,78) que «estiman mucho la exactitud de la argumentación en las ciencias matemáticas, porque solo ellas poseen demostraciones». Dejó una fuerte huella en la geometría y en la aritmética que quedó reflejada en losElementosdeEuclides.

Misticismo y ciencia

Pocos rasgos hay que distingan aquí al pitagorismo de una simplereligiónmística,pero los pitagóricos figuraban, en el sigloVI,entre los principales investigadores científicos. Pitágoras se interesó tanto por lacienciacomo por el destino delalma.La religión y la ciencia no eran para él dos compartimentos separados sin contacto alguno, sino más bien constituían los dos factores indisociables de un único estilo de vida.

Las nociones fundamentales que mantuvieron unidas las dos ramas que más tarde se separaron parecen haber sido las decontemplación,el descubrimiento de unordenen la disposición deluniversoy la necesidad depurificación.

Mediante la contemplación del principio de orden manifestado en el universo, especialmente en los movimientos regulares de los cuerpos celestes, y asemejándose asimismo a ese orden, se fue purificando progresivamente el hombre hasta terminar por liberarse de lametempsicosiso ciclo de reencarnaciones y adquirir lainmortalidad.

Biografía de Pitágoras

Pitágorasen una moneda

Véase también:Pitágoras

Pitágoras nace en el 570 a. C. proveniente del Asia menor (isla deSamos). Más tarde se traslada aCrotonaal ser desterrado porPolícrates de Samos.Se le atribuyen varios viajes a Oriente, entre otros aPersia,donde hubo de conocer al mago Zaratás, es decir, aZoroastroo Zaratustra. De los egipcios heredó la Geometría y el arte de la adivinación; de los fenicios aprendió la aritmética y el cálculo, y de los caldeos la investigación de los astros.

Del Pitagorismo al Neopitagorismo

Véase también:Neopitagorismo

Los pitagóricos se establecieron en una serie de ciudades de la Italia continental y deSicilia,y luego pasaron también a la Grecia propia. Formaron una liga o secta, y se sometían a una gran cantidad de extrañas normas y prohibiciones; no comían carne ni habas, ni podían usar vestido de lana, ni recoger lo que se había caído, ni atizar el fuego con un hierro, etc. Resulta difícil comprender el sentido de estas normas, si es que tenían alguno.

Algunos comentaristas tardíos comoSan Hipólitodel sigloIIIrefieren que los adeptos se distinguían entre sí como novicios o iniciados. Los primeros solo podían escuchar y callar (exotéricosyacústicos) mientras que los segundos (esotéricoso matemáticos) podían hablar y expresar lo que pensaban acerca de las cuestiones científicas de las que se ocupaba la escuela.

La liga pitagórica tenía una tendencia contraria a laaristocracia;pero acabó por formar una e intervenir en la política de las ciudades-estado de la época. Como consecuencia de esto, se produjo una violenta reacción democrática enCrotona,y los pitagóricos fueron perseguidos, muchos de ellos muertos, y su casa incendiada. El fundador logró salvarse y murió, según se dice, poco después. Más tarde alcanzaron los pitagóricos un nuevo florecimiento, llamado elneopitagorismo,basándose en aplicar la mente a los resultados dados por los conocimientos pitagóricos.

Filósofos pitagóricos

Véase también:Mujeres filósofas

Como era habitual en aquel tiempo, todos los escritos de los miembros de la Escuela eran atribuidos a Pitágoras. La mayoría de los seguidores de esta eran hombres, comoEpicarmo de Megara,Alcmeón de Crotona,Hipaso de Metaponto,Filolao de CrotonayArquitas de Tarento.y estos aparecían como los únicos creadores, pero gracias a algunos escritos y a la esposa de Pitágoras, llamadaTéanopudimos saber que también existieron mujeres.​

SegúnDiógenes Laercio,los pitagóricos "entregaron sus mujeres para que aprendiesen sus preceptos; de donde vino que fueron llamadas Pitagóricas".​ En laVida de Pitágoras,el filósofoJámblicoconfeccionó un supuestocatálogo de los Pitagóricoscon un listado de 32 estudiantes de la Escuela Pitagórica, en el que figuran 17 mujeres:​ Timica, Filtide, Ocelo de Laconia, su hermana Ecelo, Quilónide, Cratesiclea de Esparta, Téano,Mía,Lastenia,Habrotelia, Equecratia de Fliunte, Tirsenis, Pisírrode, Teadusa, Boio de Argos, Babélica de Argos y Cleecma. No obstante, a esta lista,Estobeoañade otras tres conocidas figuras femeninas del pitagorismo, comoFintis,Melisa de SamosyPerictione.La pitagóricaMelisafue mencionada porGilles MénageenHistoria de las mujeres filósofas.​

Doctrina

Constituía propiamente una escuela (engriegoescuela significaocio). Esta escuela está definida por un modo de vivir de sus miembros, personas emigradas, expatriadas; forasteros, en suma. Según el ejemplo de los juegos olímpicos, hablaban los pitagóricos de tres modos de vida: el de los que van a comprar y vender, el de los que corren en el estadio y el de los espectadores que se limitan a ver. Así viven los pitagóricos, forasteros curiosos de laMagna Grecia,como espectadores. Es lo que se llama elbios teoretiós,la vida teorética o contemplativa. La dificultad para esta vida es elcuerpo,con susnecesidades,que sujetan al hombre. Es menesterliberarsede esas necesidades. El cuerpo es una tumba (soma sema), dicen los pitagóricos. Hay que superarlo, pero sin perderlo. Para esto es necesario un estado previo delalma,que es el entusiasmo (no debemos pensar lo que actualmente pensamos por entusiasmo, sino que debemos remitirnos al término en griego:ἐνθουσιαζόντoς;este término quiere decir estar lleno de Dios, poseído, pero no en un sentido peyorativo, sino que simplemente la persona presta su ser para que el dios, generalmente lasMusas,hablen por medio de él). Aquí aparece la conexión con losÓrficosy sus ritos, fundados en lamanía(locura) y en laorgía.La escuela pitagórica utiliza estos ritos y los transforma. Así se llega a una vida suficiente, teorética, no ligada a las necesidades delcuerpo,un modo de vivir divino. El hombre que llega a esto es el sabio, elsophós(parece que la palabrafilosofíao "amor a la sabiduría", más modesta queSofía,surgió por primera vez de los círculos pitagóricos). El perfectosophóses al mismo tiempo el perfectopolitésociudadano;por esto el pitagorismo crea unaaristocraciay acaba por intervenir en política.

Los pitagóricos seguían unadietavegetariana​ a la que llamaban por aquel entoncesdieta pitagórica.

Números y figuras geométricas

Véase también:Numeración griega

Pentagrama:lospitagóricosusaron este símbolo como unsigno secretopara reconocerse unos a otros. Representa el númerocinco,lavida,elpodery lainvulnerabilidad.

De entre las numerosas contribuciones matemáticas que se atribuyen a los pitagóricos destacan por su importancia las algebraicas ygeométricas.Filosóficamente, la concepción pitagórica delnúmerolo hacía omnipresente,esenciade todas las cosas.

SegúnNeugebauer,a partir de su interpretación de las tablillas cuneiformes de este siglo, "lo que se llama pitagórico en la tradición griega debería probablemente ser llamadobabilonio",pues los pitagóricos habrían aprehendido sus conocimientos matemáticos en laaritméticay en elálgebrade los babilonios. Más tarde, imprimieron estos conocimientos en su propio estilo con un carácter específicamente griego, anteponiendo al carácter operativo e instrumental de los babilonios el rigorlógicoy lademostración matemática.

Los pitagóricos hacen el descubrimiento de un tipo de entes, losnúmerosy lasfiguras geométricasque no soncorporales,pero que tienenrealidady presentan resistencia alpensamiento;esto hace pensar que no puede identificarse sin más elsercon el ser corporal, lo cual obliga a una decisiva ampliación de la noción delente.Pero los pitagóricos, arrastrados por su propio descubrimiento, hacen una nueva identificación, esta vez de signo inverso: el ser va a coincidir para ellos con el ser de los objetos matemáticos. Los números y lasfigurasson laesenciade las cosas; los entes son por imitación de los objetos de la matemática; en algunos textos afirman que los números son las cosas mismas. La matemática pitagórica no es unatécnicaoperatoria, sino antes que ello el descubrimiento y construcción de nuevos entes, que son inmutables y eternos, a diferencia de las cosas variables y perecederas.

De ahí el misterio de que se rodeaban los hallazgos de la escuela, por ejemplo el descubrimiento de lospoliedrosregulares. Una tradición refiere queHipaso de Metaponto,tras ser repudiado como hereje, fue ahogado durante una travesía o bien naufragó, castigado por los dioses por haber revelado el secreto de la construcción deldodecaedro.

Por otra parte, laaritméticay lageometríaestán en estrecha relación: El 1 es el punto, el 2 la línea (recta), el 3 lasuperficie,el 4 elvolumen;el número 10, suma de los cuatro primeros, es la famosatetraktys,el número capital. Se habla geométricamente de números "cuadrados"y" oblongos "," planos "", "cúbicos",etc. Hay números místicos, dotados de propiedades especiales. Los pitagóricos establecen una serie de oposiciones, con las que las cualidades guardan una extraña relación: loilimitadoy lolimitado,lopary loimpar,lomúltipley louno,etc. El simbolismo de estas ideas resulta problemático y de difícil comprensión.

La escuela pitagórica creó también unateoría matemáticade lamúsica.La relación entre las longitudes de las cuerdas y lasnotascorrespondientes fueron aprovechadas para un estudio cuantitativo de lo musical; se pensó que cada astro da una nota, y todas juntas componen la llamadaarmonía de las esferasomúsica celestial,resonanciaque no oímos por ser constante y sin variaciones.

Inmortalidad del alma

Para los pitagóricos lamuerteera una necesidad que convenía aldevenir(naturaleza) de la vida universal, o como un incómodo bien ante las situaciones de extrema postración humana.

Ante la pregunta de qué es lo que permanece y en dónde, enGreciay enRomase concebía lamuertecomo el paso a una segundaexistencia,y, por tanto, no como una extinción definitiva, sino como un cambio de estado que acontece a algo oculto e invencible. Vale resaltar que en Grecia había, por así decirlo, una religión olímpica politeísta, y otras mistéricas (Orfismo,Ritos eleusinos) en donde se creía que después de la muerte había otra vida, en donde se encontraba la recompensa al sufrimiento de este mundo.

Los pitagóricos tenían una concepción de unidad decuerpo(físico) yalma,en donde el alma después de la muerte se separaba del cuerpo, esa separación era la misma muerte.

Después de la muerte delindividuoel alma, que es una especie desombrafantasmagórica,peregrinaba a través de todo, con el fin de reencarnar sucesivamente en otros cuerpos. Este es el fundamento de lapalingenesia,denominada tambiénmetempsicosisotrasmigración del alma.Por esta razón los pitagóricos no rechazaban ningún estilo de vida, puesto que el alma podía transitar por cualquiera de ellos.

El alma era considerada la antítesis del cuerpo, era el lado de laperfecciónhumana: lo bueno, lo puro, lo racional o lo eterno e incorruptible; mientras que el cuerpo era todo lo que simbolizaba lo malo, lo impuro, lo irracional o lo corruptible.

El número como principio de todas las cosas

Como diceAristóteles,los pitagóricos se dedicaron a lasmatemáticas,fueron los primeros que hicieron progresar este estudio y, habiéndose formado en él, pensaron que sus principios eran los de todas las cosas.

"Nutridos de ella (la matemática), creyeron que su principio fuera el de todas las cosas. Ya que los números por su naturaleza son los primeros que se presentan en ella, les pareció observar en los números semejanzas con los seres y con los fenómenos, mucho más que en el fuego, o en la tierra o en el agua y como también veían en los números las determinaciones y las proporciones de las armonías y como, por otra parte, les parecía que toda la naturaleza estaba por lo demás hecha a imagen de los números, y que los números son los primeros en la naturaleza, supusieron que los elementos de los números fuesen los elementos de todos los seres y que el universo entero fuese armonía y número. Y todas las concordancias que podían demostrar en los números y en las armonías con las condiciones y partes del universo y con su ordenación total, las recogieron y coordinaron."

Aristóteles.

Tenían el entusiasmo propio de los primeros estudiosos de una ciencia en pleno progreso, y les cultivó la importancia del número en el cosmos: todas las cosas son numerables, y muchas las podemos expresar numéricamente. Así la relación entre dos cosas relacionadas se puede expresar por una proporción numérica; el orden existente en una cantidad de sujetos ordenados se puede expresar mediante números, y así sucesivamente. Pero lo que parece que les impresionó más que nada fue el descubrir que los intervalos musicales que hay entre las notas de la lira pueden expresarse numéricamente. Cabe decir que la altura de un sonido depende del número, en cuanto que depende de las longitudes de las cuerdas, y es posible representar los intervalos de la escala con razones numéricas. A partir de esto surge la idea de cantidad (to pason), lo cuantitativo como principio y esencia de la realidad, es decir, que locualitativose determina en locuantitativo.

Pues bien, lo mismo que laarmonía musicaldepende de un número, se puede pensar que laarmonía del universodepende también del número. Los cosmólogos milesios hablan deun conflicto universal de los elementos contrapuestos,y los pitagóricos, gracias a sus investigaciones en el campo de la música, tal vez pensasen solucionar el “conflicto” recurriendo al concepto de número. Según Aristóteles, “como vieron que los atributos y las relaciones de las escalas musicales se podían expresar con números, desde entonces todas las demás cosas les parecieron modeladas en toda su naturaleza según los números, y juzgaron que los números eran lo primero en el conjunto de la naturaleza y que el cielo entero era una escala musical y un número”. Mas lo que uno cree entender de los pitagóricos es que quisieron decir que el carácter verdadero no lo determinaba la apariencia sensible sino que lo establece un componente cuantitativo aritmo–geométrico que está referido tanto al número (cantidad discreta) como a la magnitud (cantidad continua); o sea, que tal ingrediente matemático afecta lacualidadde las cosas.

Este lenguaje matemático no era usado solo para explicar el mundo, también era usado en lasentidades excluidas,las que tenían que ver con lasesferas subjetivas,el hombre, la justicia, el arte, la medicina y hasta las estaciones, pues todo esto requería de números, proporción y medida. El lenguaje de la realidad es entonces para los pitagóricos, unlogosmatemático (razón, armonía y medida).

Anaximandrohabía hecho derivar todo de lo Ilimitado o Indeterminado. Pitágoras combinó esta noción con la de límite, que da forma a lo ilimitado. Ejemplo de todo ello es la música (y también la salud, en la que el límite es la templanza, cuyo resultado es una sana armonía). La proporción y la armonía de los sones musicales son expresables aritméticamente. Transfiriendo estas observaciones al mundo en general, los pitagóricos hablaron de la armonía cósmica. Y, no contentos con recalcar la importancia de los números en el universo, fueron más lejos y declararon quelas cosas son números.

Evidentemente, tal doctrina no es de fácil comprensión. Se hace duro decir que todas las cosas son números. ¿Qué entendían por ello los pitagóricos? En primer lugar, ¿qué entendían por números o qué es lo que pensaban acerca de los números?. Aristóteles nos informa que “los pitagóricos sostenían que los elementos del número son lo par y lo impar, y que, de estos elementos, el primero es ilimitado y el segundo limitado; la unidad, el uno, procede de ambos (pues es a la vez par e impar), y el número procede del uno; y el cielo todo, es números”. Los pitagóricos consideraron los números espacialmente. La unidad es el punto, el dos es la línea, el tres la superficie, el cuatro el volumen. Decir que todas las cosas son números significaría que “todos los cuerpos constan de puntos o unidades en el espacio, los cuales, cuando se los toma en conjunto, constituyen un número”.

La Tetraktys: el número diez

Tetraktys:figura triangularconsistente en diez puntos colocados en cuatro líneas: un, dos, tres, y cuatro puntos en cada fila.Símbolomísticoque representa el númerodiez.

Latetraktys,figura que tenían por sagrada, indica que los pitagóricos consideraban así los números. Esta figura demuestra que el 10 resulta de sumar 1+2+3+4,o sea, que es la suma de los cuatro primero números enteros. Por ella hacían el juramento transmitido como pitagórico, hecho en nombre de Pitágoras mismo, pero sin nombrarlo, “por quién transmitió a nuestra alma la tetraktys”. La tetraktys es el número perfecto y la clave de la doctrina. Es posible que jugase también un papel en los distintos grados de la metamorfosis del alma.

El dieztiene el sentido de la totalidad, de final, de retorno a la unidad finalizando el ciclo de los nueve primeros números. Para los pitagóricos esla santa tetraktys,el más sagrado de todos los números por simbolizar a la creación universal, fuente y raíz de la eterna naturaleza; y si todo deriva de ella, todo vuelve a ella. Es pues una imagen dela totalidad en movimiento.

La tetraktys forma un triángulo de 10 puntos colocados en cuatro líneas, de la forma siguiente:

La Santa Tetraktys pitagórica

1. La Unidad:Lo Divino, origen de todas las cosas. El ser inmanifestado.
2. La Díada:Desdoblamiento del punto, origen de la pareja masculino-femenino. Dualismo interno de todos los seres.
3. La Tríada:Los tres niveles del mundo: celeste, terrestre, infernal, y todas las trinidades.
4. El Cuaternario:los cuatro elementos, tierra, aire, fuego y agua, y con ellos la multiplicidad del universo material.

El conjunto constituyela Década,la totalidad de Universo: 4: 1 + 2 + 3 + 4 = 10 → 1 + 0 = 1.

Todo es Número:el número como explicación de la realidad

Además, los pitagóricos concebían a los números con un carácter pedagógico, pues como ellos no hay otra cosa que tenga mayor capacidad explicativa o transmisora de información. El número tenía un sentido genérico y decisivo en la construcción del cosmos. El comienzo eslo Uno(monas), es indeterminada y de naturaleza divina, semejante alapeirondeAnaximandro.De lo unolimitado(denominado así porque no es aún una dualidad numérica o completa, pues lo uno no es el uno cuantitativo, sino un género supremo), surgela díada indefinida(aoristos duas). Pues de la unión de estos dos surgeel unoyel dos numérico,es decir, de lo uno el uno y de lo uno y de la díada indefinida el dos. Por extensión surgen los demás números.

Lo unodebemos entenderlo comoidentidaden tanto la propiedad que tienen las cosas de ser ellas mismas,la díadadebemos entenderla comolas diferenciaspues es en este pensamiento el que liga la identidad con la diferencia, que asume la unidad y la dualidad como los elementos de lo verdadero.

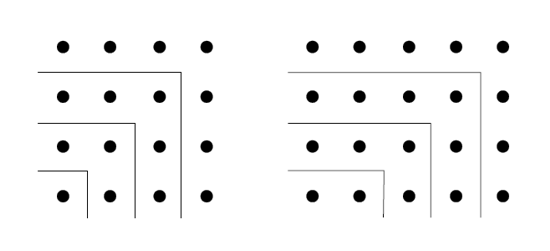
Euritosolía representar los números con piedrecillas, y por este procedimiento, obtenemos los números “cuadrados” y los números “triangulares”.

En efecto, si partimos de la unidad y le añadimos los números impares siguiendo elgnomon,obtendremos los números «cuadrados», mientras que si partimos del 2 y le añadimos los números pares, obtendremos los números «oblongos»:

Esta costumbre de representar los números o relacionarlos con la geometría ayuda a comprender por qué los pitagóricos consideraban las cosas como números y no solo como numerables: transferían sus concepciones matemáticas al orden de la realidad material. Por la yuxtaposición de puntos se engendra la línea, la superficie es engendrada por la yuxtaposición de varias líneas y el cuerpo por la combinación de superficies. Puntos, líneas y superficies son las unidades reales que componen todos los cuerpos de la naturaleza, y en este sentido todos los cuerpos deben ser considerados como números. Cada cuerpo material es una expresión del número cuatro, puesto que resulta como un cuarto término de tres clases de elementos constitutivos: puntos,líneasysuperficies(Véase tambiénDimensión).

Noción de límite y armonía

Véase también:Armonía de las esferas

Para los pitagóricos, elcosmoslimitado, omundo,está rodeado por el inmenso o ilimitado cosmos (elaire), y aquel lo “inhala”. Los objetos del cosmos limitado, no son, pues, pura limitación, sino que tienen mezcla de lo ilimitado. Los pitagóricos al considerar geométricamente los números, los concebían también como productos de lo limitado y lo ilimitado (por estar compuestos delo par y lo impar). Identificándose el par con lo ilimitado y lo impar con lo limitado. Una explicación complementaria puede verse en el hecho de que los gnómones impares conservan su forma cuadrada fija (limitada), mientras que los pares presentan una forma rectangular siempre cambiante (ilimitada).

Para los Pitagóricos, latierra era esférica.La tierra y losplanetasgiraban a la vez que elsolen torno al fuego central o “corazón del Cosmos”, identificado con el número uno (véaseSistema astronómico pitagórico).

Para ellos la esencia de las cosas erala Armonía de los contrarios,lo cual constituíaellímiteque determina el ser preciso de las cosas en tanto que todo ser lo es dentro de determinados acontecimientos figuradores. La forma, progresión,armoníacorporal no son caprichosas sino que son reglas que se ajustan a determinadas medidas proporcionales, pues el límite es control ante los desmanes, la cordura frente a las pretensiones desmedidas. Así, de esta manera,el límiteconstituíaelequilibrioyla armonía,la fuerza que unía los contrarios.Estas ideas influyeron considerablemente en el estudio de lamedicina en la Antigua Greciay hasta la Edad Media, pues se consideraba que la salud de cada individuo dependía de una combinación correcta (krasis) de elementos físicos opuestos (calor-frío, sequedad-humedad), los cuales debían guardar o recuperar —en caso de enfermedad— laarmoníacorporal. Dicha doctrina se convirtió en fundamental para la medicina griega, iniciada por el pitagóricoAlcmeón de Crotona.​

Crisis del racionalismo numérico

Los pitagóricos descubrieron losnúmeros irracionales,​ se trataba del hallazgo delo irracional,dela raíz cuadrada de dos,aplicable ala relación, mediante su famoso teorema, entre los lados de un cuadrado y su diagonal.

En la literatura

• En la novelaLa espada de fuego(2003) deJavier Negretelos numeristas están inspirados en los pitagóricos.
• La novelaEl asesinato de Pitágoras(2013) describe cómo pudo haber sido la sociedad pitagórica, según la visión dramatizada del autor,Marcos Chicot.

Véase también

• Anexo:Catálogo de pitagóricos de Jámblico
• Afinación pitagórica
• Armonía de las esferas
• Número triangular
• Teorema de Pitágoras
• Ecuación pitagórica
• Sistema astronómico pitagórico
• Terna pitagórica
• Filosofía antigua, misterios y magia

Bibliografía

• Aguilera, Julián María (1985).Historia de la Filosofía.Madrid: Editorial Alianza S. A.
• Copleston, Frederick C.(2004).Historia de la Filosofía. Tomo 1/I: Grecia y Roma.Editorial Ariel: Barcelona.ISBN 84-344-8770-5.
• Eggers Lan, Conrado y Victoria E. Juliá (2000 [1ª edición, 4ª impresión]).Los filósofos presocráticos. Tomo I.Editorial Gredos:Madrid.ISBN 84-249-3511-X.
• Ferrater Mora, J (1941).Diccionario de Filosofía.Editorial Ariel S. A.
• Fraile, Guillermo y Urdánoz, Teófilo (1926 [4ª edición]).Historia de la Filosofía I.Madrid: Editorial Católica S. A.
• Guthrie, W.K.C., (1999 [1ª edición, 3ª reimpresión]).Historia de la Filosofía Griega. Vol. I: Los primeros presocráticos y los pitagóricos.Editorial Gredos: Madrid.ISBN 84-249-0949-6.
• Jámblico(2003).Vida pitagórica. Protréptico.Madrid: Editorial Gredos.ISBN 978-84-249-2397-6.
• Kirk, G.S., Raven, J.E., y Schofield, M (2008).Los filósofos presocráticos. Historia crítica con selección de textos.edición revisada, tapa dura. Madrid: Editorial Gredos.ISBN 978-84-249-3567-2.
• Kornél Zoltán Méhész (1974). "Pythagoras". Arg.: Univ.Nac. Nordeste.
• O'Meara, Patrick J (1989).Pythagoras Revived.Clarendon Press, Oxford.
• Osorio, Amado (2001).Introducción a la Filosofía presocrática.Editorial Universidad de Caldas, Manizales.
• Porfirio(1987 [1ª edición, 2ª impresión]).Vida de Pitágoras. Argonaúticas Órficas. Himnos Órficos.Madrid: Editorial Gredos.ISBN 978-84-249-1234-5.
• Rey Pastor, J. (1997).Historia de la Matemática. Vol. 1.Editorial Gedisa, Barcelona.ISBN 84-7432-207-3.
• VV.AA. (1998).Diccionario Enciclopédico Temático Brújula.Editorial Norma, S.A., Bogotá.
• VV.AA. (1945 [2ª edición]).Diccionario Enciclopédico Salvat. Tomo VII.Editorial Salvat Editores S.A., Barcelona/Buenos Aires.

Enlaces externos

• Pitágoras y la Música como perfección(el universo entendido como armonía) - Artículo de la Revista MusicalSinfonía Virtual(enlace rotodisponible enInternet Archive;véase elhistorial,laprimera versióny laúltima).
• Sitio web sobre pitagorismo(en inglés).
• Pitágoras y los pitagóricos (I)Pitágoras y los pitagóricos (II)(en español, con multitud de referencias).
• Artículo sobre pitagorismo(en inglés).
• Ausschnitte aus der Biographie aus dem Leben des Pythagoras(en alemán).

• Anónimo:Los versos áureos de Pitágoras(Πυθαγορικὰ χρυσᾶ ἔπη,ca.300 a. C.; enlatín,Carmen aurem):
• Wikisourcecontiene una copia de losVersos dorados de Pitágoras.
  • TextoArchivadoel 5 de octubre de 2011 enWayback Machine.inglés,con otros fragmentos pitagóricos.
    • TextoArchivadoel 15 de noviembre de 2012 enWayback Machine.griegode los Versos Áureos enPDF,con traduccionesitalianas.
    • Texto griegode los Versos Áureos, en elsitiode laBibliotheca Augustana(Augsburgo).

• Hermann Alexander Diels:Fragmentos de lospresocráticos(Die Fragmente der Vorsokratiker). La primera edición se hizo en 1903 en Berlín, y fue dirigida por el propio Diels. A partir de la 5.ª, sustituiría a DielsWalther Kranz.
  • 45:Escuela pitagórica(Pythagoreische Schule).
    • Textogriego: 1.ª ed., de 1903, en facsímil electrónico en Internet Archive.
    • Textogriego de la 2.ª ed., de 1906, con índice electrónico enfrancés,en elsitiode Philippe Remacle (1944 - 2011).

• Anatolio de Laodicea:Sobre ladécada pitagóricay los números que la forman(περὶ δεκάδος καὶ τῶν ἐντὸς αὐτῆς ἀριθμῶν).
  • Texto francés,con introducción en el mismo idioma, en el sitio de Philippe Remacle.

• Espeusipo:fragmento sobre la década pitagórica.
  • Texto francés,con presentación y anotaciones en este idioma, en el mismo sitio: trad. de Paul Tannery (1843 - 1904) publicada en su obraContribución a la historia de la ciencia helena(Pour l’histoire de la science hellène,1887); ed. de 1930, en París.

• Carmen Bonell:La Divina Proporción.
  • Capítulo segundo.

• Datos:Q191359
• Multimedia:Pythagoras/Q191359