Conjunto

Enmatemáticas,unconjuntoes una familia de elementos considerada en sí misma como unobjeto matemático.Los elementos de un conjunto, pueden ser las siguientes:personas,números,colores,letras,figuras,etc. Se dice que unelemento(omiembro) pertenece al conjunto si está definido como incluido de algún modo dentro de él.

Ejemplo: el conjunto de los colores delarcoírises:

AI = {rojo, naranja, amarillo, verde, azul, añil, violeta}

Un conjunto suele definirse mediante una propiedad que todos sus elementos poseen. Por ejemplo, para losnúmeros naturales,si se considera la propiedad de ser unnúmero primo,el conjunto de los números primos es:

P = {2, 3, 5, 7, 11, 13,\dots}

Formalmente, un conjunto es el tipo de objeto matemático del que tratan losaxiomas de Zermelo-Fraenkel.

Historia de conjuntos

El concepto de conjunto como objeto abstracto no comenzó a emplearse en matemáticas hasta el sigloXIX,a medida que se despejaban las dudas sobre la noción deinfinito.^[1] Los trabajos deBernard BolzanoyBernhard Riemannya contenían ideas relacionadas con una visión conjuntista de la matemática. Las contribuciones deRichard Dedekindal álgebra estaban formuladas en términos claramente conjuntistas, que aún prevalecen en la matemática moderna:relaciones de equivalencia,particiones,homomorfismos,etc., y él mismo explicitó las hipótesis y operaciones relativas a conjuntos que necesitó en su trabajo.

Lateoría de conjuntoscomo disciplina independiente se atribuye usualmente aGeorg Cantor.Comenzando con sus investigaciones sobre conjuntos numéricos, desarrolló un estudio sobre los conjuntos infinitos y sus propiedades. La influencia de Dedekind y Cantor empezó a ser determinante a finales del sigloXIX,en el proceso de «axiomatización» de la matemática, en el que todos los objetos matemáticos, como los números, lasfuncionesy las diversasestructuras,fueron construidos con base en los conjuntos.

Definición

[…] entiendo en general por variedad o conjunto toda multiplicidad que puede ser pensada como unidad, esto es, toda colección de elementos determinados que pueden ser unidos en una totalidad mediante una ley.

—Georg Cantor^[2]

Un conjunto es una colección bien definida de objetos,dichos objetos pueden ser cualquier cosa:números,personas, letras, etc. Algunos ejemplos son:

A

es el conjunto de los números naturales menores que 5.

B

es el conjunto de los colores verde, blanco y rojo.

C

es el conjunto de las vocalesa,e,i,oyu.

D

es el conjunto de lospalosde labaraja francesa.

Los conjuntos se denotan habitualmente por letras mayúsculas. Los objetos que componen el conjunto se llamanelementoso miembros. Se dice que «pertenecen» al conjunto y se denota mediante el símbolo∈:^{[n 1]} la expresión $a \in A$ se lee entonces como « $a$ está en $A$ », « $a$ pertenece a $A$ », « $A$ contiene a $a$ », etc. Para la noción contraria se usa el símbolo∉.Por ejemplo:

3 \in A

,

♠ \in D

amarillo \notin B

,

z \notin C

Notación

**Relación de pertenencia.**El conjunto $A$ es un conjunto depolígonos.En la imagen, algunas de las figuras pertenecen a dicho conjunto, pero otras no.

Existen varias maneras de referirse a un conjunto. En el ejemplo anterior, para los conjuntos $A$ y $D$ se usa unadefinición intensivao por comprensión, donde se especifica una propiedad que todos sus elementos poseen. Sin embargo, para los conjuntos $B$ y $C$ se usa unadefinición extensiva,listando todos sus elementos explícitamente.

Es habitual usarllavespara escribir los elementos de un conjunto, de modo que:

B = {verde, blanco, rojo}

C = {a, e, i, o, u}

Esta notación mediante llaves también se utiliza cuando los conjuntos se especifican de forma intensiva mediante una propiedad:

A = {Números naturales menores que 5}

D = {Palos de la baraja francesa}

Otra notación habitual para denotar por comprensión es:

A = {m : m es un número natural, y 1 \leq m \leq 5}

D = {p : p es un palo de la baraja francesa}

F = {n 2 : n es un entero y 1 \leq n \leq 10}

,

En estas expresiones losdos puntos(«:») significan «tal que». Así, el conjunto $F$ es el conjunto de «los números de la forma $n 2$ tal que $n$ es un número entero entre 1 y 10 (ambos inclusive)», o sea, el conjunto de los diez primeroscuadradosdenúmeros naturales.En lugar de los dos puntos se utiliza también labarra vertical(«|») uoblicua«/».

Igualdad de conjuntos

**Conjunto de personas.**El conjunto de «personas» mostrado en la imagen, $A$ ,tiene 8miembros.Este conjunto puede representarse mediantellaveso mediante undiagrama de Venn.El orden de las personas en $A$ es irrelevante.

Un conjunto está totalmente determinado por sus elementos. Por ello, la igualdad de conjuntos se establece como:

Propiedad de laextensionalidad

Dos conjuntos $A$ y $B$ que tengan los mismos elementos son el mismo conjunto, $A = B$ .

Esta propiedad tiene varias consecuencias. Un mismo conjunto puede especificarse de muchas maneras distintas, en particular extensivas o intensivas. Por ejemplo, el conjunto $A$ de los números naturales menores que 5 es el mismo conjunto que $A'$ ,el conjunto de los números 1, 2, 3 y 4. También:

B = {verde, blanco, rojo} = {colores de la bandera de México}

C = {a, e, i, o, u} = {vocales del español}

D = {Palos de la baraja francesa} = {♠, ♣, ♥, ♦}

El orden en el que se precisan los elementos tampoco se tiene en cuenta para comparar dos conjuntos:

B = {verde, blanco, rojo} = {rojo, verde, blanco}

C = {a, e, i, o, u} = {e, i, u, a, o}

Además, un conjunto no puede tener elementos «repetidos», ya que un objeto solo puede o bien ser un elemento de dicho conjunto o no serlo. Se da entonces que, por ejemplo:

{1, 2} = {1, 2, 1}

En ausencia de alguna característica adicional que distinga los «1» repetidos, lo único que puede decirse del conjunto de la derecha es que «1» es uno de sus elementos.

Conjunto vacío

Artículo principal:Conjunto vacío

El conjunto que no contiene ningún elemento se llama el conjunto vacío y se denota por $\emptyset$ o simplemente {}. Algunasteorías axiomáticas de conjuntosaseguran que el conjunto vacío existe incluyendo unaxioma del conjunto vacío.En otras teorías, su existencia puede deducirse. Muchas posibles propiedades de conjuntos son trivialmente válidas para el conjunto vacío.

Propiedades

En lateoría de conjuntos axiomáticaestándar, por elAxioma de extensionalidad,dos conjuntos son iguales si tienen los mismos elementos; por lo tanto solo puede haber un conjunto sin ningún elemento. Por consiguiente, solo hay un único conjunto vacío, y hablamos de "el conjunto vacío"en lugar de"un conjunto vacío".

Para cualquier conjuntoA:

(Veroperaciones con conjuntos)

El conjunto vacío es unsubconjuntodeA:
$\forall A:\emptyset \subseteq A$
La unión deAcon el conjunto vacío esA:
$\forall A:A\cup \emptyset =A$
La intersección deAcon el conjunto vacío es el conjunto vacío:
$\forall A:A\cap \emptyset =\emptyset$
El producto cartesiano de A y el conjunto vacío es el conjunto vacío:
$\forall A:A\times \emptyset =\emptyset$

El conjunto vacío tiene las siguientes propiedades:

Su único subconjunto es el propio conjunto vacío:
$\forall A:A\subseteq \emptyset \Rightarrow A=\emptyset$
El conjunto potencia del conjunto vacío es el conjunto que contiene únicamente el conjunto vacío:
$2^{\emptyset }=\{\emptyset \}$
Su número de elementos (cardinalidad) es cero:
$\mathrm {n} (\emptyset )=0$

(La lista de símbolos matemáticos empleados se encuentraaquí).

Subconjuntos

Artículo principal:Subconjunto

**Subconjunto.** $B$ es unsubconjuntode $A$ (en particular unsubconjunto propio).

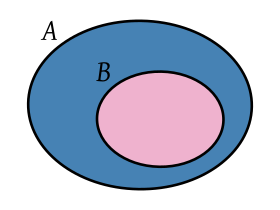
Un subconjunto $A$ de un conjunto $B$ ,es un conjunto que contiene algunos de los elementos de $B$ (o quizá todos):

Un conjunto $A$ es unsubconjuntodel conjunto $B$ si cada elemento de $A$ es a su vez un elemento de $B$ .

Cuando $A$ es un subconjunto de $B$ ,se denota como $A \subseteq B$ y se dice que « $A$ está contenido en $B$ ». También puede escribirse $B \supseteq A$ ,y decirse que $B$ es unsuperconjuntode $A$ y también « $B$ contiene a $A$ » o « $B$ incluye a $A$ ».

Todo conjunto $A$ es un subconjunto de sí mismo, ya que siempre se cumple que «cada elemento de $A$ es a su vez un elemento de $A$ ». Es habitual establecer una distinción más fina mediante el concepto desubconjunto propio: $A$ es un subconjunto propio de $B$ si es un subconjunto de $B$ pero no es igual a $B$ .Se denota como $A ⊊ B$ ,es decir: $A \subseteq B$ pero $A \neq B$ (y equivalentemente, para un superconjunto propio, $B ⊋ A$ ).^{[n 2]}

Ejemplos.

El «conjunto de todos los hombres» es un subconjunto propio del «conjunto de todas las personas».

{1, 3} ⊊ {1, 2, 3, 4

}

{1, 2, 3, 4} \subseteq {1, 2, 3, 4

}

Conjuntos disjuntos

Artículo principal:Conjuntos disjuntos

Dos conjuntos $A$ y $B$ son disjuntos si no tienen ningún elemento en común. Por ejemplo, los conjuntos de losnúmeros racionalesy losnúmeros irracionalesson disjuntos: no hay ningún número que sea a la vez racional e irracional. Laintersecciónde dos conjuntos disjuntos es el conjunto vacío.

Cardinalidad

Artículo principal:Número cardinal

Los conjuntos pueden serfinitosoinfinitos.En el caso de un conjunto finito se pueden contar los elementos del conjunto:

El número de elementos de un conjunto finito es sucardinal.

El cardinal se denota por $| A |$ , $card(A)$ o $#A$ .Así, en los ejemplosanteriores,se tiene que $| A | = 4$ (cuatro números), $| B | = 3$ (tres colores) y $| F | = 10$ (diez cuadrados). El único conjunto cuyo cardinal es 0 es elconjunto vacío $\emptyset$ .

Existen, a su vez, determinadaspropiedades de cardinalidad.Si tomamos como ejemplo dos conjuntos,AyB:

$n(\emptyset )=0$
$A=B\Rightarrow n(A)=n(B)$
$A\subseteq B\Rightarrow n(A)\leq n(B)$
$n(A\cup B)=n(A)+n(B)-n(A\cap B)$
$n(U)=n(A)+n(A^{c})$
$n(A-B)=n(A)-n(A\cap B)$

Y en el caso de tres conjuntos,A,ByC:

$n(A\cup B\cup C)=n(A)+n(B)+n(C)-n(A\cap B)-n(A\cap C)-n(B\cap C)+n(A\cap B\cap C)$
$n(A-(B\cup C))=n(A)-n(A\cap B)-n(A\cap C)+n(A\cap B\cap C)$
$n((A\cap B)-C)=n(A\cap B)-n(A\cap B\cap C)$
$n((A\cup B)-C)=n(A\cup B)-n(A\cap C)-n(B\cap C)+n(A\cap B\cap C)$

En un conjunto infinito no hay un número finito de elementos. Es el caso por ejemplo de losnúmeros naturales: $N = {1, 2, 3,\dots}$ .Sin embargo, existe una manera de comparar conjuntos infinitos entre sí, y se obtiene que existen conjuntos infinitos «más grandes» que otros. El «número de elementos» de un conjunto infinito es unnúmero transfinito.

Cardinalidad de los reales

Artículo principal:Número real

Uno de los resultados más importantes deGeorg Cantorfue que la cardinalidad de los reales ( ${\mathfrak {c}}$ ) es más grande que la de los números naturales ( $\aleph _{0}$ ). Esto es, que hay más números realesRque números enterosN.Concretamente, Cantor mostró que ${\mathfrak {c}}=2^{\aleph _{0}}>{\aleph _{0}}\,$ .

La hipótesis del continuo afirma que no existen conjuntos con cardinalidades intermedias entre losnaturalesy losreales:

No existe ningún conjunto $A$ tal que su cardinal $| A |$ cumpla:

\aleph _{0}<|A|<2^{\aleph _{0}}.

Si se asume elaxioma de elección,la estructura de los cardinales infinitos es más clara: todos los cardinales infinitos sonálefsy estánbien ordenados,por lo que existe solo un cardinal inmediatamente superior a $ℵ 0$ ,denotado por $ℵ 1$ .La hipótesis es equivalente entonces a:

El cardinal del conjunto de los números reales es el inmediatamente superior al cardinal de los números naturales:

2^{\aleph _{0}}=\aleph _{1}.

Operaciones con conjuntos

Unión

Intersección

Diferencia

Complemento

Diferencia simétrica

Artículo principal:Álgebra de conjuntos

Existen varias operaciones básicas que pueden realizarse, partiendo de ciertos conjuntos dados, para obtener nuevos conjuntos:

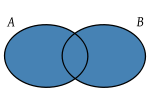
Unión:(símbolo $\cup$ ) Launiónde dos conjuntos $A$ y $B$ ,que se representa como $A \cup B$ ,es el conjunto de todos los elementos que pertenecen al menos a uno de los conjuntos $A$ y $B$ .
$A\cup B=\{x\mid x\in A\lor x\in B\}$
Intersección:(símbolo $\cap$ ) Laintersecciónde dos conjuntos $A$ y $B$ es el conjunto $A \cap B$ de los elementos comunes aAyB.
$A\cap B=\{x\mid x\in A\land x\in B\}$
Diferencia:(símbolo \) Ladiferenciadel conjunto $A$ con $B$ es el conjunto $A\B$ que resulta de eliminar de $A$ cualquier elemento que esté en $B$ .
$A\setminus B=\{x\mid x\in A\land x\notin B\}$
Complemento:Elcomplementode un conjunto $A$ es el conjunto $A ∁$ que contiene todos los elementos que no pertenecen a $A$ ,respecto a unconjunto $U$ que lo contiene.
$A^{c}=\{x\in U\mid x\not \in A\}$
Diferencia simétrica:(símbolo Δ) Ladiferencia simétricade dos conjuntos $A$ y $B$ es el conjunto $A Δ B$ con todos los elementos que pertenecen, o bien a $A$ ,o bien a $B$ ,pero no a ambos a la vez.
$A\bigtriangleup B=\{x\mid x\in A\setminus B\lor x\in B\setminus A}\$
Producto cartesiano:(símbolo ×) Elproducto cartesianode dos conjuntos $A$ y $B$ es el conjunto $A \times B$ de todos lospares ordenados $(a, b)$ formados con un primer elemento $a$ perteneciente a $A$ ,y un segundo elemento $b$ perteneciente a $B$ .

Ejemplos

${1, a,0} \cup {2, b} = {2, b,1, a,0}$
${5, z,♠} \cap {♠, a} = {♠}$
${5,z,♠} \ {♠,a} = {5,z}$
${♠, 5} Δ {8, #, ♠} = {5, #, 8}$
${1, a,0} \times {2, b} = {(1, 2), (1, b), (a,2), (a, b), (0, 2), (0, b)}$

Véase también

Notas

↑Este símbolo lo introdujo Peano. Vid Matemática Moderna de André Warusfel sobre epsilon y Nachbin en su Álgebra Elemental (pág. 1 y pág. 2) habla de: "La notación de Peano x∈X ".
↑También se utiliza la notación $A \subset B$ y $B \supset A$ ,pero según el autor esto puede denotar subconjunto, $A \subseteq B$ y $B \supseteq A$ ;o subconjunto propio, $A ⊊ B$ y $B ⊋ A$ .VéaseSubconjunto.

Referencias

↑Esta sección está basada enFerreirós, J.«The early development of set theory».En Edward N. Zalta, ed.The Stanford Encyclopedia of Philosophy(Fall 2011 edition)(en inglés).Archivado desdeel originalel 30 de julio de 2012.Consultado el 15 de diciembre de 2011.
↑VéaseCantor, Georg(2006) [1872-1899].Fundamentos para una teoría general de conjuntos. Escritos y correspondencia selecta.Edición de José Ferreirós. Crítica. p. 137.ISBN 84-8432-695-0.

Bibliografía

Courant, Richard; Robbins, Herbert; Stewart, Ian (1996).What is Mathematics? An Elementary Approach to Ideas and Methods(en inglés).Oxford University Press.ISBN 0-19-510519-2.Suplemento del capítulo II.
Ivorra, Carlos,Lógica y teoría de conjuntos,consultado el 18 de abril de 2011..
Jech, Thomas.«Set Theory».En Edward N. Zalta, ed.The Stanford Encyclopedia of Philosophy(Spring 2009 Edition)(en inglés).Consultado el 22 de abril de 2011.
Lipschutz, Seymour (1991).Teoría de conjuntos y temas afines.McGraw-Hill.ISBN 968-422-926-7.
Nachbin, Leopoldo: Álgebra elemental (1986) Rochester, Nueva York; editora: Eva V. Chesnau. Edición de la OEA, traducida al español por César E. Silva.

Bibliografía adicional

Halmos, Paul R.:Teoría intuitiva de conjuntos(1965) Compañía editorial Continental S.A. México 22, D.F. primera edición en español.

Enlaces externos

Wikimedia Commonsalberga una categoría multimedia sobreConjuntos.
Weisstein, Eric W.«Set».En Weisstein, Eric W, ed.MathWorld(en inglés).Wolfram Research.
Esta obra contiene una traducción derivada de «Set» de Wikipedia en inglés, publicada porsus editoresbajo laLicencia de documentación libre de GNUy laLicencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.

Datos:Q36161
Multimedia:Sets (mathematics)/Q36161

[3] Este símbolo lo introdujo Peano. Vid Matemática Moderna de André Warusfel sobre epsilon y Nachbin en su Álgebra Elemental (pág. 1 y pág. 2) habla de: "La notación de Peano x∈X ".

[4] También se utiliza la notación $A \subset B$ y $B \supset A$ ,pero según el autor esto puede denotar subconjunto, $A \subseteq B$ y $B \supseteq A$ ;o subconjunto propio, $A ⊊ B$ y $B ⊋ A$ .VéaseSubconjunto.

[1] Esta sección está basada enFerreirós, J.«The early development of set theory».En Edward N. Zalta, ed.The Stanford Encyclopedia of Philosophy(Fall 2011 edition)(en inglés).Archivado desdeel originalel 30 de julio de 2012.Consultado el 15 de diciembre de 2011.

[2] VéaseCantor, Georg(2006) [1872-1899].Fundamentos para una teoría general de conjuntos. Escritos y correspondencia selecta.Edición de José Ferreirós. Crítica. p. 137.ISBN 84-8432-695-0.

[1]

[2]

[n 1]

[n 2]