Dodecágono

Dodecagono
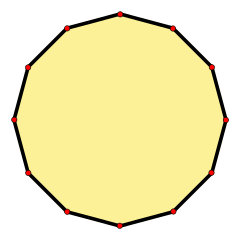	; Un dodecágono regular
Características
Tipo	Polígono regular
Lados	12
Vértices	12
Grupo de simetría	,orden 2x12
Símbolo de Schläfli	{12}, t{6} (dodecágono regular)
Diagrama de Coxeter-Dynkin	;
Polígono dual	Autodual
Área	; (lado)
Ángulo interior	150°
Propiedades
	Convexo,isogonal,cíclico
	[editar datos en Wikidata]

Undodecágono,en lageometría,es unpolígonode12 ladosy 12vértices.Si al prolongar un lado, toda la figura queda exactamente en uno de los semiplanos determinados por el lado y sus prolongaciones, el polígono esconvexo.En el caso de que exista un lado con sus prolongaciones tal que la figura se sitúe en los dos semiplanos definidos por tal lado y sus prolongaciones, el polígono escóncavo.

La suma de susángulos interioreses de 1800°.

Propiedades

Un dodecágono tiene 54diagonales,resultado que se puede obtener aplicando la ecuación general para determinar el número de diagonales de un polígono, $D=n(n-3)/2$ ;siendo el número de lados $n=12$ ,se tiene que:

D={\frac {12(12-3)}{2}}=54

La suma de todos losángulos internosde cualquier dodecágono es 1800gradoso $10\pi$ radianes.
El ángulo central de un dodecágono regular es de 30°.

El número de puntos en que se intersecan las diagonales de un dodecágono regular es 495.

Dodecágono regular

Undodecágono regulares un dodecágono con igual longitud en todos sus lados y cuyosángulos internostienen todosla misma medida:150° o $5\pi /6$ rad. Cadaángulo externodel dodecágono regular mide 30° o $\pi /6$ rad.

Un dodecágono regular tienesímbolo de Schläfli{12} y puede ser construido como un hexágono truncado, t{6}, o un triángulo doblemente truncado, tt{3}.

Perímetro

Elperímetrode un dodecágono regular de lado $t$ es

P=12\cdot t

O bien, en términos del circunradio $r$ es^[1]

{\begin{aligned}P&=24r\tan \left({\frac {\pi }{12}}\right)=12r{\sqrt {2-{\sqrt {3}}}}\\&\simeq 6.21165708246\,r\end{aligned}}

Área

Eláreade un dodecágono regular de lado $t$ es^[2]

A={\frac {3\cdot t^{2}}{\tan({\frac {\pi }{12}})}}=t^{2}\cdot (6+3{\sqrt {3}})\simeq 11,1962\ t^{2}

donde $\pi$ es la constantepiy $\tan$ es la funcióntangentecalculada en radianes.

O bien, en función de laapotema $a$ y del lado $t$ del dodecágono,

A={\frac {P\cdot a}{2}}={\frac {12\cdot t\cdot a}{2}}=6\cdot t\cdot a

También, en función de únicamente la apotema $a$ ,^[2]

A=a^{2}\cdot (24-12{\sqrt {3}})

Y, finalmente, en función del radio $r$ delcircunferencia circunscritaal dodecágono,^[3]

A=3r^{2}

Su área representa los ${\frac {2}{\sqrt {3}}}$ del área del hexágono regular inscrito en la misma circunferencia.

Construcción de dodecágono

Como 12=2²×3, el dodecágono regular esconstruibleusandoregla y compás:

Construcción de un dodecágono regular en unacircunferencia circunscritadada

Construcción de un dodecágono regular
a partir de una longitud de lado dada, animación. (La construcción es muy similar a la deloctógono)

Disección

Hipercubo	Disección en 15 rombos	Disección en 60 rombos

Harold Scott MacDonald Coxeterestableció que cadazonágono(un 2m-gono cuyos lados opuestos son paralelos y de igual longitud) se puede diseccionar enm(m-1)/2 paralelogramos.^[4]

En particular, esto es cierto para polígonos regulares con muchos lados, en cuyo caso los paralelogramos son todos rombos. Para eldodecágono regular,m=6, se puede dividir en 15 figuras: 3 cuadrados, 6 rombos anchos de 30° y 6 rombos estrechos de 15°. Esta descomposición se basa en una proyección según elpolígono de Petriede unhexeracto,con 15 de sus 240 caras. La secuencia OEIS (sucesiónA006245enOEIS) define el número de soluciones como 908, incluidas rotaciones de hasta 12 veces y formas quirales en reflexión.

Disección en 15 rombos
hexeracto

Una de las formas en que se utilizan es comobloques patrónenmatemática manipulativa,creando distintos dodecágonos diferentes a partir de otras figuras.^[5] Están relacionados con las disecciones rómbicas, con 3 rombos de 60° fusionados en hexágonos, trapecios de medio hexágono o divididos en 2 triángulos equiláteros.

Otras disecciones
Regular		Bloques patrón

Simetría

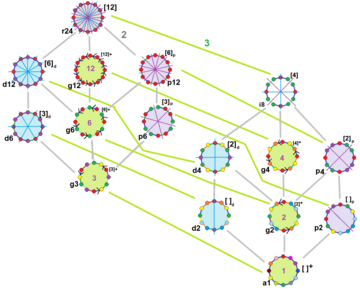
El dodecágono regular poseesimetría diedralDih₁₂de orden 24. Incluye 15 subgrupos distintos de simetrías diedrales y cíclicas.

John Conwayclasificó estas simetrías usando una letra y el orden de la simetría a continuación. Asignó la letraral grupo de simetría de la figura regular; y en el caso de los subgrupos utilizó la letrad(de diagonal) para las figuras con ejes de simetría solo a través de sus vértices;ppara figuras con ejes de simetría solo a través de ejes perpendiculares a sus lados;ipara figuras con ejes de simetría tanto a través de vértices como a través de centros de lados; ygpara aquellas figuras solo con simetría rotacional. Cona1se etiquetan aquellas figuras con ausencia de simetría. Los tipos de simetrías más bajos permiten disponer de uno o más grados de libertad para definir distintas figuras irregulares.^[6] Solo el subgrupog12no tiene grados de libertad, pero puede verse como ungrafo dirigido.(Véase un ejemplo en laTeoría de grupos de John Conway)

Ejemplos de dodecágonos según su simetría
r24
d12	g12	p12	i8
d6	g6	p6	d4	g4	p4
g3			d2	g2	p2
a1

Teselados

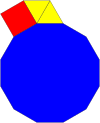
Una combinación de dodecágonos regulares con otros polígonos regulares puederellenar el planode 4 formas:

3.12.12	4.6.12	3.3.4.12	3.4.3.12

Se muestran 3 ejemplos deteselados regularesque utilizan dodecágonos regulares, definidos por suconfiguración de vértices:

1-uniforme		2-uniforme
3.12.12	4.6.12 4.6.12	3.12.12; 3.4.3.12

Dodecágono alabeado

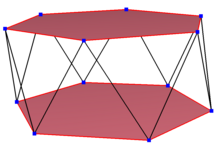
Undodecágono alabeadoes unpolígono alabeadocon 12 vértices y aristas, pero que no están situadas en el mismo plano. El interior de tal dodecágono no está generalmente definido. Un "dodecágono en zig-zag alabeado" tiene vértices que se alternan entre dos planos paralelos.

Unpolígono alabeadoes unafigura isogonalcon longitudes de arista iguales. En 3 dimensiones será un dodecágono alabeado en zig-zag y se puede ver en los vértices y aristas laterales de unantiprisma hexagonalcon la misma simetría D_5d,[2⁺,10], de orden 20. Elantiprisma dodecagrámico,s {2,24/5} yantiprisma cruzado dodecagrámico,s{2,24/7} también incluyen dodecágonos alabeados regulares.

Polígonos de Petrie

El dodecágono regular es elpolígono de Petriepara muchos politopos de dimensiones superiores, visto comoproyeccionessobre elplano de Coxeter.Ejemplos en 4 dimensiones son elicositetracoron,el24-cell snub,el6-6 duoprismay la6-6 duopirámide.En 6 dimensiones, elhexeracto,el6-ortoplex,el2₂₁,y el1₂₂.También es el polígono de Petrie para elgran 120-celly para elgran 120-cell estrellado.

Dodecágonos alabeados regulares en dimensiones más altas
E₆		F₄		2G₂(4D)
2₂₁	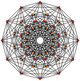1₂₂	icositetracoron	24-cell snub	6-6 duopirámide	6-6 duoprisma
A₁₁	D₇		B₆
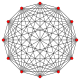símplex	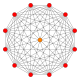(4₁₁)	1₄₁	6-ortoplex	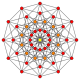hexeracto

Figuras relacionadas

Undodecagramaes un polígono en estrella de 12 lados, representado por el símbolo {12/n}. Existe unaestrellaregular: {12/5}, que usa los mismos vértices, pero conecta cada quinto punto. También hay tres compuestos: {12/2} se reduce a 2{6} como doshexágonos,y {12/3} se reduce a 3{4} como trescuadrados,{12/4} se reduce a 4 {3} como cuatro triángulos, y {12/6} se reduce a 6{2} como seisdígonosdegenerados.

Estrellas y compuestos
n	1	2	3	4	5	6
Forma	Polígono	Compuestos			Polígono de estrella	Compuesto
Imagen	{12/1} = {12}	{12/2} or 2{6}	{12/3} or 3{4}	{12/4} or 4{3}	{12/5}	{12/6} or 6{2}

Los truncamientos más profundos del dodecágono regular y los dodecagramas pueden producir formas poligonales de estrellas intermedias isogonales (figura isogonal) con vértices espaciados iguales y dos longitudes de borde. Un hexágono truncado es un dodecágono, t{6} = {12}. Un hexágono cuasitruncado, invertido como {6/5}, es un dodecagrama: t{6/5} = {12/5}.^[7]

Truncamientos de vértice del hexágono transitivos
Cuasirregular	Isogonal		Cuasirregular
t{6}={12}			t{6/5}={12/5}

Ejemplos

En una tipografía recta, las letras mayúsculasE,HyX(eIen algunas fuentes depalo seco) tienen contornos dodecagonales. Unacruzformada por dos rectángulos cruzados es un dodecágono, al igual que el logotipo de la división de automóvilesChevrolet.

El dodecágono regular ocupa un lugar destacado en muchos edificios. LaTorre del Oroes unaatalayamilitar dodecagonal situada enSevilla,al sur deEspaña,construida durante la época delimperio almohade.Laiglesia de la Vera Cruzde principios del sigloXIIIenSegovia,también en España, es dodecagonal. Otro ejemplo es la Porta di Venere (Puerta de Venus), enSpello,Italia.Construida en el sigloIa. C., posee dos torres dodecagonales, llamadas "Torres de Propercio".

Entre lasmonedas dodecagonalesregulares, se incluyen:

Tres peniques,desde 1937 hasta 1971, cuando dejó de ser moneda de curso legal.
Moneda británica de una libra,introducida en 2017.
Moneda de 50 centavos australiana
50 centavos de Fiyi
50-seniti de Tonga,desde 1974
50 centavos de las Islas Salomón
25 kuna de Croacia
500 lei de Rumanía,2001-2005
Penique de Canadá,1982-1996
20 đồng de Vietnam del Sur,1968-1975
50 ngwee de Zambia,1969-1992
50 tambala de Malaui,1986-1995
20 centavos de México,1992-2009

Véase también

Número dodecagonal
Dodecaedro,unpoliedroarquimediano con 12 caraspentagonales
Dodecagrama

Referencias

↑Clarence Addison Willis (1922). B. Blakiston's Son & Company, ed.Plane Geometry: Experiment, Classification, Discovery, Application(en inglés).
↑^a ^bSapiña, R.«Calculadora del área y perímetro del dodecágono regular».Problemas y ecuaciones.ISSN 2659-9899.Consultado el 3 de julio de 2020.
↑Wells, David (1997).«The Penguin Dictionary of Curious and Interesting Numbers».Penguin(en inglés):137.ISBN 0140261494.
↑Harold Scott MacDonald Coxeter,Mathematical recreations and Essays, Thirteenth edition, p.141
↑"Doin' Da' Dodeca'" onmathforum.org
↑John H. Conway, Heidi Burgiel,Chaim Goodman-Strauss,(2008) The Symmetries of Things,ISBN 978-1-56881-220-5(Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
↑The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994),Metamorphoses of polygons,Branko Grünbaum

Enlaces externos

Wikimedia Commonsalberga una categoría multimedia sobredodecágonos.
Wikcionariotiene definiciones y otra información sobredodecágono.
Weisstein, Eric W.«Dodecagon».En Weisstein, Eric W, ed.MathWorld(en inglés).Wolfram Research.
Kürschak's Tile and Theorem
Definition and properties of a dodecagonWith interactive animation
The regular dodecagon in the classroom,usingpattern blocks

Véase también

Datos:Q212074
Multimedia:12-gons/Q212074

[CAW-1] Clarence Addison Willis (1922). B. Blakiston's Son & Company, ed.Plane Geometry: Experiment, Classification, Discovery, Application(en inglés).

[pye-2] Sapiña, R.«Calculadora del área y perímetro del dodecágono regular».Problemas y ecuaciones.ISSN 2659-9899.Consultado el 3 de julio de 2020.

[wm-3] Wells, David (1997).«The Penguin Dictionary of Curious and Interesting Numbers».Penguin(en inglés):137.ISBN 0140261494.

[4] Harold Scott MacDonald Coxeter,Mathematical recreations and Essays, Thirteenth edition, p.141

[5] "Doin' Da' Dodeca'" onmathforum.org

[6] John H. Conway, Heidi Burgiel,Chaim Goodman-Strauss,(2008) The Symmetries of Things,ISBN 978-1-56881-220-5(Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)

[7] The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994),Metamorphoses of polygons,Branko Grünbaum

[1]

[2]

[3]

[4]

[5]

[6]

[7]