Fibrado

Entopología,unfibrado(ohaz fibrado) es unafunción continua suprayectivaπ, de unespacio topológicoEen otroespacio topológicoB,satisfaciendo otra condición que lo hace de una forma particularmente simple localmente. Introduciendo otro espacio topológico F, utilizamos la función de proyección deB×F→Bcomo modelo. Por ejemplo en el caso de unfibrado vectorial,Fes unespacio vectorial.

Definición

Unfibradoconsiste en una cuaterna $(E,B,\pi,F)\,$ ,donde $E\,$ , $B\,$ y $F\,$ son espacios topológicos y $\pi:E\longrightarrow B$ es unaaplicación continuaysobreyectiva,de manera que para cualquier $x\in B\,$ existe un entorno $U\,$ de $x$ en $B\,$ ,y un homeomorfismo $\phi:\pi ^{-1}(U)\longrightarrow U\times F\,$ tal que $\pi ={\mbox{proj}}_{1}\circ \phi \,$ ,con ${\mbox{proj}}_{1}:U\times F\longrightarrow U$ , ${\mbox{proj}}_{1}(x,y)=x\,$ .Equivalentemente, para todo punto de B existe un entorno $U$ y un homeomorfismo $\phi$ tal que el siguiente diagrama conmuta:

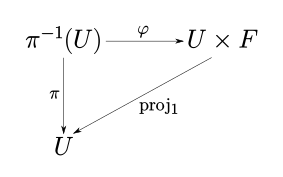
La aplicación $\pi$ es abierta por ser una proyección en un producto cartesiano yBtiene la topología cociente. El espacio $B\,$ se llama elespacio de basedel fibrado, $E\,$ elespacio total,para cualquier $x\in B\,$ , $\pi ^{-1}(x)\,$ se llama la fibra en $x\,$ y la función ${\mbox{proj}}_{1}\,$ se llama la proyección. Se denota $E|_{U}=\pi ^{-1}(U)$ y se dice que $\pi$ eslocalmente trivialy el par $(U,\phi )$ es unatrivialización local.Es habitual escribir $E$ en vez de $(E,B,\pi,F)$ si $B,\pi$ y $F$ se pueden entender por contexto y decir queEes unfibrado sobre B.

Ejemplos

El primer ejemplo es elfibrado productoofibrado trivialdado por $(B\times F,B,{\mbox{proj}}_{1},F)$ .

Un ejemplo de fibrado no (globalmente) trivial es laBanda de Möbiuscomo espacio totalE,base $B\cong S^{1}$ un círculo y fibraF=(0,1)un segmento de línea. La rotación de los segmentosFa lo largo de la cinta es apreciable sólo globalmente ya que localmente la estructura de la banda es homeomorfa a un producto $U\times (0,1)$ .Una descripción analítica explícita es

$E={\frac {\{(x,y)\in \mathbb {R} \times (0,1)\}}{(x,y)\sim (x+1,1-y)}},\quad B\cong S^{1}={\frac {x\in \mathbb {R} }{x\sim x+1}}$

y la aplicación $\pi$ es la proyección en la primera coordenada.

Unfibrado vectorial $(E,B,\pi,F)$ es en particular un fibrado. El fibrado vectorial se llamarealocomplejosi la fibraFes un espacio vectorial real o complejo respectivamente. Elfibrado tangentey el fibrado cotangente son ejemplos de fibrados vectoriales.

Unespacio recubridorocubiertaes un fibrado, aquí laFes un conjunto discreto.

Existen en la literatura una amplia cantidad de ejemplos con variedades específicas o fibras prescritas. Un par de ejemplos recurrentes en topología algebraica son la fibración de Hopf de $S^{2n+1}$ sobre $\mathbb {C} \mathbb {P} ^{n}$ con fibra $S^{1}$ y la fibración delespacio de caminosde un espacio topológico con punto base $(X,x_{0})$ , ${\mathcal {P}}(X)\longrightarrow X$ con fibra isomorfa al espacio de lazos $\Omega (X)$ de $X$ .

Morfismos

Unmorfismoentre dos fibrados $(E',B',\pi ',F')$ y $(E,B,\pi,F)$ consiste en un par de aplicaciones continuas $(f,{\widetilde {f}})$ , $f:B'\longrightarrow B$ y ${\widetilde {f}}:E'\longrightarrow E$ ,tales que ${\widetilde {f}}\circ \pi =\pi 'f$ .Nótese que la aplicación ${\widetilde {f}}$ determina la aplicación $f$ .Para cada punto $x'\in B'$ se induce una aplicación ${\widetilde {f}}_{x}:E'_{x'}\longrightarrow E_{f(x')}$ .

Los morfismos entre fibrados se puede componer mediante $(f,{\widetilde {f}})\circ (g,{\widetilde {g}}):=(f\circ g,{\widetilde {f}}\circ {\widetilde {f}})$ .En particular tenemos la noción deisomorfismode fibrados: un morfismo $(f,{\widetilde {f}})$ entre dos fibrados $(E',B',\pi ',F')$ y $(E,B,\pi,F)$ es unisomorfismosi existe un morfismo $(g,{\widetilde {g}})$ entre $(E,B,\pi,F)$ y $(E',B',\pi ',F')$ tal que $f\circ g=Id_{B},g\circ f=Id_{B'}$ y ${\widetilde {f}}\circ {\widetilde {g}}=Id_{E},{\widetilde {g}}\circ {\widetilde {f}}=Id_{E'}$ .Observemos que una condición necesaria para que los fibrados sean isomorfos es que las fibras sean isomorfas.

Unmorfismo verticalen un fibrado $(E,B,\pi,F)$ es un morfismo $(f,{\widetilde {f}})$ con $f=Id_{B}$ .Un primer paso en la clasificación de fibrados es fijar el espacio baseBy clasificar los fibrados con baseBsalvo isomorfismo.

Operaciones

En esta sección introducimos posibles operaciones en la categoría de fibrados en espacios topológicos. Para fibrados particulares es posible desarrollar operaciones específicas, por ejemplo las operaciones de álgebra lineal como elespacio dual,eldeterminante,elproducto tensorialy elproducto exteriorextienden a las correspondientes nociones para fibrados vectoriales. Las operaciones aquí descritas son generales.

Elpull-backde fibrados es una de las operaciones decambio de base.Sea $(E,B,\pi,F)$ un fibrado y $f:B'\longrightarrow B$ una aplicación continua. El fibradopull-backdeEa través deftiene por espacio total

$f^{*}E:=\{(x',e)\in B'\times E|f(x)=\pi (e)\}$

con aplicación proyección $\pi ':f^{*}E\longrightarrow B'$ , $\pi '(x',e)=x'$ .Entonces es sencillo demostrar que $(f^{*}E,B',\pi ',F)$ es un fibrado. Nótese que las fibras de $E$ y $f^{*}E$ son isomorfas y que existe un morfismo natural de $f^{*}E$ y $E$ . Esta operación es functorial contravariante con respecto a la composición de morfismos, es decir, $f^{*}(g^{*}E)=(g\circ f)^{*}E$ y $id^{*}E=E$ .El fibradopull-backdepende en general deEy de la aplicaciónfpero siEes un fibrado trivial $f^{*}E$ también.

Larestricciónde fibrados. Sea $A\subset B$ un subespacio, $i:A\longrightarrow B$ la inclusión yEun fibrado sobreB.El fibradorestricciónde E al subespacio A es el fibrado $i^{*}E$ .

Elproducto(cartesiano) de dos fibrados $(E,B,\pi,F)$ y $(E',B',\pi ',F')$ es el fibrado $(E\times E',B\times B',\pi \times \pi ',F\times F')$ .

Si E y E' son fibrados sobre la misma baseB,elproducto fibrado sobre Bse define como

$E\times _{B}E':=\{(e,e')\in E\times E'|\pi (e)=\pi '(e')\}\longrightarrow B.$

Las fibras son por tanto isomorfas a $F\times F'$ .Nótese que el fibrado $E\times _{B}E'$ no es más que la restricción del fibrado producto cartesiano a la diagonal $\Delta _{B}\subset B\times B$ con la identificación $\Delta _{B}\cong B$ .

Propiedades homotópicas

En esta sección se mencionan propiedades de los fibrados en relación con las homotopías. Las demostraciones son ejercicios y se pueden encontrar en cualquier texto de referencia.

El resultado fundamental para entender el comportamiento de los fibrados por homotopía es el siguiente: Sea $E\longrightarrow B\times [0,1]$ un fibrado y $\pi _{1}:B\times [0,1]\longrightarrow B$ la proyección al primer factor, entonces $E\cong \pi _{1}^{*}\left(E|_{B\times \{0\}}\right)$ .En particular $E|_{B\times \{t\}}\cong \left(E|_{B\times \{0\}}\times [0,1]\right)|_{B\times \{t\}}\cong E|_{B\times \{0\}}\times \{t\}\cong E|_{B\times \{0\}}$ .

Del enunciado anterior se siguen dos corolarios:

(1) Sean $f\simeq g:B'\longrightarrow B$ aplicaciones continuas y homotópicas y E un fibrado sobre B. Entonces $f^{*}E\cong g^{*}E.$

(2) Sea $r:B\longrightarrow A\subset B$ un retracto de deformación y E un fibrado sobre B. Entonces, $E|_{B}\cong r^{*}(E|_{A}).$

Se deduce del segundo resultado que si el espacio base B es contráctil cualquier fibrado $(E,B,\pi,F)$ es isomorfo al fibrado trivial $E\cong B\times F$ .

Secciones

Unasecciónde un fibrado es una función continua,f:B→Etal queπ(f(x))=x,paraxenB.En general un fibrado no tiene secciones, uno de los propósitos de la teoría es explicar la existencia de estas así como su cuantificación. Nótese que los fibrados vectoriales siempre tienen una sección, lasección cero.

Laobstruccióna la existencia de una sección se puede codificar en elementos de una teoría de cohomología de la base; en el caso de que el espacio base sea unCW-complejo, hallar obstrucciones en la cohomología celular conduce a la teoría de lasclases característicasentopología algebraica.Una aplicación sencilla de esta teoría es demostrar que las esferas de dimensión par no tienen campos tangentes no nulos, luego no son paralelizables.

Grupo estructural

Existe, a veces, ungrupo topológicoGde transformaciones deE,tal que siρdenota la acción,π(ρ(g)[e])= π(e)paragenGyeenE.La condición indica que cadaG-órbitareside dentro de una sola fibra. En ese caso,Gse llamagrupoestructural del fibrado. Para calificar comoG-fibrado, las condiciones que emparejan entre las vecindades trivializable locales tendrían que serlos intertwinersdeG-accionestambién.

Si, además, actúaGlibremente,transitivamenteycontinuamentesobre cada fibra, entonces llamamos al fibradofibrado principal.Un ejemplo de un fibrado principal que ocurre naturalmente en geometría es el fibrado de todas las bases de losespacios tangentesa unavariedad,conGgrupo general lineal;la restricción engeometría de Riemanna las bases ortonormales, limitaría G algrupo ortogonal.Veavierbeinpara más detalles.

HacerGexplícito es esencial para las operaciones de crear unfibrado asociado,y hacer precisa lareducción del grupo estructural de un fibrado.

Aplicaciones

El lenguaje de la teoría de fibrados permite la expresión de situaciones físicas en términos matemáticos. Una instancia de ello son lasteorías gaugedonde los fibrados principales codifican las nociones físicas de simetrías, potenciales y fuerza en términos del grupo de estructura, lasconexionesy lacurvatura.

Referencias

Steenrod, Norman(1951),The Topology of Fibre Bundles,Princeton University Press,ISBN 0-691-00548-6..
Bleecker, David (1981),Gauge Theory and Variational Principles,Reading, Mass: Addison-Wesley publishing,ISBN 0-201-10096-7..
Ehresmann, C.«Les connexions infinitésimales dans un espace fibré différentiable».Colloque de Topologie (Espaces fibrés), Bruxelles, 1950.Georges Thone, Liège; Masson et Cie., Paris, 1951. pp. 29-55.
Husemöller, Dale(1994),Fibre Bundles,Springer Verlag,ISBN 0-387-94087-1.
Michor, Peter W. (2008),Topics in Differential Geometry,Graduate Studies in Mathematics,Vol. 93, Providence: American Mathematical Society.(to appear).
Voitsekhovskii, M.I. (2001),«Fibre_space&oldid=18348»,en Hazewinkel, Michiel, ed.,Encyclopaedia of Mathematics(en inglés),Springer,ISBN 978-1556080104.

Véase también

Enlaces externos

PlanetMath: Fiber Bundle
Weisstein, Eric W.«Fiber Bundle».En Weisstein, Eric W, ed.MathWorld(en inglés).Wolfram Research.

Datos:Q1154996