Vector

Representación gráfica de un vector como unsegmentoorientado sobre unarecta.

Enmatemáticayfísica,unvector​ es cualquier tema matemático que se puede representar mediante unsegmentoderectaorientadodentro delespacio euclidiano.

Un vector con un origen fijado queda determinado a partir de dos elementos:

• Unasemirrectaa partir de dicho origen, es decir, unadirecciónhacia la que apunta.​
• Un número no negativo, llamadomódulodel vector y que mide su tamaño.

Alternativamente, se puede fijar unsistema de coordenadasdel espacio$n$-dimensional; entonces un vector queda unívocamente determinado mediante$n$números, llamadoscoordenadasdel vector. El ejemplo más sencillo son lascoordenadas cartesianas,un sistema de$n$ejes reglados que se suelen tomarperpendicularesentre sí.

Así, fijado un sistema de ejes cartesianos —en otras palabras, un puntoorigeny unabase— un vector tridimensional queda completamente determinado por tres números, llamadoscoordenadas cartesianas.Más concretamente, dados tres números$(x,y,z)$se puede trazar unaflechao vector siguiendo estos pasos:

1. Desplazarse$x$unidades en la dirección del eje$X$.
2. Desplazarse$y$unidades en la dirección del eje$Y$.
3. Desplazarse$z$unidades en la dirección del eje$Z$.
4. Trazar la flecha desde el punto origen hasta el de llegada.

En matemáticas se define vector como un elemento de unespacio vectorial.Esta noción es más abstracta, ya que para muchos espacios vectoriales no es posible representar sus vectores mediante el módulo y la dirección. En particular los espacios dedimensión infinitasinproducto escalarno son representables de ese modo. Los vectores en un espacio euclidiano se pueden representar geométricamente como segmentos de recta$\mathbb {R}$,en el plano$\mathbb {R} ^{2}$(bidimensional), o en el espacio$\mathbb {R} ^{3}$(tridimensional).

Por lo tanto, la definición usada en física de vector como un segmento de recta orientado (en el plano o en el espacio) es un caso particular de esta noción. Es posible describir fenómenos físicos mediante magnitudes físicas vectoriales como las siguientes:

• Lavelocidadde unautomóvil.No sería suficiente describirla con tan solo unnúmero,que es lo que marca elvelocímetro,sino que se requiere indicar la dirección (hacia donde se dirige).
• Lafuerzaque actúa sobre un objeto, ya que su efecto depende, además de su magnitud o módulo, de la dirección en la que actúa.
• Eldesplazamientode un objeto, pues es necesario definir la distancia que recorre, y la dirección del movimiento, o bien la posición inicial y final del objeto.

Conceptos fundamentales en vectores euclídeos

Esta sección explica los aspectos básicos, la necesidad de los vectores para representar ciertas magnitudes físicas, los componentes de un vector euclídeo o geométrico, así como la notación de los mismos, etc. En otra sección más adelante se tratan otro tipo de vectores más generales.

Definición

Componentes de un vector.

Un vector es un elemento de un espacio vectorial. En la práctica, cuando se tratan con vectores usualmente se expresan a unabase vectorial.Así fijada un espacio vectorial específico y una base dentro del mismo:

Unvector (real)de dimensión$n\,$viene representado por unatupladenúmeros reales(que se llaman componentes del vector). El conjunto de todos los vectores dedimensión$n$se representa como$\mathbb {R} ^{n}$(formado mediante elproducto cartesiano). Así, un vector$\scriptstyle v$perteneciente a un espacio$\mathbb {R} ^{n}$se representa como:

$v=(a_{1},a_{2},a_{3},\dots,a_{n})$,donde$v\in \mathbb {R} ^{n}$

Un vector también se puede ver desde el punto de vista de lageometríacomovector geométrico(usando frecuentemente el espacio tridimensional$\mathbb {R} ^{3}$o bidimensional$\mathbb {R} ^{2}$).

Un vector fijo del plano euclidiano es un segmento orientado, en el que hay que distinguir tres características:​​​

• Módulo: la longitud del segmento expresado en términos de un valor numérico y una unidad.
• Dirección: el ángulo u orientación angular del vector con respecto al eje x. Una dirección puede ser recorrida en dos sentidos opuestos (por ej. puede tener una orientación norte-sur, este-oeste, vertical, horizontal, paralela, etc.).
• Sentido: es cada una de las dos orientaciones opuestas de una misma dirección, indicando el origen y extremo (representado en general con la punta de una flecha en un vector) de ésta. Puede ser positivo o negativo.

En inglés, la palabradirectionindica tanto la dirección como el sentido del vector, con lo que se define el vector con solo dos características: módulo y dirección.​

Los vectores fijos del plano se denotan con dos letras mayúsculas (y una flecha hacia la derecha encima), por ejemplo${\overrightarrow {AB}}$,que indican su origen y extremo respectivamente. Es decir, el punto A es el origen o punto de aplicación y el punto B es el extremo del vector${\overrightarrow {AB}}$,cuyas coordenadas son:

${\overrightarrow {AB}}=(x_{B}-x_{A},y_{B}-y_{A})\,$

Características de un vector

Coordenadas cartesianas.

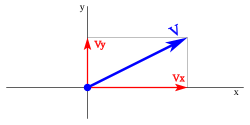
Un vector se puede definir por suscoordenadas,si el vector está en el plano xy, se representa:

${\textstyle {\vec {V}}={\boldsymbol {V}}=(V_{x},V_{y})}$

siendo sus coordenadas:

$V_{x},\;V_{y}$

Si consideramos el triángulo formado por los componentes$V_{x},V_{y}$(como catetos) y$V$(como hipotenusa): se puede calcular$V_{x}$multiplicando$V$por el$\cos(\ Alpha )$(siendo el ángulo formado por$V_{x}$y$V$) o multiplicando$V$por el$\operatorname {sen}(\beta )$(siendo$\beta$el ángulo formado por$V_{y}$y$V$). De igual forma se puede calcular$V_{y}$multiplicando$V$por el$\operatorname {sen}(\ Alpha )$o multiplicando$V$por el$\cos(\beta )$(considerando las posiciones de$\ Alpha$y$\beta$mencionadas anteriormente).

Siendo el vector la suma vectorial de sus coordenadas:

${\vec {V}}={\vec {V_{x}}}+{\vec {V_{y}}}$

Coordenadastridimensionales.

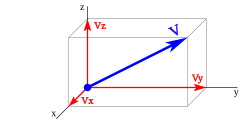
Si un vector es de tres dimensiones reales, representado sobre los ejes x, y, z, se puede representar:

${\vec {V}}={\boldsymbol {V}}=(V_{x},V_{y},V_{z})$

siendo sus coordenadas:

$V_{x},\;V_{y},\;V_{z}$

Si representamos el vector gráficamente podemos diferenciar los siguientes elementos:

La recta soporte odirección,sobre la que se traza el vector.

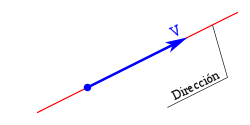
Elmóduloo amplitud con una longitud proporcional al valor del vector.

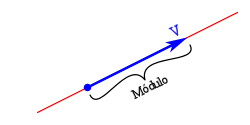
Elsentido,indicado por la punta de flecha, siendo uno de los dos posibles sobre la recta soporte.

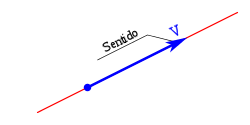
Elpunto de aplicaciónque corresponde al lugar geométrico al cual corresponde la característica vectorial representado por el vector.

Elnombreo denominación es la letra, secuencia o signo de signos que define al vector.

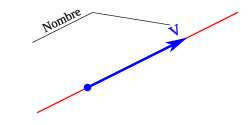
Por lo tanto en un vector podemos diferenciar:

Nombre

Dirección

Sentido

Módulo

Punto de aplicación

Magnitudes vectoriales

Representación gráfica de una magnitud vectorial, con indicación de su punto de aplicación y de los versores cartesianos.

Representación de los vectores.

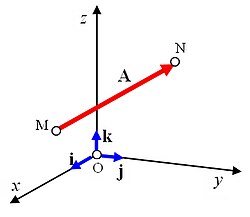
Frente a aquellas magnitudes físicas, tales como lamasa,lapresión,elvolumen,laenergía,latemperatura,etc; que quedan completamente definidas por un número y las unidades utilizadas en su medida, aparecen otras, tales como eldesplazamiento,lavelocidad,laaceleración,lafuerza,elcampo eléctrico,etc., que no quedan completamente definidas dando un dato numérico, sino que llevan asociadas una dirección. Estas últimas magnitudes son llamadasvectorialesen contraposición a las primeras llamadasescalares.

Las magnitudes vectoriales quedan representadas por un ente matemático que recibe el nombre de vector. En unespacio euclidiano,de no más de tres dimensiones, un vector se representa por un segmento orientado. Así, un vector queda caracterizado por los siguientes elementos: su longitud omódulo,siempre positivo por definición, y sudirección,la cual puede ser representada mediante la suma de suscomponentes vectorialesortogonales, paralelas a los ejes de coordenadas; o mediantecoordenadas polares,que determinan el ángulo que forma el vector con los ejes positivos de coordenadas.​ ​

Se representa como un segmento orientado, con una dirección, dibujado de forma similar a una "flecha". Su longitud representa el módulo del vector, la recta indica la dirección, y la "punta de flecha" indica su sentido.​​​

Notación

Las magnitudes vectoriales se representan en los textos impresos por letras ennegrita,para diferenciarlas de las magnitudes escalares que se representan encursiva.En los textos manuscritos, las magnitudes vectoriales se representan colocando una flecha sobre la letra que designa su módulo (el cual es unescalar).

Ejemplos

• $\mathbf {A},\ \mathbf {a},\ {\boldsymbol {\ Omega }},$…representan, respectivamente, las magnitudes vectoriales de módulosA,a,ω,…El módulo de una magnitud vectorial también se representa encerrando entre barras la notación correspondiente al vector:$|\mathbf {A} |,\ |\mathbf {a} |,\ |{\boldsymbol {\ Omega }}|,$…
• En los textos manuscritos se escribe:${\vec {A}},\ {\vec {a}},\ {\vec {\ Omega }},$…para los vectores y$|{\vec {A}}|,\ |{\vec {a}}|,\ |{\vec {\ Omega }}|,$…o$A,\ a,\ {\ Omega },$…para los módulos.

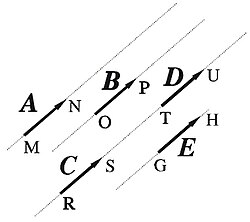
Cuando convenga, se representan la magnitud vectorial haciendo referencia al origen y al extremo del segmento orientado que la representa geométricamente; así, se designan los vectores representados en la Figura 2 en la forma$\mathbf {A} ={\overrightarrow {MN}},\mathbf {B} ={\overrightarrow {OP}}\,$,…resultando muy útil esta notación para los vectores que representan el desplazamiento.

Además de estas convenciones losvectores unitarioso versores, cuyomóduloes la unidad, se representan frecuentemente con un circunflejo encima, por ejemplo$\mathbf {\hat {u}},\mathbf {\hat {v}}$.

Clasificación de vectores

Según los criterios que se utilicen para determinar la igualdad oequipolenciade dos vectores, pueden distinguirse:

• Vectores libres: no están aplicados en determinado punto.
• Vectores deslizantes: su punto de aplicación puede deslizar a lo largo de su recta de acción.
• Vectores fijos o ligados: están aplicados en un determinado punto.

Podemos referirnos también a:

• Vectores unitarios: vectores de módulo uno.
• Vectores concurrentes o angulares: vectores cuyas direcciones o líneas de acción pasan por un mismo punto. También se les suele llamar angulares porque forman un ángulo entre ellas.
• Vectores opuestos: vectores de igual magnitud y dirección, pero sentidos contrarios.​ En inglés se dice que son de igual magnitud pero direcciones contrarias, ya que la dirección también indica el sentido.
• Vectores colineales: vectores que comparten una misma recta de acción.
• Vectores paralelos: vectores cuyas líneas de acción son paralelas.
• Vectores coplanarios: vectores cuyas rectas de acción son coplanarias (situadas en un mismo plano).
• Vectores Perpendiculares: son dos vectores que forman un ángulo de 90 grados y su producto escalar es cero.

Componentes de un vector

Componentes del vector.

Un vector en el espacio euclidiano tridimensional se puede expresar como unacombinación linealde tresvectores unitarioso versores, que son perpendiculares entre sí y constituyen unabase vectorial.

En coordenadas cartesianas, los vectores unitarios se representan por$\mathbf {i} \,$,$\mathbf {j}$,$\mathbf {k}$,( ou,v,w) paralelos a los ejes$x$,$y$,$z$correspondientes. Los componentes del vector en una base predeterminada pueden escribirse entre paréntesis y separadas con comas:

$\mathbf {a} =(a_{x},a_{y},a_{z})$

o expresarse como una combinación de los vectores unitarios definidos en la base vectorial. Así, en un sistema de coordenadas cartesiano, será

$\mathbf {a} =a_{x}\,\mathbf {i} +a_{y}\,\mathbf {j} +a_{z}\,\mathbf {k}$

Estas representaciones son equivalentes entre sí, y los valores$a_{x}$,$a_{y}$,$a_{z}$,son los componentes de un vector que, salvo que se indique lo contrario, sonnúmeros reales.

Una representación conveniente de las magnitudes vectoriales es mediante unvector columnao unvector fila,particularmente cuando están implicadas operacionesmatrices(tales como el cambio de base), del modo siguiente:

$\mathbf {a} ={\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\\\end{bmatrix}}\qquad \mathbf {a} =[a_{x}\ a_{y}\ a_{z}]$

Por ejemplo, los vectores unitarios se expresarían de la siguiente manera:

${\mathbf {i} }=[1\ 0\ 0],\ {\mathbf {j} }=[0\ 1\ 0],\ {\mathbf {k} }=[0\ 0\ 1]$

Ellema de Zorn,consecuencia delaxioma de elección,permite establecer que todo espacio vectorial admite unabase vectorial,por lo que todo vector es representable como el producto de unos componentes respecto a dicha base. Dado un vector, solamente existen un número finito de componentes diferentes de cero.

Representación gráfica de los vectores

Hay personas que no recomiendan usargráficospara evitar la confusión de conceptos y la inducción al error, sin investigación que lo corrobore, también es cierto que la memoria se estimula con mejores resultados. Para ello:

• Se llama vector a larepresentación visualcon el símbolo de flecha (un segmento y un triángulo en un extremo).
• La rectitud visual de una flecha o curvatura de la misma, no la hace diferente en símbolo si los dos extremos permanecen en el mismo lugar y orden.
• El que una flecha cierre en sí misma, indica la ausencia de efectosalgebraicos.
• Para visualizar la suma de vectores se hará encadenándolos, es decir, uniendo el extremo que tiene un triángulo (final) del primer vector con el extremo que no lo tiene (origen) del segundo vector manteniendo la dirección y distancia, propias al espacio, de sus dos extremos, ya que estas dos cualidades los distingue visualmente de otros vectores.
• Losescalaresse representarán con una línea de trazos a modo, exclusivamente, de distinción ya que no siempre pertenecen alespacio de vectores.

Se examinan cada uno de los casos que aparecen en la definición de las operaciones suma de vectores y producto por un escalar:

Suma de vectores

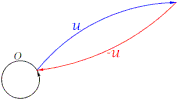
La definición suma de vectores en el ordenu+vproduce otro vector, es como encadenar, siempre visualmente, un vectoruy luego unov.Diremos queu+vse simplifica como un vectorwo quewdescompone como suma de vectoresuyv.

1) Decir queu+v=v+u,es exigir que las dos sumas simplifiquen en el mismo vector, en negro. Véase que en física los vectores en rojo simulan la descomposición de fuerzas ejercidas por el vector negro en su origen, y se representa con unparalelogramo.

2) Decir queu+(v+w)=(u+v)+w,es exigir que las simplificaciones de sumas de vectores puedan ser optativas en cualquier cadena de sumas.

3) Decir que existe un vector cero (elemento neutro) tal queu+0=u,equivale a exigir que exista un vector incapaz de efectuar, mediante la suma, modificación alguna a todos los vectores.

4) Decir queu+(-u)=0, es exigir la existencia de unelemento opuesto,-u,que sumado ausimplifique en unvector cero.

Producto por un escalar

La definición producto por un escalar$a\cdot u$produce otro vector; es como modificar el extremo final del vectoru,siempre visualmente.

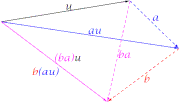
Por un lado, la representación del producto en el caso de que elcuerpode los escalares sea$K=\mathbb {R}$modifica, visualmente, la longitud de la imagen del vector, quedando ambos siempre superpuestos; por otro lado, las representaciones en el caso de que$K=\mathbb {C}$además de modificar la longitud, también agregarotaciones,para facilitarlas visualmente considérense centradas en el origen del vector, siendo estas modificaciones un poco más expresivas, visualmente, pero no más fáciles que en el caso real:

a)Decir quea(bu)=(ab)u,es exigir que los productos encadenadosa(b(u)) pueden simplificarse como uno,c=ab,luego (ab)uqueda comocu.

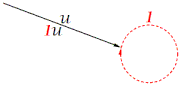
b) Decir que existe el escalar 1 tal que 1u=u,equivale a decir exista un escalar incapaz de efectuar, mediante producto, modificación alguna a todos los vectores.

c) Decir quea(u+v)=au+av,es exigir lapropiedad distributivarespecto lasuma vectorial.

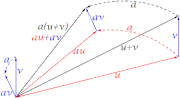
d) Decir que (a+b)u=au+bu,es exigir la propiedad distributiva respecto la suma escalar.

Para el caso real se han de eliminar las rotaciones de los ejemplos anteriores.

Operaciones con vectores euclídeos

Suma de vectores

Para sumar dos vectores libres (vector y vector) se escogen como representantes dos vectores tales que el extremo final de uno coincida con el extremo origen del otro vector.

Suma de vectores sobre un mismo punto

La suma de vectores está bien definida si ambos vectores pertenecen al mismo espacio vectorial, en física para que dos vectores puedan ser sumados deben estar aplicados en el mismo punto. La composición de fuerzas sobre unsólido rígidocuando los puntos de aplicación no coinciden lleva a la noción demomento de fuerzadados dos fuerzas$\scriptstyle \mathbf {F} _{1},\mathbf {F} _{2}$con puntos de aplicación$\scriptstyle \mathrm {P} _{1},\mathrm {P} _{2}$se definen lafuerza resultantecomo el par:^{[cita requerida]}

$(\mathrm {P} _{R},\mathbf {F} _{R})=(\mathrm {P} _{1},\mathbf {F} _{1})\boxplus (\mathrm {P} _{2},\mathbf {F} _{2})$

Donde$\boxplus$es la suma generalizada a vectores aplicados en diferentes puntos. El punto de aplicación$\scriptstyle \mathrm {P} _{R}$es el punto de intersección de las rectas de acción de las fuerzas. Los componentes del vector de fuerza resultante es de hecho la suma de componentes ordinarias de vectores:

$(\mathrm {P} _{R},\mathbf {F} _{R})=(\mathrm {P} _{R},\mathbf {F} _{1}+\mathbf {F} _{2})$

Elmomento resultantees elmomento de fuerzadel conjunto de fuerzas respecto al punto calculado para la fuerza resultante.

Método del paralelogramo

Método del paralelogramo.

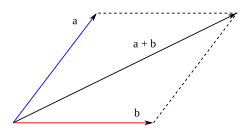
Este método permite solamente sumar vectores de dos en dos. Consiste en disponer gráficamente los dos vectores de manera que los orígenes de ambos coincidan en un punto, trazando rectas paralelas a cada uno de los vectores, en el extremo del otro y de igual longitud, formando así unparalelogramo(ver gráfico). El vector resultado de la suma es la diagonal de dicho paralelogramo que parte del origen común de ambos vectores.

Método del triángulo o método poligonal

Método del triángulo.

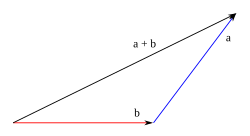
Consiste en disponer gráficamente un vector a continuación de otro, ordenadamente: el origen de cada uno de los vectores coincidirá con el extremo del siguiente. El vector resultante es aquel cuyo origen coincide con el del primer vector y termina en el extremo del último.

Método analítico para la suma y diferencia de vectores

Dados dos vectores libres,

$\mathbf {a} =(a_{x}\mathbf {i} +a_{y}\mathbf {j} +a_{z}\mathbf {k} )$

$\mathbf {b} =(b_{x}\mathbf {i} +b_{y}\mathbf {j} +b_{z}\mathbf {k} )$

El resultado de su suma o de su diferencia se expresa en la forma

$\mathbf {a} \pm \mathbf {b} =(a_{x}\mathbf {i} +a_{y}\mathbf {j} +a_{z}\mathbf {k} )\pm (b_{x}\mathbf {i} +b_{y}\mathbf {j} +b_{z}\mathbf {k} )$

y ordenando los componentes,

$\mathbf {a} \pm \mathbf {b} =(a_{x}\pm b_{x})\mathbf {i} +(a_{y}\pm b_{y})\mathbf {j} +(a_{z}\pm b_{z})\mathbf {k}$

Con la notación matricial sería

$\mathbf {a} \pm \mathbf {b} ={\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\\\end{bmatrix}}\pm {\begin{bmatrix}b_{x}\\b_{y}\\b_{z}\\\end{bmatrix}}={\begin{bmatrix}a_{x}\pm b_{x}\\a_{y}\pm b_{y}\\a_{z}\pm bz\\\end{bmatrix}}$

Conocidos los módulos de dos vectores dados,$\mathbf {a}$y$\mathbf {b}$,así como el ángulo$\theta$que forman entre sí, el módulo de$\mathbf {a} \pm \mathbf {b}$es:

$|\mathbf {a} \pm \mathbf {b} |={\sqrt {a^{2}+b^{2}\pm 2ab\cos \theta }}\leq {\sqrt {a^{2}+b^{2}+2ab\cos \theta }}$

La deducción de esta expresión puede consultarse endeducción del módulo de la suma.

Producto de un vector por un escalar

Producto por un escalar.

El producto de un vector por un escalar es otro vector cuyo módulo es el producto del escalar por el módulo del vector, cuya dirección es igual a la del vector, y cuyo sentido es contrario a este si el escalar es negativo.

Partiendo de la representación gráfica del vector, sobre la misma línea de su dirección tomamos tantas veces el módulo de vector como indica el escalar.

Sean$p\,$un escalar y$\mathbf {a}$un vector, el producto de$p\,$por$\mathbf {a}$se representa$p\,\mathbf {a}$y se realiza multiplicando cada una de los componentes del vector por el escalar; esto es,

$p\,\mathbf {a} =pa_{x}\mathbf {i} +pa_{y}\mathbf {j} +pa_{z}\mathbf {k}$

Con la notación matricial sería

$p\,\mathbf {a} =p\,{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\\\end{bmatrix}}={\begin{bmatrix}p\,a_{x}\\p\,a_{y}\\p\,a_{z}\\\end{bmatrix}}$

Derivada ordinaria de un vector

Dado un vector que es función de una variable independiente

$\mathbf {a} (t)=a_{x}(t)\mathbf {i} +a_{y}(t)\mathbf {j} +a_{z}(t)\mathbf {k}$

Calculamos laderivada ordinariadel vector con respecto de la variablet,calculando la derivada de cada una de sus componentes como si de escalares se tratara:

${\frac {d}{dt}}\mathbf {a} (t)={\frac {d}{dt}}a_{x}(t)\mathbf {i} +{\frac {d}{dt}}a_{y}(t)\mathbf {j} +{\frac {d}{dt}}a_{z}(t)\mathbf {k}$

teniendo en cuenta que los vectores unitarios son constantes en módulo y dirección.

Con notación matricial sería

${\frac {d}{dt}}\mathbf {a} (t)={\frac {d}{dt}}\,{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\\\end{bmatrix}}={\begin{bmatrix}{\frac {d}{dt}}a_{x}\\{\frac {d}{dt}}a_{y}\\{\frac {d}{dt}}a_{z}\\\end{bmatrix}}$

$\mathbf {r} (t)=\operatorname {sen}(t)\mathbf {i} +\cos(t)\mathbf {j} +5t\mathbf {k}$

Veamos un ejemplo de derivación de un vector, partiendo de una función vectorial:

$\mathbf {r} (t)=\operatorname {sen}(t)\mathbf {i} +\cos(t)\mathbf {j} +5t\mathbf {k}$

Esta función representa una curva helicoidal alrededor del ejez,de radio unidad, como se ilustra en la figura. Podemos imaginar que esta curva es la trayectoria de una partícula y la función$\mathbf {r} (t)\,$representa el vectorposiciónen función del tiempot.Derivando tendremos:

${\frac {d\mathbf {r} (t)}{dt}}={\frac {d}{dt}}\operatorname {sen}(t)\mathbf {i} +{\frac {d}{dt}}\cos(t)\mathbf {j} +{\frac {d}{dt}}5t\mathbf {k}$

Realizando la derivada:

${\frac {d\mathbf {r} (t)}{dt}}=\cos(t)\mathbf {i} -\operatorname {sen}(t)\mathbf {j} +5\mathbf {k}$

La derivada del vectorposiciónrespecto al tiempo es la velocidad, así que esta segunda función determina el vector velocidad de la partícula en función del tiempo, podemos escribir:

$\mathbf {v} (t)=\cos(t)\mathbf {i} -\operatorname {sen}(t)\mathbf {j} +5\mathbf {k}$

Este vectorvelocidades un vector tangente a la trayectoria en el punto ocupado por la partícula en cada instante. El sentido es hacia los valores crecientes de los valores escalares.​ Si derivásemos de nuevo obtendríamos el vector aceleración.

Derivada covariante de un vector

Cuando en lugar de emplear una "base fija" en todo el dominio de un vector se usan "bases móviles" como cuando se empleancoordenadas curvilíneasla variación total de un vector dependiente del tiempo depende no solo de la variación de componentes como en el caso de la derivada ordinaria sino también de la variación de la orientación de la base. La variación total se llamaderivada covariante:

${\frac {\delta }{\delta t}}\mathbf {a} (t)=\sum _{k}\left({\dot {a}}^{k}\mathbf {e} _{k}+a^{k}{\dot {\mathbf {e} }}_{k}\right)={\frac {d}{dt}}\mathbf {a} (t)+\mathbf {a} (t)\times {\boldsymbol {\ Omega }}(t)$

Cuando se emplea una base fija (coordenadas cartesianas) la derivada covariante coincide con la derivada ordinaria. Por ejemplo cuando se estudia el movimiento de una partícula desde un sistema de referencia no inercial en rotación, las aceleracionesde Coriolisycentrípetase deben a los factores que contienen${\boldsymbol {\ Omega }}$y otros factores menos comunes.

Ángulo entre dos vectores

El ángulo determinado por las direcciones de dos vectores$\mathbf {a}$y$\mathbf {b}$viene dado por:

$\cos \theta ={\frac {\mathbf {a} \cdot \mathbf {b} }{|\mathbf {a} |\,|\mathbf {b} |}}$

Descomposiciones de un vector

Dado un vector$\mathbf {a}$y una dirección de referencia dada por un vector unitario$\mathbf {n}$se puede descomponer el primer vector en un componente paralela y otro componente perpendicular a la dirección de referencia:

$\mathbf {a} =\mathbf {a} _{\|}+\mathbf {a} _{\bot }=(\mathbf {n} \cdot \mathbf {a} )\mathbf {n} +(\mathbf {n} \times \mathbf {a} )\times \mathbf {n}$

En física esta descomposición se usa en diferentes contextos como descomponer la aceleración en un componente paralela a la velocidad y otro componente perpendicular a la misma. También eltensión mecánicaen un punto sobre un plano puede descomponerse en un componente normal al plano y otra paralela.

También dado un campo vectorial$\mathbf {u} (\mathbf {x} )$definido sobre undominio de Lipschitz,acotado,simplemente conexoy decuadrado integrable$\mathbf {u} \in (L^{2}(\Omega ))^{3}$admite la llamadadescomposición Helmholtzcomo suma de uncampo conservativoy uncampo solenoidal:

$\mathbf {u} =\mathbf {u} _{C}+\mathbf {u} _{S}=({\boldsymbol {\nabla }}\varphi )+({\boldsymbol {\nabla }}\times \mathbf {A} )$

Cambio de base vectorial

Cambio de base vectorial.

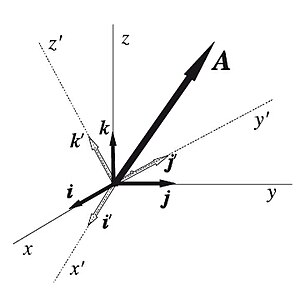
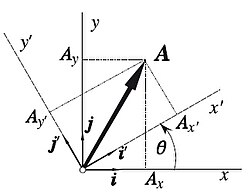
Enmatemáticaslas rotaciones sontransformaciones linealesque conservan las normas enespacios vectorialesen los que se ha definido una operación deproducto interno.Lamatrizde transformación tiene la propiedad de ser una matriz unitaria, es decir, esortogonaly sudeterminantees 1. Sea un vector$\scriptstyle \mathbf {A}$expresado en un sistema de coordenadas cartesianas (x, y, z) con una base vectorial${\mathcal {B}}$asociada definida por los versores$\left(\mathbf {i},\mathbf {j},\mathbf {k} \,\right)$;esto es,

$\mathbf {A} ={\begin{bmatrix}A_{x}\\A_{y}\\A_{z}\end{bmatrix}}_{\mathcal {B}}$

Ahora, supongamos que giramos el sistema de ejes coordenados, manteniendo fijo el origen del mismo, de modo que obtengamos un nuevo triedro ortogonal de ejes (x′, y′, z′), con una base vectorial${\mathcal {B}}'$asociada definida por los versores$\left(\mathbf {i} ',\mathbf {j} ',\mathbf {k} '\,\right)$.Los componentes del vector$\mathbf {A} \,$en esta nueva base vectorial serán:

$\mathbf {A} ={\begin{bmatrix}A'_{x}\\A'_{y}\\A'_{z}\end{bmatrix}}_{{\mathcal {B}}'}$

La operación de rotación de la base vectorial siempre puede expresarse como la acción de un operador lineal (representado por una matriz) actuando sobre el vector (multiplicando al vector):

$\mathbb {R} \,\mathbf {A} _{\mathcal {B}}=\mathbf {A} _{{\mathcal {B}}'}$

que es la matriz de transformación para el cambio de base vectorial.

Cambio de base vectorial.

Ejemplo

En el caso simple en el que el giro tenga magnitud$\theta \,$alrededor del ejez,tendremos la transformación:

$\mathbb {R} ={\begin{bmatrix}\cos \theta &\operatorname {sen} \theta &0\\-\operatorname {sen} \theta &\cos \theta &0\\0&0&1\\\end{bmatrix}}$

Al hacer la aplicación del operador, es decir, al multiplicar la matriz por el vector, obtendremos la expresión del vector$\mathbf {A} \,$en la nueva base vectorial:

${\begin{bmatrix}\cos \theta &\operatorname {sen} \theta &0\\-\operatorname {sen} \theta &\cos \theta &0\\0&0&1\\\end{bmatrix}}{\begin{bmatrix}A_{x}\\A_{y}\\A_{z}\end{bmatrix}}_{\mathcal {B}}={\begin{bmatrix}A'_{x}\\A'_{y}\\A'_{z}\end{bmatrix}}_{{\mathcal {B}}'}$

siendo

$A'_{x}=A_{x}\cos \theta +A_{y}\operatorname {sen} \theta \,$

$A'_{y}=-A_{x}\operatorname {sen} \theta +A_{y}\cos \theta \,$

$A'_{z}=A_{z}\,$

los componentes del vector en la nueva base vectorial.

Vectores en el caso general

En matemáticas, se define la estructura deespacio vectorialy a cada uno de los elementos o puntos de ese espacio se les denominavector.En muchos casos los vectores no pueden ser representados por módulo dirección y sentido. Por ejemplo, en unespacio vectorial complejosobre losnúmeros complejosla noción de módulo no está automáticamente defindida. Igualmente en un espacio vectorial dedimensión infinita,como es el caso deespacios de Hilbertno existe una representación gráfica de los vectores como segmentos orientados.

Requerimientos físicos de las magnitudes vectoriales

No cualquiern-tuplade funciones o números reales constituye un vector físico. Para que unan-tupla represente un vector físico, los valores numéricos de los componentes del mismo medidos por diferentesobservadoresdeben transformarse de acuerdo con ciertas relaciones fijas.

En mecánica newtoniana generalmente se utilizan vectores genuinos, llamados a veces vectores polares, junto con pseudovectores, llamadosvectores axialesque realmente representan eldual de Hodgede magnitudes tensoriales antisimétricas. Elmomento angular,elcampo magnéticoy todas las magnitudes en cuya definición interviene elproducto vectorialson en realidad pseudovectores ovectores axiales.

Enteoría de la relatividad especial,solamente losvectores tetradimensionalescuyas medidas tomadas por diferentes observadores pueden ser relacionadas mediante algunatransformación de Lorentzconstituyen magnitudes vectoriales. Así los componentes de dos magnitudes vectoriales medidas por dos observadores$O\,$y${\bar {O}}$deben relacionarse de acuerdo con la siguiente relación:

${\bar {V}}^{\beta }=\sum _{\ Alpha =0}^{3}\Lambda _{\ Alpha }^{\beta }\ V^{\ Alpha }$

Donde$\Lambda _{\ Alpha }^{\beta }$son los componentes de la matriz que da la transformación de Lorentz. Magnitudes como elmomento angular,elcampo eléctricoo elcampo magnéticode hecho en teoría de la relatividad no son magnitudes vectoriales sinotensoriales.

Véase también

• Vector (matemáticas y física)
• Producto escalar
• Producto vectorial
• Doble producto vectorial
• Producto mixto
• Producto tensorial
• Combinación lineal
• Sistema generador
• Dependencia e independencia lineal
• Base (álgebra)
• Ortogonalidad (matemática)
• Base ortonormal
• Geometría analítica

Bibliografía

• Ortega, Manuel R. (1989-2006).Lecciones de Física (4 volúmenes).Monytex.ISBNISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7.
• Resnick, Robert & Krane, Kenneth S. (2001).Physics(en inglés).New York: John Wiley & Sons.ISBN0-471-32057-9.
• Serway, Raymond A.; Jewett, John W. (2004).Physics for Scientists and Engineers(en inglés)(6.ª edición). Brooks/Cole.ISBN0-534-40842-7.
• Tipler, Paul A. (2000).Física para la ciencia y la tecnología (2 volúmenes).Barcelona: Ed. Reverté.ISBN84-291-4382-3.

Enlaces externos

• Wikcionariotiene definiciones y otra información sobrevector.
• Weisstein, Eric W.«Vector».En Weisstein, Eric W, ed.MathWorld(en inglés).Wolfram Research.

• Datos:Q44528
• Multimedia:Vectors/Q44528