Sirge

Sirgeehksirgjoonon ilma läbimõõduta, mõlemas suunas lõpmata pikk, kõverustetajoonehkühemõõtmelineruum,mis võib sisalduda mitmemõõtmelises ruumis.

Sirge tasandil

Üldvõrrand

Sirge üldvõrrandtasandilon (Descartesikoordinaadistikus) ristkoordinaadistikuslineaarvõrrand$Ax+By+C=0$,kus$A$,$B$ja$C$onkonstandid,kusjuures$A$ja$B$ei võrdu samaaegselt nulliga.

Näide

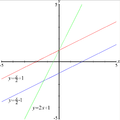
Sirge võrrand tasandil:

$4x-1y-1=0{\text{ ehk }}y=4x-1$

Parameetriline kuju

Kasutatakse üldvõrrandi$Ax+By+C=0$parameetrilist kuju$L=\left\{{\begin{array}{c}x=x_{0}+ta\\y=y_{0}+tb\end{array}}\right.{\text{, kus }}t\in \mathbb {R}$

Näide

$\mathbb {R} ^{2}$,kus sirge on määratud 2 vektori kaudu$\alpha =\left({\begin{array}{c}2\\4\end{array}}\right){\text{ ja }}\beta =\left({\begin{array}{c}3\\3\end{array}}\right)$:

$L={a+t({\overrightarrow {\beta -\alpha }}),{\text{ kus }}t\in \mathbb {R} }={\left({\begin{array}{c}2+t\\4-t\end{array}}\right),{\text{ kus }}t\in \mathbb {R} }$

või

$L={b+t({\overrightarrow {\beta -\alpha }}),{\text{ kus }}t\in \mathbb {R} }={\left({\begin{array}{c}3+t\\3-t\end{array}}\right),{\text{ kus }}t\in \mathbb {R} }$

Lisaks eelnimetatule on võimalik parameetrilist kuju tähistada, kui parameetrilisi võrrandeid

$L=\left\{{\begin{array}{c}x_{1}=a_{1}+ts_{1}\\x_{2}=a_{2}+ts_{2}\end{array}}\right.{\text{, kus }}t\in \mathbb {R} =\left\{{\begin{array}{c}x_{1}=3+t\\x_{2}=3-t\end{array}}\right.{\text{, kus }}t\in \mathbb {R}$

ja (Descartesikujul) ehk kanoonilisel kujul

${\frac {x_{1}-a_{1}}{s_{1}}}={\frac {x_{2}-a_{2}}{s_{2}}}\to {\frac {x_{1}-2}{1}}={\frac {x_{2}-4}{-1}}\to x_{1}=-x_{2}+6$

Joonised

• 
  Võrrandiga$y=4x-1$määratud sirge.
• 
  Parameetrilise võrranditega$x_{1}=3+t$,${\displaystyle.x_{2}=3-t}$määratud sirge.
• 
  Sirged tasandil.

Omadused

Olgu antud sirged$u$ja$v$,ning nendele vastavad sihivektorid${\vec {s}}_{1}$ja${\vec {s}}_{2}$.

Ristuvad sirged

Sirged on risti parajasti siis, kui nende sihivektorite tadamskalaarkorrutison$0$:

${\vec {s}}_{1}\cdot {\vec {s}}_{2}=0$

Paralleelsed sirged

Sirged on paralleelsed parajasti siis, kui nende sihivektoriteskalaarkorrutisemoodul on$1$:

$|{\vec {s}}_{1}\cdot {\vec {s}}_{2}|=1$

Kahte punkti saab läbida vaid üks sirge

Eukleidese geomeetriasläbib kahte eripunktiparajasti üks sirge.

Määratud

tõusu ja algordinaadiga

Tõusu (k) jaalgordinaadiga(a) määratud sirge võrrand tasandil:

$y=kx+a$.

kahe punktiga

Kahepunktigamääratudsirgevõrrandtasandil:

${\frac {y-y_{1}}{y_{2}-y_{1}}}={\frac {x-x_{1}}{x_{2}-x_{1}}}$.

punkti ja sihivektoriga

Punkti jasihivektorigamääratud sirge võrrand tasandil:

${\frac {y-y_{1}}{s_{y}}}={\frac {x-x_{1}}{s_{x}}}$.

punkti ja tõusuga

Punktijatõusugamääratud sirgevõrrandtasandil:

$y-y_{1}=k(x-x_{1})$.

kahe tasandi lõikena

Kahe tasandi$\Pi _{1}:\mathbf {n} _{1}\cdot \mathbf {r} =h_{1}$ja$\Pi _{2}:\mathbf {n} _{2}\cdot \mathbf {r} =h_{2}$lõike sirge, kus$\mathbf {n} _{i}$onnormaal vektor,on antud

$\mathbf {r} =(c_{1}\mathbf {n} _{1}+c_{2}\mathbf {n} _{2})+\lambda (\mathbf {n} _{1}\times \mathbf {n} _{2})$

kus

$c_{1}={\frac {h_{1}-h_{2}(\mathbf {n} _{1}\cdot \mathbf {n} _{2})}{1-(\mathbf {n} _{1}\cdot \mathbf {n} _{2})^{2}}}$

$c_{2}={\frac {h_{2}-h_{1}(\mathbf {n} _{1}\cdot \mathbf {n} _{2})}{1-(\mathbf {n} _{1}\cdot \mathbf {n} _{2})^{2}}}.$

Rakendatavad funktsioonid

Sirge kaugus punktist ℝ³ruumis

Olgu antud sirge$u$ja punkt$D(x_{1};y_{1};z_{1})$.Olgu sirge$u$sihivektoriks${\overrightarrow {s}}=(s_{x};s_{y};s_{z})$,siis leiame punkti$X=(x;y;z)$sirgel, mis asub sirgel$u$ja mille kaugus on vähim punkti$D(x_{1};y_{1};z_{1})$.Selleks lahendame võrrandid:

${\frac {x-x_{1}}{s_{x}}}={\frac {y-y_{1}}{s_{y}}}={\frac {z-z_{1}}{s_{z}}}$

Siis leiame vektori${\overrightarrow {DX}}$ja selle pikkuse$r=\left|\left|{\overrightarrow {DX}}\right|\right|$,mis on punkti kaugus sirgest:

$r={\sqrt {\left(x-x_{1}\right){}^{2}+\left(y-y_{1}\right){}^{2}+\left(z-z_{1}\right){}^{2}}}$

Sirgete kaugus ruumis

Olgu antud sirged$u$ja$v$.Sellest leiame vastavad sihivektorid${\overrightarrow {s_{1}}}$ning${\overrightarrow {s_{2}}}$ja suvalised punktid mõlemal sirgel vastavalt$A$ja$B$.

Paralleelsed sirged

$\varrho ={\frac {\left|\left|{\overrightarrow {s_{1}}}\times {\overrightarrow {\text{AB}}}\right|\right|}{\left|\left|{\overrightarrow {s_{1}}}\right|\right|}}$

Kiivsirged

$\varrho (u,v)={\frac {\left|({\overrightarrow {s_{1}}}\times {\overrightarrow {s_{2}}})\cdot {\overrightarrow {\text{AB}}}\right|}{\left|\left|{\overrightarrow {s_{1}}}\times {\overrightarrow {s_{2}}}\right|\right|}}$

Puutuja

$y-y_{1}={\frac {}{}}(f'(x))(x-x_{1})$

Normaal

$y-y_{1}=\left({\frac {-1}{f'(x)}}\right)(x-x_{1})$

Vaata ka

• Tuletis
• Punkt
• Sirgete lõikumine
• Kiir
• Lõik