Suhde

x:n ja y:n suhde.

Suhdetarkoittaamatematiikassakahdenluvuntaisuureenjakolaskua,jonka tarkoitus on verrata kahta lukua tai suuretta keskenään. Suhde merkitään yleensä näkyviin ohjeeksi, johon vertaamalla voidaan muodostaa uusia, mutta toisiinsa samalla tavalla suhtautuvia, lukuja tai suureta. Joskus suhde onmittalukuelisuhdeluku,jossa edellinen suure mitataan jälkimmäisellä suureella.

Kaksoispistettä käytetään ilmaistaessa lukujen tai suureiden suhdetta. Tällöin sen ympärille ei standardin SFS 4175 mukaan kirjoiteta välilyöntejä, toisin kuin käytettäessä kaksoispistettä jako­las­kun merkkinä. Säännön rikkominen ilmaisun luontevuuden takia voi kuitenkin olla perusteltua (esi­mer­kik­si” 1: 20 000” ). Kahden luvunajabsuhde merkitääna:bja lausutaan "a:n suhde b:hen",ja esimerkiksi silloin 5:3 on"viiden suhde kolmeen".Toinen merkintätapa on käyttää jakoviivaa ja esittää suhde lukujen murtolausekkeena tai kokonaislukujen tapauksessa murtolukuna. Silloin

$a:b={\frac {a}{b}}=k$,

missäkonsuhdeluku.Suhdeluvulla ei ole mittayksikköä. Suhteessaaon ensimmäinen jabtoinen suure.

Koska suhteilla on murtolausekkeen rakenne, voidaan niillä laskea samoin kuten murtoluvuilla ja etenkinlaventaminenjasupistaminenovat mahdollisia. Kun kahden lukuparin suhteita verrataan, voidaan niistä muodostaa yhtäsuuressa tapauksessayhtälö,jota kutsutaanverrannoksi

${\frac {a}{b}}=k\land {\frac {c}{d}}=k\Rightarrow {\frac {a}{b}}={\frac {c}{d}}.$

Suhteen arkikäyttöä

Suhteilla voidaan esittää kahden komponentin välisiä suhteita. Kun mehutiivistettä halutaan sekoittaa veteen juoman valmistamiseksi, voidaan antaa ohjeeksi "sekoita mehua ja vettä suhteessa 1:7", jolloin astiaan mitataan yksi lasi tiivistettä ja seitsemän lasia vettä. Myös geometrisiä muotoja voidaan ilmaista suhteilla. Esimerkiksi teräväpiirtotelevisioiden ruutu on eri malleilla eri kokoinen, jolloin ruudun sivujen mittasuhteet elikuvasuhdeilmoitetaan olevan 16:9 (leveys:korkeus).

• 
  Punaisia esiintyy 4: 8 sinisiin nähden.
• 
  Television kuvan sivumitat suhtautuvat kuten 16: 9, aivan kuten myös piirroksessa.
• 
  Sinisiä ja valkoisia on 3: 1 eli sinisiä on${\tfrac {3}{4}}$ja valkoinen on${\tfrac {1}{4}}$kaikista.
• 
  Karttojen mittakaava esittä esimerkiksi 1: 50000 kohteiden etäisyyksiä verrattuna luontoon.

Merkinnän laajennus liittyy yleensä jako-ongelmiin, jossa voitto, palkkio, riski tai perintö jaetaan useampaan kuin kahteen osaan. Esimerkiksi yhdessä tehdyn työn palkka voidaan jakaa työtuntien suhteessa. Silloin kolme työmiestä jakaa urakkapalkkion esimerkiksi suhteessa 47: 35: 12, jolloin kukin saa${\tfrac {47}{94}}$−,${\tfrac {35}{94}}$− ja${\tfrac {12}{94}}$−osan palkkiosta (koska 47 + 35 + 12 = 94).Vedonlyönnissävoittokertoimet ilmaistaan suhteilla. Jos voittokerroin on esimerkiksi 1: 1,67, se vastaa esimerkiksi reseptin lukemista (vrt. 1 osaa mehua 1,67 osaan vettä, eli yht. 2,67 osaa valmista tavaraa). Voiton todennäköisyys on siis${\tfrac {1}{1+1,67}}$.

Mittakaavaon suhteen käyttöä, jossa ilmaistaankartallaolevien mittojen ja luonnonmittojen vastaavuus. Mittakaava 1: 50000 tarkoittaa, että kartalla oleva 1 senttimetrin merkki on luonnossa 50000 senttimetrin eli 500 metrin pituinen kohde.

Suhteen matemaattinen käyttö

Historiallisista syistä johtuen tunnetuimmat suhteet liittyvätgeometrisiinkuvioihin. Tunnetuin suhde onympyränkehänpituuden suhde ympyränhalkaisijaan,jonka suhdeluku on π ≈ 3,14159... elipii.Se on kaikilla ympyröillä sama. Piin tarkka arvo on askarruttanut ihmisiä tuhansia vuosia.

Yhdenmuotoisissa kuvioissakuvion muoto on sama, vaikka koko voi olla erisuuri. Kuvioilla kaikkien vastinsivujen pituuksien suhde on aina sama. Suhdelukua voidaan kutsua muutoskertoimeksi, jolla jälkimmäisen kuvion sivun pituudet saadaan alkuperäisen kuvion pituuksista muutoskertoimella kertomalla.

Kolmionkulman puolittajaleikkaa kulman vastaisen sivun osiin, joiden suhde on sama kuin kulman kylkien eli sivujen pituuksien suhde.

Suorakulmaisen kolmionkulmat määräävät sivujen pituudet ja niiden pituudet riippuvat myös kolmion koosta. Yhdenmuotoisten suorakulmaisten kolmioiden sivujen suhteet ovat sen sijaan samat. Siksi on ollut miellekästä taulukoida sivujen suhteet kolmioiden eri kulmille, jotta voidaan laskea sivujen pituuksia erikokoisille kolmioille.Trigonometristenfunktioiden määrittämät sivusuhteet ovat geometrian tärkeimpiä arkea helpottavia tuloksia. Esimerkiksi kolmiolle, jonka kateetit merkitään a ja b sekä hypotenuusa c, ja jonka terävin kulma on 35°, sivusuhde (sini) on

$k=\sin 35^{\circ }={\tfrac {a}{c}}\approx 0{,}573576436\dots.$

Tämä sivusuhde on siten sama kaililla suorakulmaisille kolmioille, jonka kulma on 35°.

Kultainen leikkaus.

Janan jakaminen osiin voidaan ilmaista suhteilla. Jakopiste jakaa janan kahteen osaan, joiden pituuksien suhde annetaan tai se selvitetään. Jako voidaan suorittaa samalla tavalla myös luvulle. Alkuperäinen luku jaetaan kahdeksi luvuksi, joiden summa on alkuperäinen luku, ja joiden suhde on annettu suhdeluku. Päinvastoin on toimittu, kun lasketaan lukujenkeskiarvo.Silloin keskiarvomjakaa lukujen välin kahteen yhtäsuureen väliin. Esimerkiksi lukujen 4 ja 6 keskiarvomsaadaan suhteesta

${\tfrac {m-4}{6-m}}=1\Leftrightarrow m={\tfrac {4+6}{2}}=5.$

Keskivertokvoidaan määrittää kahden suhteen yhtälöllä eli verrannolla, joka on

${\tfrac {k-4}{6-k}}={\tfrac {4}{k}}\Leftrightarrow k={\sqrt {4\cdot 6}}=2{\sqrt {6}}.$

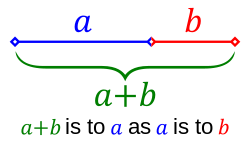
Erityinen suhde onjatkuva suhdeelikultainen suhdeelikultainen leikkaus.Siinä luku tai jana jaetaan kahteen osaan$a$ja$b$,joiden suhde on sama kuin suuremman luvun$a$suhde lukujen summaan$a+b$eli alkuperäiseen lukuun

$a:b=(a+b):a.$

Historia

Pythagoraanliitetään monet helleenisen matematiikan keksinnöt, vaikka hän on todennäköisesti omaksunut nebabylonialaisiltamatkoiltaan sinne. Samaa koskee suhteiden tutkimusta, joita pythagoralaiset tekivät. Esimerkiksi aritmeettinen−, geometrinen− ja harmoninen keskiarvo on opittu näillä matkoilla, mutta Pythagoras ilmeisesti laajensi keskilukujen "teoriaa" keksimällä siihen 7 muutakin keskilukua käyttäen suhteiden ja verrantojen teoriaa. Juuri lukujen suhteita tutkimalla päädyttiinrationaalilukulaskentoonja verrantojen teoriaan. Myöhemmin samoja suhteiden teorioita sovellettiin geometriassa. Kreikkalaiset eivät keksineet suhteiden teoriaa itse. Ne tunnettiin todennäköisesti muuallakin kuin Egyptissä ja Kaksoisvirran maassa, vaikka niistä kertovat dokumentit ovat hävinneet eikä asiaa voi enää vahvistaa.