Identité remarquable

Représentation graphique de l'identité remarquable$(a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}$.

Enmathématiques,on appelleidentités remarquablesou encoreégalités remarquablescertaines égalités qui s'appliquent à desnombres,ou plus généralement à desvariables polynomiales.Elles servent en général à accélérer les calculs, à simplifier certaines écritures, àfactoriserou à développer des expressions. Elles servent pour la résolution deséquations du second degréet sont plus généralement utiles pour la recherche desolutionsd'équations.

La plupart de ces identités remarquables ont tout d'abord été démontrées à l'aide de raisonnementsgéométriques,puis ont été généralisées à despuissancessupérieures par des calculs algébriques. L’une des plus anciennes sources est leLivre II desÉlémentsd’Euclide,propositions 4 et 7.

Identités remarquables du second degré

Dans toute la suite,aetbdésignent des nombres, qui peuvent être desentiers,desrationnelsetréels,ou même descomplexes.Ces identités sont vraies plus généralement dans unanneau commutatif,ou même dans unanneau quelconqueoùaetbcommutent.

Énoncés

Les troisidentités remarquablesdu second degré sont:

$(a+b)^{2}=a^{2}+2ab+b^{2}$ $(a-b)^{2}=a^{2}-2ab+b^{2}$ $(a+b)(a-b)=a^{2}-b^{2}$

La deuxième de ces identités peut être vue comme un cas particulier de la première, en prenant, au lieu deb,–bdans la première égalité. Ces égalités font l'objet d'un vocabulaire spécifique:

Définition d'un produit remarquable—Les trois expressions suivantes sont appeléesproduit remarquable:

$(a+b)^{2},\quad (a-b)^{2}\quad {\text{et}}\quad (a+b)(a-b).$

On définit de même:

Définition d'une somme remarquable—Les trois expressions suivantes sont appeléessomme remarquable:

$a^{2}+2ab+b^{2},\quad a^{2}-2ab+b^{2}\quad {\text{et}}\quad a^{2}-b^{2}.$

Exemples

Développement et réduction

Les identités remarquables permettent de transformer l'écriture de certaines expressions algébriques, comme dans l'exemple suivant:

$A=(2x-3)^{2}+(x+5)(3-x).$

L'expressionAest la somme de deux termes. Le premier terme est un produit remarquable, que l'on peut transformer en somme:

$(2x-3)^{2}=(2x)^{2}-2\times 2x\times 3+3^{2}=4x^{2}-12x+9\quad {\text{et}}\quad A=4x^{2}-12x+9+(x+5)(3-x).$

Le deuxième terme se traite à l'aide de ladistributivitéde la multiplication par rapport à l'addition:

$(x+5)(3-x)=x(3-x)+5(3-x)=3x-x^{2}+15-5x=-x^{2}-2x+15.$

En additionnant termes à termes, on obtient:

$A=4x^{2}-12x+9-x^{2}-2x+15=3x^{2}-14x+24.$

Équation du second degré

Les identités remarquables permettent de résoudre une équation du second degré. Illustrons la méthode sur l'exemple suivant:

$x^{2}+2x-5=0.$

La méthode consiste à travailler la partie de l'expression qui ne dépend pas dexde manière à utiliser une des deux premières identités remarquables et factoriser la partie qui dépend dex:

$x^{2}+2x-5=x^{2}+2x+1-6.$

Les trois premiers termes sont maintenant une somme remarquable, il est possible d'appliquer une identité remarquable et l'équation devient:

$x^{2}+2x-5=(x+1)^{2}-6=(x+1)^{2}-({\sqrt {6}})^{2}=0.$

On reconnaît une nouvelle somme remarquable, l'équation s'écrit encore:

$x^{2}+2x-5=(x+1+{\sqrt {6}})(x+1-{\sqrt {6}})=0.$

Un produita.bde deux nombresaetbest nul si, et seulement si,aoubest nul.Résoudre l'équation revient à résoudre deuxéquations du premier degré:

$(1)\;x+1+{\sqrt {6}}=0\quad {\text{et}}\quad (2)\;x+1-{\sqrt {6}}=0.$

On trouve les deux solutions de l'équation, appelées aussiracines du polynôme:

$x_{1}=-1-{\sqrt {6}}\quad {\text{et}}\quad x_{2}=-1+{\sqrt {6}}.$

La même méthode, appliquée à des coefficients$a$,$b$,et$c$($ax^{2}+bx+c=0$) au lieu des coefficients 1, 2, et –5 de l'exemple précédent, fait apparaitre le rôle dudiscriminantet les deux solutions.

Polynômes au carré

Pour élever au carré un polynôme avec un nombre quelconque de termes, ajouter les carrés de chaque terme individuellement, puis ajouter le double de la somme des produits de chaque paire possible de termes.

$(a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2(ab+ac+bc),$

$(a+b+c+d)^{2}=a^{2}+b^{2}+c^{2}+d^{2}+2(ab+ac+ad+bc+bd+cd).$

Identité remarquable et géométrie

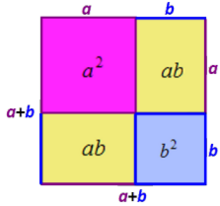
Ces identités remarquables sont connues depuis lesBabyloniens.Il est possible qu'ils se soient rendu compte de ces égalités à l'aide de raisonnements géométriques. Il existe une méthode simple pour trouver la formule suivante:

$(a+b)^{2}=a^{2}+2ab+b^{2}.$

La figure de droite représente un carré. On suppose que la longueur du côté du carré rose est égale àaet celle du carré bleu àb.L'aire du grand carré est égale à (a+b)².
Il existe une autre manière d'exprimer cette aire: elle est la somme des aires des zones rose, bleue et des deux zones jaunes. L'aire rose est égale àa²car c'est un carré de côtéa,l'aire bleue est égale àb²,et chacune des deux aires jaunes est égale àabcar c'est un rectangle de côtésaetb.On obtient bien la formule annoncée.

Démonstration par l'algèbre

L'algèbre permet encore de démontrer ces formules. Calculons (a-b)².Ladistributivitémontre que:

$(a-b)^{2}=(a-b)(a-b)=a(a-b)-b(a-b)=a^{2}-ab-ba+b^{2}=a^{2}-2ab+b^{2}.$

On démontre de même la troisième identité remarquable:

$(a+b)(a-b)=a(a-b)+b(a-b)=a^{2}-ab+ba-b^{2}=a^{2}-b^{2}.$

Identités remarquables diverses

Identité de Brahmagupta

Brahmagupta,unmathématicien indienduVI^esiècledécouvre une identité remarquable du quatrième degré:

$(a^{2}-nb^{2})(c^{2}-nd^{2})=(ac+nbd)^{2}-n(ad+bc)^{2}.$

Il l'utilise dans le cas oùa,b,c,detnsont des nombres entiers. Elle permet de calculer une bonne approximation d'uneracine carrée.

Application au calcul de√3

Brahmagupta remarque que 2²- 3.1²= 1. Il applique son identité plusieurs fois, toujours avecn= 3. La première fois, il posea=c= 2,b=d= 1. Il obtient:

$(2^{2}-3\cdot 1)(2^{2}-3\cdot 1)=(2\cdot 2+3\cdot 1)^{2}-3(2\cdot 1+1\cdot 2)^{2}=7^{2}-3\cdot 4^{2}=1.$

Il recommence avec cette fois avec:a=c= 7,b=d= 4. Il obtient une nouvelle manière d'écrire 1:

$97^{2}-3\cdot 56^{2}=1.$

Il réapplique la même logique, il obtient encore une autre manière d'écrire 1:

$18\,817^{2}-3\cdot 10\,864^{2}=1.$

Cette égalité s'écrit encore:

$18\,817^{2}=3\cdot 10\,864^{2}+1\quad {\text{et}}\quad \left({\frac {18\,817}{10\,864}}\right)^{2}=3+{\frac {1}{10\,864^{2}}}.$

Il obtient une fraction dont le carré est « presque » égal à 3, ce qui revient à dire que 18 817/10 864 est « presque » égal à√3.Si on calcule la fraction, on trouve un résultat dont les neuf premiers chiffres significatifs fournissent la meilleure approximation possible (avec le même nombre de décimales), à savoir: 1,73205081.

Il utilise aussi sa formule pour trouver des solutions à l'équation diophantienneditede Pell-Fermat.

Identité des quatre carrés d'Euler

L'identité des quatre carrés d'Euler relie entre eux huit nombres. Elle prend la forme suivante:

$(a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+a_{4}^{2})(b_{1}^{2}+b_{2}^{2}+b_{3}^{2}+b_{4}^{2})$

$=(a_{1}b_{1}-a_{2}b_{2}-a_{3}b_{3}-a_{4}b_{4})^{2}+(a_{1}b_{2}+a_{2}b_{1}+a_{3}b_{4}-a_{4}b_{3})^{2}$

$+\,(a_{1}b_{3}-a_{2}b_{4}+a_{3}b_{1}+a_{4}b_{2})^{2}+(a_{1}b_{4}+a_{2}b_{3}-a_{3}b_{2}+a_{4}b_{1})^{2}.$

Elle est utilisée, entre autres pour démontrer lethéorème des quatre carrésqui indique que tout nombre entier est somme de quatre carrés.

Identité des huit carrés de Degen

L'identité des huit carrés de Degen relie entre eux seize nombres et a été montrée auXIX^esiècle:

$(a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+a_{4}^{2}+a_{5}^{2}+a_{6}^{2}+a_{7}^{2}+a_{8}^{2})(b_{1}^{2}+b_{2}^{2}+b_{3}^{2}+b_{4}^{2}+b_{5}^{2}+b_{6}^{2}+b_{7}^{2}+b_{8}^{2})=\,$

$(a_{1}b_{1}-a_{2}b_{2}-a_{3}b_{3}-a_{4}b_{4}-a_{5}b_{5}-a_{6}b_{6}-a_{7}b_{7}-a_{8}b_{8})^{2}+\,$

$(a_{1}b_{2}+a_{2}b_{1}+a_{3}b_{4}-a_{4}b_{3}+a_{5}b_{6}-a_{6}b_{5}-a_{7}b_{8}+a_{8}b_{7})^{2}+\,$

$(a_{1}b_{3}-a_{2}b_{4}+a_{3}b_{1}+a_{4}b_{2}+a_{5}b_{7}+a_{6}b_{8}-a_{7}b_{5}-a_{8}b_{6})^{2}+\,$

$(a_{1}b_{4}+a_{2}b_{3}-a_{3}b_{2}+a_{4}b_{1}+a_{5}b_{8}-a_{6}b_{7}+a_{7}b_{6}-a_{8}b_{5})^{2}+\,$

$(a_{1}b_{5}-a_{2}b_{6}-a_{3}b_{7}-a_{4}b_{8}+a_{5}b_{1}+a_{6}b_{2}+a_{7}b_{3}+a_{8}b_{4})^{2}+\,$

$(a_{1}b_{6}+a_{2}b_{5}-a_{3}b_{8}+a_{4}b_{7}-a_{5}b_{2}+a_{6}b_{1}-a_{7}b_{4}+a_{8}b_{3})^{2}+\,$

$(a_{1}b_{7}+a_{2}b_{8}+a_{3}b_{5}-a_{4}b_{6}-a_{5}b_{3}+a_{6}b_{4}+a_{7}b_{1}-a_{8}b_{2})^{2}+\,$

$(a_{1}b_{8}-a_{2}b_{7}+a_{3}b_{6}+a_{4}b_{5}-a_{5}b_{4}-a_{6}b_{3}+a_{7}b_{2}+a_{8}b_{1})^{2}\,$

Identité de Sophie Germain

L'identité deSophie Germainénonce que pour tousnombresxety,on a:

$x^{4}+4y^{4}=(x^{2}+2y^{2})^{2}-4x^{2}y^{2}=(x^{2}+2y^{2}-2xy)(x^{2}+2y^{2}+2xy)=((x+y)^{2}+y^{2})((x-y)^{2}+y^{2}).$

Identité d'Argand

$(x^{2}+x+1)(x^{2}-x+1)=x^{4}+x^{2}+1.$

Identité deGauss

$a^{3}+b^{3}+c^{3}-3abc=(a+b+c)(a^{2}+b^{2}+c^{2}-ab-ac-bc)={\frac {1}{2}}(a+b+c)[(a-b)^{2}+(b-c)^{2}+(a-c)^{2}].$

Identités deLegendre

$(a+b)^{2}+(a-b)^{2}=2(a^{2}+b^{2}),$

$(a+b)^{2}-(a-b)^{2}=4ab,$

$(a+b)^{4}-(a-b)^{4}=8ab(a^{2}+b^{2}).$

Identités deLagrange

$(a^{2}+b^{2})(x^{2}+y^{2})=(ax+by)^{2}+(ay-bx)^{2},$

$(a^{2}+b^{2}+c^{2})(x^{2}+y^{2}+z^{2})=(ax+by+cz)^{2}+(ay-bx)^{2}+(az-cx)^{2}+(bz-cy)^{2}.$

La premièreidentité de Lagrangeici listée est un cas particulier de l'identité de Brahmagupta.

Identités remarquables de degrén

Formule du binôme de Newton

La même technique de démonstration que celle utilisée pour les formules de degré 2 montre que, siaetbdésignent toujours deux nombres:

$(a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3},$

$(a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}.$

Appliqué encore une fois, on obtient:

$(a+b)^{4}=a^{4}+4a^{3}b+6a^{2}b^{2}+4ab^{3}+b^{4},$

$(a-b)^{4}=a^{4}-4a^{3}b+6a^{2}b^{2}-4ab^{3}+b^{4}.$

De même,

$(a+b)^{5}=a^{5}+5a^{4}b+10a^{3}b^{2}+10a^{2}b^{3}+5ab^{4}+b^{5},$

$(a-b)^{5}=a^{5}-5a^{4}b+10a^{3}b^{2}-10a^{2}b^{3}+5ab^{4}-b^{5}.$

On peut la généraliser à un degrénquelconque, à l'aide de la formule du binôme:

$(a+b)^{n}=\sum _{k=0}^{n}{n \choose k}a^{n-k}b^{k}.$

Les coefficients de l'expression, considérée comme unpolynômeenaet enbsont appeléscoefficients binomiaux.Commebpeut prendre une valeur négative, on obtient bien les deux formes précédentes.

La formule s'applique même siaetbne sont pas des nombres. Ces lettres peuvent désignerdeux matrices qui commutent entre elles.De manière générale, la formule est vraie dans unanneau(supposé unitaire, c'est-à-dire muni d'un élément unité$1=a^{0}$pour tout a), si a et b commutent (ce qui est le cas en particulier si a ou b est égal à 1).

Différence ou somme de puissances

Il est aussi possible de généraliser la troisièmeidentité remarquable du second degré.Siaetbdésignent deux nombres:

$a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})$,

$a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})$.

La formule suivante permet de généraliser la démarche. Tout d'abord, pour tout entiern≥ 2, on a la formule deBernoulli^{[Lequel?][réf.souhaitée]}:

$a^{n}-b^{n}=(a-b)(a^{n-1}+a^{n-2}b+\cdots +ab^{n-2}+b^{n-1})=(a-b)\sum _{k=0}^{n-1}a^{n-1-k}b^{k}$.

Cette formule a plusieurs applications importantes, comme une preuve que lafonction puissanceest continue, ou lafactorisation d'un polynôme à partir d'une racine.En remplaçant$b$par$-b$,on en déduit,si n est impair:

$a^{n}+b^{n}=(a+b)(a^{n-1}-a^{n-2}b+\cdots -ab^{n-2}+b^{n-1})=(a+b)\sum _{k=0}^{n-1}(-1)^{k}a^{n-1-k}b^{k}$.

Annexes

Article connexe

• Livre II des Éléments d'Euclide

Liens externes

• Identités remarquables de degré supérieur à 2,sur le site de G. Villemin
• Identités remarquables (Flash),sur le site deSésamath

Bibliographie

• R.Brault,Mathématiques3^e:programme 2008,Paris, Hachette éducation,2008,319p.(ISBN978-2-01-125539-6)— La première partie de l'article s'inspire largement de cette référence.
• (en)Leonard EugeneDickson,History of the Theory of Numbers(en)[détail des éditions],vol. II, Diophantine analysis— Les deux identités remarquables, ainsi que leurs usages en arithmétique sont présents dans cette référence, beaucoup plus technique que la précédente.