Loi binomiale

Loi binomiale
Fonction de masse
Fonction de répartition
Paramètres	$n\in \mathbb {N}$ $p\in [0,1]$
Support	$k\in \{0,\dots,n\}\!$
Fonction de masse	${n \choose k}p^{k}(1-p)^{n-k}\!$
Fonction de répartition	$I_{1-p}(n-\lfloor k\rfloor,1+\lfloor k\rfloor )\!$
Espérance	$np$
Médiane	$\lfloor np\rfloor$ou$\lfloor np\rfloor +1$
Mode	$\lfloor (n+1)\,p\rfloor \!$
Variance	$np(1-p)\!$
Asymétrie	${\frac {1-2p}{\sqrt {npq}}}\!$
Kurtosis normalisé	${\frac {1-6p(1-p)}{np(1-p)}}\!$
Entropie	${\frac {1}{2}}\ln \left(2\pi n\mathrm {e} p(1-p)\right)+O\left({\frac {1}{n}}\right)$
Fonction génératrice des moments	$(1+p(\mathrm {e} ^{t}-1))^{n}\!$
Fonction caractéristique	$(1+p(\mathrm {e} ^{\mathrm {i} t}-1))^{n}\!$
Fonction génératrice des probabilités	$(1+p(t-1))^{n}$

Enthéorie des probabilitéset enstatistique,laloi binomialemodélise la fréquence du nombre de succès obtenus lors de la réalisation de plusieurs expériences aléatoires identiques et indépendantes.

Plus mathématiquement, la loi binomiale est uneloi de probabilité discrètedécrite par deux paramètres:nle nombre d'expériences réalisées, etpla probabilité de succès. Pour chaque expérience appeléeépreuve de Bernoulli,on utilise unevariable aléatoirequi prend la valeur1lors d'un succès et la valeur0sinon. La variable aléatoire, somme de toutes ces variables aléatoires, compte le nombre de succès et suit une loi binomiale. Il est alors possible d'obtenir la probabilité deksuccès dans une répétition denexpériences:

$\mathbb {P} (X=k)={n \choose k}\,p^{k}(1-p)^{n-k}.$

Cette formule fait intervenir lecoefficient binomial${n \choose k}$duquel provient le nom de la loi.

L'importance de cette loi est d'abord historique puisqu'elle a été l'objet d'étude duthéorème de Moivre-Laplace,résultat duxviii^esiècle fondateur desthéorèmes de convergence.Une loi binomiale peut également être utilisée pour modéliser des situations simples de succès ou échec, un jeu depile ou facepar exemple. Le calcul de safonction de massedevient rapidement fastidieux lorsquenest grand, il est alors possible d'utiliser des approximations par d'autreslois de probabilitételles que laloi de Poissonou laloi normaleet d'utiliser des tables de valeurs.

La loi binomiale est utilisée dans divers domaines d'étude, notamment à travers destests statistiquesqui permettent d'interpréter des données et de prendre des décisions dans des situations dépendant de l'aléa. De par la simplicité de sa définition, c'est l'une des lois de probabilité étudiées dans les cours d'introduction à la théorie des probabilités.

Explication intuitive

Pile ou face.

Premiers exemples

Pile ou face

Considéronsnlancers successifs d'une pièce de monnaie. Alors le nombre de fois où la pièce apparaît du côté pile suit la loi binomiale où le nombre d'expériences réalisées estnet où la probabilité de succès est$p={\frac {1}{2}}$.

Lancer de dé

Considéronsnlancers successifs d'un dé à 6 faces. Alors le nombre de fois où l'on obtient un 1, suit la loi binomiale où le nombre d'expériences réalisées estnet où la probabilité de succès est$p={\frac {1}{6}}$.

Définition intuitive

Uneloi de Bernoullidécrit le comportement d'uneexpérience aléatoirequi possède deux résultats possibles traditionnellement appelés succès et échec.Une telle expérience s'appelle uneépreuve de Bernoulli.Par exemple, lors d'un lancer depile ou face,on peut considérer qu'obtenir face est un succès et obtenir pile est un échec. Dans ce modèle, la probabilité de succès est une valeur fixe, c'est-à-dire qui reste constante à chaque renouvellement de l'expérience aléatoire. Cette probabilité de succès est notéep.Nous pouvons noter sa loi de probabilité:

$x\in \{0;1\},\;\;\;\mathbb {P} (X=x)=p^{x}(1-p)^{1-x}$

On considère la situation où une telle expérience aléatoire (deux résultats possibles et une probabilité fixe) est répétée un certain nombre de fois de manière indépendante; notonsnce nombre de fois. Cette répétition indépendante d'épreuves de Bernoulli s'appelle unschéma de Bernoulliou simplement desépreuves de Bernoulli.Une loi binomiale décrit le nombre de fois où lesuccèsapparaît sur lesnexpériences effectuées. Le nombre de succès obtenus étant une valeur aléatoire, une loi binomiale est décrite grâce à la donnée des probabilités que le succès apparaisse précisémentkfois sur lesnessais.

Arbre de probabilité

Arbre de probabilitépour une loi binomiale associée à 3 épreuves de Bernoulli.

Une manière visuelle de représenter une suite d'expériences est d'utiliser unarbre de probabilité.Chaque épreuve est représentée par deux branches: l'une pour le succès, l'autre l'échec. À chaque extrémité, on rajoute deux branches (succès et échec) pour l'épreuve suivante. On recommence jusqu'au nombre total d'épreuves. À chaque extrémité finale, on peut compter le nombre de succès obtenus. Il suffit de multiplier le nombre de fois où il y aksuccès par la probabilité d'obtenirksuccès pour obtenir la probabilité correspondante de la loi binomiale.

Par exemple, on lance 3 fois de suite un dé équilibré à six faces et on s'intéresse au nombre de fois que le1apparaît. Il apparaît 0, 1, 2 ou 3 fois. Chaque lancer est indépendant des autres et la probabilité d'obtenir le1est de1/6sur chacun d'entre eux, autrement dit la probabilité qu'il n'apparaisse pas est de5/6à chaque lancer. Ainsi, pour chaque lancer, on considère une loi de Bernoulli de paramètre1/6.Il y a trois configurations pour obtenir une seule fois le1:il apparaît au premier lancer ou au deuxième ou au troisième. Chacune de ces issues a la même probabilité d'apparaître:${\frac {1}{6}}\times {\frac {5}{6}}\times {\frac {5}{6}}$.La probabilité pour avoir une fois le1est alors:$3\times {\frac {1}{6}}\times {\frac {5}{6}}\times {\frac {5}{6}}$.On retrouve bien$\mathbb {P} (X=1)={3 \choose 1}\left(1/6\right)^{1}\left(5/6\right)^{3-1}$pour une loi binomialeb(3, 1/6).Il est possible de retrouver les autres probabilités de la même façon.

Définition mathématique

Laloi binomialeest uneloi de probabilité discrèteà deux paramètres:$n\in \mathbb {N} ^{*}$et$p\in [0;1]$.Il est fréquent d'utiliser également le paramètreq= 1 –ppour avoir des expressions plus concises. Elle possède plusieurs définitions équivalentes:

Diagrammes en bâtonsde trois fonctions de masse de lois binomiales. Les paramètres sontn= 20etp= 0,1(en bleu),p= 0,5(en vert) etp= 0,8(en rouge).

Définition 1—La loi binomiale, de paramètresnetp,est laloi de probabilitéd'une variable aléatoireXégale au nombre de succès rencontrés au cours d'une répétition denépreuves de Bernoulli,pétant la probabilité desuccèsdans chacune d'entre elles.

Définition 2—La loi binomiale, de paramètresnetp,est laloi de probabilitéd'une variable aléatoireXtelle que:

$X=Y_{1}+Y_{2}+\dots +Y_{n},$

où$Y_{1},Y_{2},\dots,Y_{n},$sont desvariables aléatoires indépendantesdeloi de Bernoullide même paramètrep.

Définition 3—La loi binomiale, de paramètresnetp,est laloi de probabilité discrèted'une variable aléatoireXdont lafonction de masseest donnée par:

$\mathbb {P} (X=k)={n \choose k}p^{k}q^{n-k}$pour$k=0,1\dots,n$.

On rappelle que des variables aléatoires$Y_{1}$et$Y_{2}$de loi discrète sontindépendantessi$\mathbb {P} (Y_{1}=k,Y_{2}=h)=\mathbb {P} (Y_{1}=k)\mathbb {P} (Y_{2}=h)$.

La fonction de masse donnée dans la définition 3 a bien un sens puisque laformule du binôme de Newtondonne:$\sum _{k=0}^{n}\mathbb {P} (X=k)=\sum _{k=0}^{n}{n \choose k}p^{k}q^{n-k}=(p+1-p)^{n}=1$.La définition 2 est l'écriture mathématique de la définition 1.

La définition 3 est équivalente aux deux autres: on calcule explicitement la probabilité queksuccès apparaissent dansnessais. Puisque lesnrépétitions sont indépendantes, la probabilité d'obtenirksuccès et doncn – kéchecs est:$p^{k}(1-p)^{n-k}$,dans le cas où on ne tient pas compte de la place des résultats.Il suffit alors de s'intéresser à la place desksuccès etn – kéchecs. C'est-à-dire, combien y a-t-il de manière de placerksuccès parminrésultats (sans s'occuper de l'ordre entre les succès)? C'est le nombre decombinaisonsdekéléments parminélémentsdonné par lecoefficient binomial${n \choose k}$.On retrouve alors la fonction de masse de la définition 3.

Notation

Le fait qu'une variable aléatoireXsuive une loi binomiale de paramètresnetpest noté:$X\sim b(n,p)$;$X\sim B(n,p)$ou$X\sim Bi(n,p)$.

Mesure de probabilité

Puisque la loi binomialeb(n,p)est une loi discrète, il est possible de la définir grâce à samesure de probabilité:

$\mathbb {P} =\sum _{k=0}^{n}{n \choose k}p^{k}q^{n-k}\delta _{k}$,où$\delta _{k}$est lamesure de Diracau pointk.

Historique

Laplanche de Galton:les billes rouges (les points rouges sur la figure) empilées dans le bas de l'appareil correspondent à lafonction de massede la loi binomiale, la courbe bleue correspond à la densité de la loi normale.

La loi binomiale fait partie des plus anciennes lois de probabilités étudiées.Elle a été introduite parJacques Bernoulliqui y fait référence en 1713 dans son ouvrageArs Conjectandi.Entre 1708 et 1718, on découvre aussi laloi multinomiale(généralisation multi-dimensionnelle de la loi binomiale), laloi binomiale négativeainsi que l'approximation de la loi binomiale par laloi de Poisson,laloi des grands nombrespour la loi binomiale et une approximation de laqueuede la loi binomiale.

Grâce à l'expression de safonction de masse,la loi binomiale a été utilisée par plusieurs scientifiques pour réaliser des calculs dans des situations concrètes. C'est le cas d'Abraham de Moivrequi réussit à trouver une approximation de la loi binomiale par laloi normale,il publie d'abord ses résultats en 1733 en latin:Approximatio ad summam terminorum binomii(a + b)ⁿin seriem expansi,puis les traduit pour les publier en 1738 dansThe Doctrine of Chances(en).En 1812,Pierre-Simon de Laplacereprend ces travaux.Francis Galtoncrée laplanche de Galtonqui permet d'avoir une représentation physique de cette convergence.En 1909,Émile Borelénonce et prouve, dans le cas de la loi binomiale, la première version de laloi forte des grands nombres.

Plus récemment, en 1914,McKendrickdémontre que la loi binomiale est la solution d'un processus simplede naissance et d'émigration.D'après les travaux deWilliam Felleren 1957, elle peut aussi être vue comme laloi stationnairepour lemodèle des urnes d'Ehrenfest.Cette même année, Haight montre que la loi binomiale est liée à unproblème de file d'attente.

La loi binomiale apparaît dans de nombreuses applications auXX^esiècle:engénétique,enbiologie animale,enécologie végétale,pour lestests statistiques,dans différents modèles physiques tels que des réseaux téléphoniquesou le modèle des urnes d'Ehrenfest, etc.

Le nom « binomiale » de cette loi provientde l'écriture de sa fonction de masse (voir ci-dessous) qui contient uncoefficient binomialissu du développement du binôme:(p + q)ⁿ.

Représentation sous la forme d'un arbre

Représentation de la loi binomiale sous forme d'un arbre.

Puisque la loi binomiale est une suite d'épreuves de Bernoulli, il est possible de la représenter grâce à unarbre de probabilité:chaque nœud représente le résultat d'une épreuve, les probabilités de succès et d'échecs sont représentés par deux branches distinctes rattachées à un nœud. Le graphique est donc unarbre binaireéquilibré. Un arbre contenantngénérations correspond à une loi binomialeb(n,p).

Si on indique les résultats de chaque épreuve sur les arêtes de l'arbre, il est possible de visualiser les différentes issues de la loi binomiale.Si ce sont les valeurs des probabilités qui sont indiquées sur les arêtes, alors les probabilités de la loi binomiale apparaissent au bout des branches(voir le graphique ci-contre).

Le graphique est un arbre de probabilité pour une loi binomiale de paramètren= 3.Sur chaque branche sont indiquées les probabilités des différentes issues: par exemple branches droite, gauche puis droite; c'est-à-dire échec, succès puis échec. Au bout des branches de l'arbre, apparaissent les probabilités de chaque issue de la loi binomialeb(3,p).C'est-à-dire pour les valeursk= 0, 1, 2ou3,on obtient$\mathbb {P} (X=0)=q^{3}$,$\mathbb {P} (X=1)=3pq^{2}$,$\mathbb {P} (X=2)=3qp^{2}$et$\mathbb {P} (X=3)=p^{3}$.On retrouve ainsi les différentscoefficients binomiaux:${3 \choose 0}=1{\text{; }}{3 \choose 1}=3{\text{; }}{3 \choose 2}=3{\text{; }}{3 \choose 3}=1{\text{.}}$

Propriétés

Moments

Les plus connus sont l'espéranceet lavariance,que l'on déduit classiquementde ladéfinition 2 ci-dessus:

$\mathbb {E} (X)=np\quad {\text{et}}\quad \operatorname {Var} (X)=npq$.

Lesmoments factorielsde la loi binomiale de paramètresnetpsont:

$\mathbb {E} \left((X)_{k}\right)=\mathbb {E} \left(X(X-1)...(X-k+1)\right)={\frac {n!}{(n-k)!}}~p^{k}$.

Par conséquent,sesmoments ordinairessont:

$\mu '_{r}=\mathbb {E} (X^{r})=\sum _{k=0}^{r}{\frac {n!}{(n-k)!}}$S(r,k)p^k, avec comme premières valeurs:

$\mu '_{1}=\mathbb {E} (X)=$	$np$(espérance)
$\mu '_{2}=\mathbb {E} (X^{2})=$	$np+n(n-1)p^{2}$
$\mu '_{3}=\mathbb {E} (X^{3})=$	$np+3n(n-1)p^{2}+n(n-1)(n-2)p^{3}$

On peut aussi les obtenir par laformule de récurrence

$\mu '_{r+1}=pq\left({\frac {n}{q}}\mu '_{r}+{\frac {{\rm {d}}\mu '_{r}}{{\rm {d}}p}}\right)$,

où le terme${\frac {\rm {d}}{{\rm {d}}p}}$désigne ladérivéepar rapport à la variablep.

Les moments inverses, c'est-à-dire$\mathbb {E} (X^{-r})$avec$r\in \mathbb {N} ^{*}$,sont infinis.

Moments centrés

Lesmoments centréssont les moments de la différence entre la variable et sa moyenne.

$\mu _{2}=Var(X)=\mathbb {E} \left((X-np)^{2}\right)=$	$npq\;$;(variance)
$\mu _{3}=\mathbb {E} \left((X-np)^{3}\right)=$	$np(1-p)(1-2p)=npq(q-p)$
$\mu _{r}=\mathbb {E} ((X-np)^{r})=$	$npq\sum _{k=0}^{r-2}{r-1 \choose k}\mu _{k}-p\sum _{k=0}^{r-2}{r-1 \choose k}\mu _{k+1}$

L'expression de la variance donne l'écart type:$\sigma {(X)}={\sqrt {npq}}$.

Les moments centrés se calculent aussi par cette autre relation de récurrence:

$\mu _{r+1}=pq\left(nr\mu _{r-1}+{\frac {{\rm {d}}\mu _{r}}{{\rm {d}}p}}\right)$.

Écart moyen

L'Écart moyen(ou déviation moyenne) est la moyenne des écarts à la moyenne; il est donné par:

$\mathbb {E} (|X-np|)=2n{n-1 \choose \lfloor np\rfloor }p^{\lfloor np\rfloor +1}q^{n-\lfloor np\rfloor }$,

où$\lfloor np\rfloor$est lapartie entièredenp.

Par exemple, si$X\sim B(2n,1/2)$,$\mathbb {E} (|X-n|)=n{\frac {2n \choose n}{2^{2n}}}\sim {\sqrt {n \over \pi }}$,valeur à comparer avec l'écart-type:${\sqrt {\mathbb {E} ((X-n)^{2})}}={\sqrt {n \over 2}}$.

Fréquence de succès

Grâce aux formules précédentes, on obtient les moments de la fréquence des succès:${\frac {X}{n}}$:

moment d'ordre1(ou espérance) de la fréquence de succès	$\mathbb {E} \left[{\frac {X}{n}}\right]=$	$p$
moment centré d'ordre2(ou variance) de la fréquence de succès	$\mathbb {E} \left[\left({\frac {X}{n}}-p\right)^{2}\right]=$	${\frac {p(1-p)}{n}}={\frac {pq}{n}}$
moment centré d'ordre4de la fréquence de succès	$\mathbb {E} \left[\left({\frac {X}{n}}-p\right)^{4}\right]=$	${\frac {pq(1-6pq)}{n^{3}}}+3{\frac {p^{2}q^{2}}{n^{2}}}$

L'expression de la variance de la fréquence donne l'écart type de la fréquence des succès:$\sigma _{X/n}={\sqrt {\frac {p(1-p)}{n}}}={\frac {\sqrt {pq}}{\sqrt {n}}}$.

Covariance

On considère deux variables aléatoires$X_{1}$et$X_{2}$,pas forcémentindépendantes,de lois binomiales respectives$b(n,p_{1})$et$b(n,p_{2})$.Lacovariancepermet d'évaluer la dépendance entre les deux variables:

$\mathrm {Cov} (X_{1},X_{2})=n\mathbb {P} (X_{1}=1{\text{ et }}X_{2}=1)-np_{1}p_{2}$.

Propriétés et caractérisations

Valeurs descriptives de la loi

• Lecoefficient d'asymétried'une loi binomialeb(n,p)est:$\gamma ={\frac {q-p}{\sqrt {npq}}}$.L'asymétriede la loi binomialeb(n,p)est positivesip< 1/2et négative sip> 1/2.La loi est symétrique si et seulement sip= 1/2.
• Lamédianede la loi binomiale est$m=\lfloor np\rfloor$ou$m=\lfloor np\rfloor +1$,le signe$\lfloor.\rfloor$désigne lapartie entière.Ces valeurs s'obtiennent grâce à la formule:$|m-np|<\ln(2)$(cette borne étant optimale).
• Lemodede la loi binomialeb(n,p)est la valeur$\lfloor (n+1)p\rfloor$,elle est la valeur de plus grande probabilité.

Sinpest unentier,alors le mode, la moyenne et la médiane valent tous troisnp.

Propriétés de stabilité

• SiXsuit une loi binomialeb(n,p),alorsY = n – Xsuit une loib(n,1 –p).Cette symétrie donne les relations suivantes pour la fonction de répartition et pour la fonction de masse:$\mathbb {P} (X\leq k)=\mathbb {P} (Y\geq n-k)$et$\mathbb {P} (X=k)=\mathbb {P} (Y=n-k)$.
• Si lesvariables aléatoiresindépendantes$X_{1}$et$X_{2}$sont de lois binomiales respectives$b(n_{1},p)$et$b(n_{2},p)$,alors la variable aléatoire$X_{1}+X_{2}$est de loi binomiale$b(n_{1}+n_{2},p)$.Cette propriété peut s'obtenir grâce à l'expression des fonctions caractéristiques ou grâce à l'écriture sous forme de somme de variables de Bernoulli.

Inégalités

• L'inégalité de Bienaymé-Tchebychevpour une variable aléatoireXsuivant la loi binomialeb(n,p)est obtenue grâce aux moments:

  $\mathbb {P} \left(\left|{\frac {X}{n}}-p\right|>x\right)\leq {\frac {p(1-p)}{nx^{2}}}$.

• L'inégalité de Hoeffdingpour une variable aléatoireXde loib(n,p)est plus précise que l'inégalité de Bienaymé-Tchebychev lorsquexest grand, elle s'écrit:

  $\mathbb {P} \left(\left|{\frac {X}{n}}-p\right|>x\right)\leq 2\mathrm {e} ^{-2nx^{2}}$.

• L'inégalité de Kolmogorovs'écrit pour une somme de variables aléatoires indépendantes. Pour des variables aléatoires indépendantes$X_{1},X_{2}\dots,X_{n}$deloi de Bernoulli,la somme$Y_{k}=\sum _{i=1}^{k}X_{i}-kn$suit une loi binomialeb(k,p)recentrée, l'inegalité s'écrit alors:

  $\mathbb {P} \left(\sup \left(\left|Y_{k}\right|\,;\,k=1,\dots,n\right)>\varepsilon \right)\leq {\frac {np(1-p)}{\varepsilon ^{2}}}$.

Caractérisations

• En 1964, un cas particulier d'un théorème de Patil et Seshadri énonce:si laloi conditionnelledeX + YsachantXest uneloi hypergéométriquede paramètresmetn,alorsXetYsuivent des lois binomiales de paramètres respectifs$(m,\theta )$et$(n,\theta )$où$\theta$est arbitraire.
• En 1973, Kagan, Linnik et Rao donnent plusieurs caractérisations en considérant desmarches aléatoiresà pas binomiaux sur un réseau avec destemps d'arrêt markoviens.
• En 1991, Ahmed démontre qu'une variable aléatoireXsuit une loi binomiale variable aléatoireb(n,p)si et seulement si$\mathbb {E} (X|X>k)=np+qkh_{k}$où$h_{k}=\mathbb {P} (X=k)/\sum _{i=k}^{n}p_{i}$.

Fonction de répartition

Graphique de 3 fonctions de répartition de lois binomiales avec paramètres:n= 20etp= 0,1(en bleu),p= 0,5(en vert) etp= 0,8(en rouge).

Lafonction de répartitiond'une variable aléatoireXsuivant la loi binomialeb(n,p)est donnée par:

$F(x)=\mathbb {P} (X\leq x)={\begin{cases}1&{\textrm {si}}\;x\geq n\\[4pt]\displaystyle \sum _{k=0}^{\lfloor x\rfloor }{n \choose k}p^{k}(1-p)^{n-k}&{\textrm {si}}\;0\leq x<n\\[4pt]0&{\textrm {si}}\;x<0\end{cases}}$

où$\lfloor x\rfloor$est lapartie entièredex.

Même s'il existe une expression de la fonction de répartition, son calcul n'est pas facileà cause des coefficients binomiaux${n \choose k}$,notamment lorsquenest grand. Il existe alors des tables de valeurs (voirci-dessous). Des théorèmes d'approximation ont été développéspour approcher de manière théorique et calculatoire cette fonction de répartition (voirci-dessous). L'expression suivante provient du lien entre la loi binomiale et laloi bêta(voirci-dessous): pour$0\leq x<n$

$F(x)={\frac {1}{\mathrm {B} \left(\lfloor x\rfloor +1,n-\lfloor x\rfloor \right)}}\int _{p}^{1}t^{\lfloor x\rfloor }(1-t)^{n-\lfloor x\rfloor -1}{\rm {d}}t$

oùBest lafonction bêta. il est alors possible d'écrire la fonction de répartition grâce à lafonction bêta incomplète:

$F(x)=I_{1-p}(n-\lfloor x\rfloor,1+\lfloor x\rfloor )$.

Fonctions caractéristique et génératrice

Lafonction caractéristiqued'une variable aléatoireXsuivant la loi binomialeb(n,p)est donnée par:

$\phi (t)=\mathbb {E} \left(\mathrm {e} ^{\mathrm {i} tX}\right)=\left(q+p\mathrm {e} ^{\mathrm {i} t}\right)^{n}\;,\;\forall t\in \mathbb {R}$.

Lafonction génératrice des momentsd'une variable aléatoireXsuivant la loi binomialeb(n,p)est donnée par:

$M(t)=\mathbb {E} \left(\mathrm {e} ^{tX}\right)=\left(q+p\mathrm {e} ^{t}\right)^{n}\;,\;\forall t\in \mathbb {R}$.

On déduit directement lafonction génératrice des cumulants:

$\ln(M(t))=n\ln \left(q+p\mathrm {e} ^{t}\right)\;,\;\forall t\in \mathbb {R}$,

et lafonction génératrice des cumulants factoriels:

$\ln \left(\mathbb {E} \left[(1+t)^{X}\right]\right)=n\ln \left(1+pt\right)\;,\;\forall t\in \mathbb {R} _{+}$.

Lien avec d'autres lois

Loi de Bernoulli

Rappelons que la loi binomiale de paramètres$n\in \mathbb {N} ^{*}$et$p\in [0,1]$est la loi de la somme denvariables aléatoires indépendantes deloi de Bernoullide même paramètrep.

Ainsi, la loi binomialeb(1,p)est une loi de Bernoulli de paramètrep.

C'est par cette représentation du nombre de succès et d'échecs dans une suite d'épreuves que la loi binomiale est source de nombreuses applications.

Lois réciproques

Les lois suivantes ont un lien avec la loi binomiale grâce à leur fonctions de répartition. Lorsque le nombre de succèskest fixé, elles donnent la loi du nombre d'épreuves nécessaires (loi binomiale négative) ou la loi du paramètrep(lois bêta ou de Fisher). En ce sens, elles peuvent servir delois réciproques.

• La loi binomialeb(n,p)donne le nombre de succès dans une succession denépreuves indépendantes. Laloi binomiale négative,ou loi de Pascal,$Pa(k,p)$est le nombre d'épreuves nécessaires pour obtenirksuccès.le termenégatifprovient de l'écriture de la fonction de masse qui contient un coefficient binomial avec un terme négatif.
  De plus, siXsuit une loi$Pa(k,p)$et siYsuit une loib(n + k,p)alors,pourkentre0etn:
  $\mathbb {P} (Y\leq k)=1-I_{p}(k,n+1)=\mathbb {P} (X\geq n)$,où$I_{p}$est lafonction bêta incomplète.Autrement dit: la probabilité qu'il faille au moinsnépreuves pour avoirksuccès est égale à la probabilité qu'il y ait au plusksuccès enn + képreuves.
• Grâce au calcul de la fonction de répartition de laloi bêtadonnée par lafonction bêta incomplète$I_{p}$,on obtient,pourkentre0etn:

$\mathbb {P} (Y\leq k)=1-I_{p}(k+1,n-k)=\mathbb {P} (X\geq p)$oùXsuit une loi bêta de paramètresk+ 1,n – ketYsuit une loi binomialeb(n,p).

• La loi binomiale est liée à laloi de Fisherpar la propriété suivante:siYsuit une loi binomialeb(n,p)alors, pourkentre0etn:

$\mathbb {P} (Y\leq k)=\mathbb {P} (F>{\frac {\nu _{2}}{\nu _{1}}}\cdot {\frac {p}{1-p}})$oùFsuit une loi de Fischer de paramètres$\nu _{1}=2(k+1)\,,\,\nu _{2}=2(n-k)$.

La relation précédente permet de trouver lesquantilesde la loi binomiale.

Autres lois

• Laloi binomiale (doublement) tronquéede paramètres$n,p,r_{1}$et$r_{2}$est la loi binomialeb(n,p)avec$r_{1}<n-r_{2}$telle que les valeurs dans$[0,r_{1}[$et dans$]n-r_{2},n]$sont enlevées.Lafonction de massede cette loi est donnée par l'expression: pour$k=r_{1},\dots,n-r_{2}$

$\mathbb {P} (X=k)={n \choose k}p^{k}q^{n-k}/\sum _{i=r_{1}}^{n-r_{2}}{n \choose i}p^{i}q^{n-i}.$

De la même manière, il est possible de définir la loi binomiale (simplement) tronquéeen omettant uniquement les valeurs entre0et$r_{1}$ou entre$n-r_{2}$et$n$.

• Laloi binomiale positiveouloi binomiale tronquée en 0est la loi binomialeb(n,p)dont on retire la valeur 0. Sa fonction de masse est:$\mathbb {P} (X=k)={n \choose k}{\frac {p^{k}q^{n-k}}{1-q^{n}}}$.De la même manière il est possible de définir laloi binomiale négative.
• Laloi multinomialeest la généralisation multi-dimensionnelle de la loi binomialedans le sens où la loi multinomiale modélise une succession d'épreuves dont chacune possède plusieurs issues, pas uniquement succès ou échec. Cette loi multidimensionnelle donne les probabilités du nombre d'apparition des différentes issues dans une succession d'épreuves indépendantes.
• Laloi bêta-binomialeest construite grâce à un mélange de loi:une variable aléatoire qui suit une loi binomiale$b(n,\pi )$dont le paramètre$\pi$est une variable aléatoire qui suit uneloi bêta$B(\alpha,\beta )$,est de loi bêta-binomiale de paramètres$n,\alpha,\beta$.Cette loi binomiale est similaire à laloi hypergéométrique négative(en),il suffit de changer les paramètres.
• La fonction de masse d'une variableYdeloi hypergéométriquede paramètres$A,p=1-q,n$est donnée par:$\mathbb {P} (Y=k)={\frac {{k \choose pA}{n-A \choose qA}}{n \choose A}}$.Elle correspond au nombre tirages gagnants dans une expérience dentirages simultanés dans une urne contenantAboules et une proportion depboules gagnantes.

Si le nombre de boules augmente, c'est-à-direAtend vers l'infini, et sip/Atend vers une valeur$p'\in [0,1]$,alors la loi hypergéométrique converge vers une loi binomialeb(n,p').

Autrement dit, si la taille de la population (A) est grande par rapport à la taille de l'échantillon (n), alors les tirages peuvent être convenablement représentés par une loi binomiale de paramètrep'égal au pourcentage (p) d'éléments ayant le caractère étudié.

De plus, si$X_{1}$et$X_{2}$sont deux variables aléatoires indépendantes de loi binomiale respectives$b(n_{1},p)$et$b(n_{2},p)$,alors la loi de$X_{1}$sachant que$X_{1}+X_{2}=k$est la loi hypergéométrique de paramètres:$k,{\frac {n_{1}}{n_{1}+n_{2}}}$et$n_{1}+n_{2}$.

Convergences et approximations

Pour de grandes valeurs den,le calcul des fonctions de masse et de répartition deviennent vite fastidieux. Une méthode est d'approcher ces valeurs grâce aux théorèmes limites. La loi (faible ou forte) des grands nombres permet d'approcher la moyenne de la loi binomiale. Pour obtenir des valeurs approchées de la fonction de répartition, il est possible d'utiliser l'approximation normale ou l'approximation par laloi de Poisson.L'approximation normale est plus performante lorsque le paramètrepn'est pas trop proche de0ou de1,sinon l'approximation par la loi de Poisson donne de meilleurs résultats.

Loi des grands nombres

Laloi faible des grands nombres,appliquée à unprocessus de Bernoullide paramètrep,garantit que pour toute suite(X_n)de variables aléatoires, définies sur un mêmeespace probabilisé,et de lois respectivesb(n,p)(cf. définition 2ci-dessus), on a, pour tout$\varepsilon >0$: $\lim _{n\to +\infty }\mathbb {P} \left(\left|{\frac {X_{n}}{n}}-p\right|<\varepsilon \right)=1.$ Plus précisément, puisque l'espérance et la variance deX_nsont respectivement égales ànpetnp(1 –p),l'inégalité de Bienaymé-Tchebychevmontre que: $\mathbb {P} \left(\left|{\frac {X_{n}}{n}}-p\right|>\varepsilon \right)<{\frac {p(1-p)}{n\,\varepsilon ^{2}}}.$ Cela peut s'interpréter grossièrement de la manière suivante. Si l'on sait que lors d'une expérience aléatoire (tirage d'un individu dans une population de grande taille, lancer d'une pièce…) la probabilité d'apparition de la propriétéAestp(A),alors la fréquence d'apparition de la propriétéAau cours denexpériences de ce type (tirages denindividus dans une population de taille très supérieure àn,nlancers de pièce…) est souvent voisine dep(A),avec une probabilité d'autant meilleure quenest grand et quep(A)est proche de0ou1.

Il existe de meilleures majorations de cette probabilité, l'inégalité de Hoeffdingdonne: $\mathbb {P} \left({\frac {X_{n}}{n}}-p>\varepsilon \right)<\mathrm {e} ^{-2n\varepsilon ^{2}}.$

Convergence vers la loi de Poisson

Convergence

Considérons une loi binomialeb(n,p)telle que les paramètresnetpsont liés par la formule:$np=\lambda >0$où$\lambda$est fixé. Lorsquentend vers l'infini, et doncptend vers 0, alors:$\lim _{n\rightarrow +\infty }{n \choose k}p^{k}q^{n-k}=\mathrm {e} ^{-\lambda }{\frac {\lambda ^{k}}{k!}}$.Autrement dit, la probabilité qu'une variable de loi binomiale prenne la valeurkconverge (lorsquendevient grand) vers la probabilité qu'une variable deloi de Poissonprenne la valeurk.Le paramètrepconverge alors vers 0, il correspond donc à un évènement de probabilité très faible, la loi de Poisson est alors appelée loi des évènements rares.Par sommation, on obtient alors le résultat:

$\lim _{n\rightarrow +\infty }\mathbb {P} (X\leq x)=\lim _{n\rightarrow +\infty }\sum _{k=0}^{\lfloor x\rfloor }{n \choose k}p^{k}q^{n-k}=\mathrm {e} ^{-\lambda }\sum _{k=0}^{\lfloor x\rfloor }{\frac {\lambda ^{k}}{k!}}=\mathbb {P} (Y\leq x)$

où$\lfloor \cdot \rfloor$est la partie entière,Xest une variable de loi binomiale etYde loi de Poisson${\mathcal {P}}(\lambda )$.Cette limite montre laconvergence en loide la loi binomiale (avec les conditions précédentes) vers la loi de Poisson. Une expression plus détaillée de la convergence peut être donnée par la formule:$\mathbb {P} (X\leq x)=\mathrm {e} ^{-\lambda }\sum _{k=0}^{\lfloor x\rfloor }{\frac {\lambda ^{k}}{k!}}+{\mathcal {O}}\left({\frac {1}{n^{2}}}\right)$avec$\lambda ={\frac {(2n-\lfloor x\rfloor )p}{2-p}}$lorsquentend vers l'infini et${\mathcal {O}}(\cdot )$est lecomparateur asymptotique.

Fonctions de masse d'une loi binomiale$b(24\,;\,0,5)$(en violet),$b(60\,;\,0,2)$(en rouge) et d'une loi de poisson${\mathcal {P}}(12)$(en bleu).

En 1953,Iouri Prokhorovdonne une majoration de l'erreur totale d'approximation entre la fonction de répartition d'une loi binomialeb(n,p)et uneloi de Poisson${\mathcal {P}}(np)$:$\sum _{k=0}^{+\infty }\left|{n \choose k}p^{k}q^{n-k}-{\frac {\mathrm {e} ^{-np}(np)^{k}}{k!}}\right|\leq \min(2np^{2},3p)$.Il est également possible de borner le ratio entre les deux fonctions de répartition:$\mathrm {e} ^{np}\left(1-{\frac {k}{n}}\right)^{k}q^{n}\leq {\frac {{n \choose k}p^{k}q^{n-k}}{\mathrm {e} ^{-np}(np)^{k}/k!}}\leq \mathrm {e} ^{np}q^{n-k}.$

Approximation

Grâce à la convergence ci-dessus, il est possible d'approcher les probabilités de la loi binomiale par la loi de Poisson. En pratique, le cas s'applique lorsquenest grand et doncppetit. Différentes valeurs sont proposées:

• $p<0,4$,lorsque$n=3$(ce qui fait$np<1,2$);
• $p<0,3$,lorsque$n=30$(ce qui fait$np<9$);
• $p<0,2$,lorsque$n=300$(ce qui fait$np<60$);
• $0<np<10$;
• $p<0,1$,lorsque$n\geq 30$;
• $np\leq 10$et$n\geq 1500p$.

L'idée commune de toutes ces propositions est d'avoir la valeurnpstable lorsquenest grand etppetit.

Convergence vers la loi normale

Illustration de la convergence de la fonction de masse de la loi binomiale vers la loi normale lorsquengrandit.

Convergence

Le théorème de Moivre-Laplace, énoncé en 1733, montre qu'une variable aléatoire de loi binomiale, convenablement renormalisée,converge en loivers une variable aléatoire deloi normale.Ce résultat peut s'énoncer grâce aux fonctions de répartition des deux lois. Considérons une variable aléatoireXde loi binomialeb(n,p),la variable aléatoireXrenormalisée est la variable aléatoire centrée et réduite, c'est-à-dire:${\frac {X-\mathbb {E} (X)}{\sigma _{X}}}={\frac {X-np}{\sqrt {npq}}}$. Si l'on note$\Phi$la fonction de répartition de la loi normale, alors:

Théorème de Moivre-Laplace:pour tout$x\in \mathbb {R}$,$\lim _{n\to +\infty }\mathbb {P} \left({\frac {X-np}{\sqrt {npq}}}\leq x\right)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}\mathrm {e} ^{-{\frac {t^{2}}{2}}}{\rm {d}}t=\Phi (x).$

Bien qu'Abraham de Moivren'ait énoncé ce résultat que dans le cas d'une loi binomiale,cette convergence est généralisée dans le cas d'autres lois, c'est lethéorème central limite.Ce théorème permet d'approcher une loi discrète par une loi continue, il est alors utile d'ajouter un coefficient, ditcorrection de continuité,afin d'améliorer les approximations futures (voir ci-dessous). La convergence précédente peut alors s'écrire sous forme d'équivalencelorsquentend vers l'infini:pour tout$a,b\in \mathbb {R}$

$\mathbb {P} \left(a\leq X\leq b\right)\approx \mathbb {P} \left({\frac {a-{\frac {1}{2}}-np}{\sqrt {npq}}}\leq {\frac {X-np}{\sqrt {npq}}}\leq {\frac {b+{\frac {1}{2}}-np}{\sqrt {npq}}}\right)\operatorname {\sim } _{n\rightarrow +\infty }\Phi \left({\frac {b+{\frac {1}{2}}-np}{\sqrt {npq}}}\right)-\Phi \left({\frac {a-{\frac {1}{2}}-np}{\sqrt {npq}}}\right).$

L'erreur commise par l'approximation est estimée par l'inégalité de Berry-Esseendont la constante est régulièrement améliorée, elle fournit une borne de la différence entre les deux fonctions de répartition lorsquenest grand,pourXune variable aléatoire de loi binomialeb(n,p)etYde loi normale${\mathcal {N}}(0,1)$de fonction de répartition notée$\Phi$:$\sup _{x\in \mathbb {R} }\left|\mathbb {P} \left({\frac {X-np}{\sqrt {npq}}}\leq x\right)-\Phi (x)\right|\leq {\frac {0,4748}{\sqrt {npq}}}$.Une expression plus détaillée de la convergence peut être donnée par la formule avec correction de continuité:$\mathbb {P} (X\leq x)=\Phi \left({\frac {x-np+1/2}{\sqrt {npq}}}\right)+{\mathcal {O}}({\frac {1}{\sqrt {n}}})$uniformémentpour toute variablex,lorsquentend vers l'infini et où${\mathcal {O}}(\cdot )$est lecomparateur asymptotique.D'autres approximations plus fines ont été étudiées,par exemple parLaplace(1820),Prokhorov(1953) ouPeizeretPratt(en)(1968).

Approximation

Grâce aux théorèmes de convergence ci-dessus, lorsquenest grand, les probabilités de la binomiale renormalisée peuvent être approchées par les valeurs des probabilités de la loi normale. Il existe plusieurs règles sur les paramètresnetppour que l'approximation soit valable:

• $n>30$,$np>5$et$nq>5$;
• $npq>9$ou$npq>18$;
• $np>9$et$p<1/2$.

L'influence de ces paramètres sur l'approximation a été finement étudiée dans les années 1990, par exemple:pournfixé, l'erreur absolue minimale est atteinte pourp= 1/2;l'erreur absolue est inférieure à$0,0212/{\sqrt {npq}}$.

Tables de la loi binomiale

Des tables de lafonction de masseet de lafonction de répartitionde la loi binomiale ont été publiées en 1950 par leNational Bureau of Standardspuis en 1955 dansNational of the Computation Laboratoryet par Raoet al.en 1985.

Grâce aux relations de symétrie (voirci-dessus), il suffitde donner des tables de valeurs pour$p\leq 0{,}5$.

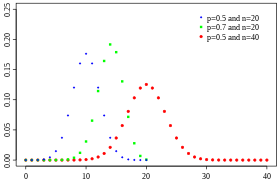
Valeurs de la fonction de masse

Les tables de valeurs suivantesdonnent les valeurs de la fonction de masse de la loi binomialeb(n,p)pour différentes valeurs den.

Exemples: SiXsuit une loi$b(10\,;\,0,15)$,alors$\mathbb {P} (X=4)\simeq 0,0401$.SiYsuit une loi$b(10\,;\,0,85)$,alors$\mathbb {P} (Y=4)=\mathbb {P} (X=6)\simeq 0,0012$.

Pourn= 5

$k/p$	0,05	0,10	0,15	0,20	0,25	0,30	0,35	0,40	0,50
0	0,7738	0,5905	0,4437	0,3277	0,2373	0,1681	0,1160	0,0778	0,0312
1	0,2036	0,3281	0,3915	0,4096	0,3955	0,3601	0,3124	0,2592	0,1562
2	0,0214	0,0729	0,1382	0,2048	0,2637	0,3087	0,3364	0,3456	0,3125
3	0,0011	0,0081	0,0244	0,0512	0,0879	0,1323	0,1811	0,2304	0,3105
4	0,0000	0,0005	0,0022	0,0064	0,0146	0,0283	0,0488	0,0768	0,1562
5	0,0000	0,0000	0,0001	0,0003	0,0010	0,0024	0,0053	0,0102	0,0312

Pourn= 10

$k/p$	0,05	0,10	0,15	0,20	0,25	0,30	0,35	0,40	0,50
0	0,5987	0,3487	0,1969	0,1074	0,0563	0,0282	0,0135	0,0060	0,0010
1	0,3151	0,3874	0,3474	0,2684	0,1877	0,1211	0,0725	0,0403	0,0098
2	0,0746	0,1937	0,2759	0,3020	0,2816	0,2335	0,1757	0,1209	0,0439
3	0,0105	0,0574	0,1298	0,2013	0,2503	0,2668	0,2522	0,2150	0,1172
4	0,0010	0,0112	0,0401	0,0881	0,1460	0,2001	0,2377	0,2508	0,2051
5	0,0001	0,0015	0,0085	0,0264	0,0584	0,1029	0,1536	0,2007	0,2461
6	0,0000	0,0001	0,0012	0,0055	0,0162	0,0368	0,0689	0,1115	0,2051
7	0,0000	0,0000	0,0001	0,0008	0,0031	0,0090	0,0212	0,0425	0,1172
8	0,0000	0,0000	0,0000	0,0001	0,0004	0,0014	0,0043	0,0106	0,0439
9	0,0000	0,0000	0,0000	0,0000	0,0000	0,0001	0,0005	0,0016	0,0098
10	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0001	0,0010

Pourn= 20

$k/p$	0,05	0,10	0,15	0,20	0,25	0,30	0,35	0,40	0,50
0	0,3585	0,1216	0,0388	0,0115	0,0032	0,0008	0,0002	0,0000	0,0000
1	0,3774	0,2702	0,1368	0,0576	0,0211	0,0068	0,0020	0,0005	0,0000
2	0,1887	0,2852	0,2293	0,1369	0,0669	0,0278	0,0100	0,0031	0,0002
3	0,0596	0,1901	0,2428	0,2054	0,1339	0,0716	0,0323	0,0123	0,0011
4	0,0133	0,0898	0,1821	0,2182	0,1897	0,1304	0,0738	0,0350	0,0046
5	0,0022	0,0319	0,1028	0,1746	0,2023	0,1789	0,1272	0,0746	0,0148
6	0,0003	0,0089	0,0454	0,1091	0,1686	0,1916	0,1712	0,1244	0,0370
7	0,0000	0,0020	0,0160	0,0545	0,1124	0,1643	0,1844	0,1659	0,0739
8	0,0000	0,0004	0,0046	0,0222	0,0609	0,1144	0,1614	0,1797	0,1201
9	0,0000	0,0001	0,0011	0,0074	0,0271	0,0654	0,1158	0,1597	0,1602
10	0,0000	0,0000	0,0002	0,0020	0,0099	0,0308	0,0686	0,1171	0,1762
11	0,0000	0,0000	0,0000	0,0005	0,0030	0,0120	0,0336	0,0710	0,1602
12	0,0000	0,0000	0,0000	0,0001	0,0008	0,0039	0,0136	0,0355	0,1201
13	0,0000	0,0000	0,0000	0,0000	0,0002	0,0010	0,0045	0,0146	0,0739
14	0,0000	0,0000	0,0000	0,0000	0,0000	0,0002	0,0012	0,0049	0,0370
15	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0003	0,0013	0,0148
16	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0003	0,0046
17	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0011
18	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0002

Valeurs de la fonction de répartition

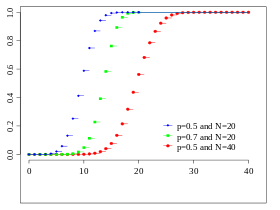
Les tables de valeurs suivantesdonnent les valeurs de la fonction de répartition de la loi binomialeb(n,p)pour différentes valeurs den.

Exemples: SiXsuit une loi$b(10\,;\,0,15)$,alors$\mathbb {P} (X\leq 4)\simeq 0,9901$.SiYsuit une loi$b(10\,;\,0,85)$,alors$\mathbb {P} (Y\leq 4)=\mathbb {P} (X\geq 6)=1-\mathbb {P} (X\leq 5)\simeq 1-0,9986=0,0014$.

Pourn= 5

$k/p$	0,05	0,10	0,15	0,20	0,25	0,30	0,35	0,40	0,50
0	0,7738	0,5905	0,4437	0,3277	0,2373	0,1681	0,1160	0,0778	0,0312
1	0,9774	0,9185	0,8352	0,7373	0,6328	0,5282	0,4284	0,3370	0,1875
2	0,9988	0,9914	0,9734	0,9421	0,8965	0,8369	0,7648	0,6826	0,5000
3	1,0000	0,9995	0,9978	0,9933	0,9844	0,9692	0,9460	0,9130	0,8125
4	1,0000	1,0000	0,9999	0,9997	0,9990	0,9976	0,9947	0,9898	0,9688
5	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000

Pourn= 10

$k/p$	0,05	0,10	0,15	0,20	0,25	0,30	0,35	0,40	0,50
0	0,5987	0,3487	0,1969	0,1074	0,0563	0,0282	0,0135	0,0060	0,0010
1	0,9139	0,7361	0,5443	0,3758	0,2440	0,1493	0,0860	0,0464	0,0107
2	0,9885	0,9298	0,8202	0,6778	0,5256	0,3828	0,2616	0,1673	0,0547
3	0,9990	0,9872	0,9500	0,8791	0,7759	0,6496	0,5138	0,3823	0,1719
4	0,9999	0,9984	0,9901	0,9672	0,9219	0,8497	0,7515	0,6331	0,3770
5	1,0000	0,9999	0,9986	0,9936	0,9803	0,9527	0,9051	0,8338	0,6230
6	1,0000	1,0000	0,9999	0,9991	0,9965	0,9894	0,9740	0,9452	0,8281
7	1,0000	1,0000	1,0000	0,9999	0,9996	0,9984	0,9952	0,9877	0,9453
8	1,0000	1,0000	1,0000	1,0000	1,0000	0,9999	0,9995	0,9983	0,9893
9	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	0,9999	0,9990
10	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000

Pourn= 20

$k/p$	0,05	0,10	0,15	0,20	0,25	0,30	0,35	0,40	0,50
0	0,3585	0,1216	0,0388	0,0115	0,0032	0,0008	0,0002	0,0000	0,0000
1	0,7358	0,3817	0,1756	0,0692	0,0243	0,0076	0,0021	0,0005	0,0000
2	0,9245	0,6769	0,4049	0,2061	0,0913	0,0355	0,0121	0,0036	0,0002
3	0,9841	0,8670	0,6477	0,4114	0,2252	0,1071	0,0444	0,0160	0,0013
4	0,9974	0,9568	0,8298	0,6296	0,4148	0,2375	0,1182	0,0510	0,0059
5	0,9997	0,9887	0,9327	0,8042	0,6172	0,4164	0,2454	0,1256	0,0207
6	1,0000	0,9976	0,9781	0,9133	0,7858	0,6080	0,4166	0,2500	0,0577
7	1,0000	0,9996	0,9941	0,9679	0,8982	0,7723	0,6010	0,4159	0,1316
8	1,0000	0,9999	0,9987	0,9900	0,9591	0,8867	0,7624	0,5956	0,2517
9	1,0000	1,0000	0,9998	0,9974	0,9861	0,9520	0,8782	0,7553	0,4119
10	1,0000	1,0000	1,0000	0,9994	0,9961	0,9829	0,9468	0,8725	0,5881
11	1,0000	1,0000	1,0000	0,9999	0,9991	0,9949	0,9804	0,9435	0,7483
12	1,0000	1,0000	1,0000	1,0000	0,998	0,9987	0,9940	0,9790	0,8684
13	1,0000	1,0000	1,0000	1,0000	1,0000	0,9997	0,9985	0,9935	0,9423
14	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	0,9997	0,9984	0,9793
15	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	0,9997	0,9941
16	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	0,9987
17	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	0,9998
18	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000

Tests et applications

Tests

D'une manière générale, untest statistiquepermet de rejeter, ou non, une hypothèse ditehypothèse nulle.L'idée principale est de prendre unéchantillonet de vérifier si l'hypothèse est vraie pour chaque élément de l'échantillon. Si on considère que les éléments sont indépendants, on compte donc le nombre d'éléments vérifiant une propriété, il y a donc présence de la loi binomiale. On compare si la proportion observée est significativement éloignée de la probabilité théorique de la loi binomiale.Ce test est appelé untest binomial.On peut utiliser aussi la loi normale lorsque la taille de l'échantillon est grand.

Il est possible d'effectuer un test statistique sur la conformité des valeurs des paramètres d'une loi de probabilité, notamment d'une loi binomiale, par rapport aux paramètres théoriques attendus pour la population étudiée.Le test de conformité de l'indice de dispersion s'applique dans ce cas.Cet indice de dispersion est le quotient de la somme des carrés des écarts et de la moyenne. Si$x_{k},\,k=1\dots n$sont les valeurs étudiées de moyenne notée${\bar {x}}$alors l'indice est:${\frac {1}{\bar {x}}}\sum _{k=1}^{n}(x_{k}-{\bar {x}})^{2}$.Grâce à uneLoi du χ²ou uneloi normale,le test rejette l'hypothèse de la valeur que prend le paramètrepde la loi binomiale.

Il est également possible de tester l'égalité de deux variables aléatoires de lois binomiales. Soient$X_{1}$et$X_{2}$deuxvariables aléatoiresde lois respectives$b(n_{1},p_{1})$et$b(n_{2},p_{2})$.On souhaite tester si$p_{1}=p_{2}=p$,c'est l'hypothèse$H_{0}$du test. Par lethéorème central limite,l'estimateur${\hat {p}}_{1}=X_{1}/n_{1}$suit uneloi normale${\mathcal {N}}(p_{1},p_{1}(1-p_{1})/n_{1})$lorsque$n_{1}$est grand. Il en est de même avec${\hat {p}}_{2}$.En considérant l'hypothèse$H_{0}$vraie, on peut montrer que$Z={\frac {{\hat {p}}_{1}-{\hat {p}}_{2}}{\sqrt {p(1-p)(1/n_{1}+1/n_{2})}}}$suit une loi normale centrée réduite.On rejette alors l'hypothèse$H_{0}$au niveau de confiance 0,95 si$|Z|>1,96$.

Autres applications

Par définition la somme de variables aléatoires indépendantes deloi de Bernoullisuit une loi binomiale. Un exemple typique de phénomène suivant une loi de Bernoulli est le lancer d'une pièce pour unpile ou face.Le nombre de succès, par exemple le nombre de fois où l'on obtient pile, suit donc une loi binomiale. De nombreuses situations peuvent être modélisées par cet exemple ce qui donne son importance à la loi.

Engénétique,lors de la reproduction, chaquegèneest composée de deuxallèlesqui sont issus des deux parents. Soit les deux allèles proviennent du même parent, soit chaque parent transmet un allèle. Il est alors possible de faire une liste de différents allèles et de noter ces deux cas. Le nombre d'allèles issus du même parent peut être modélisé par une variable aléatoire de loi binomiale.Pour savoir s'il y a égale probabilité d'allèle de même provenance ou de provenance différente, on peut étudier un test statistique.Inversement, pour simuler les allèles d'un individu, il est possible de simuler les fréquences des allèles par des variables aléatoires binomiales.

Exemple de marche aléatoire (renormalisée). La position de la marche suit une loi binomiale.

Enlinguistique,la loi binomiale est utilisée pour étudier la richesse du vocabulaire d'un texte.C'est un outil quantitatif qui permet de mesurer la fréquence d'un mot dans un texte indépendamment de la longueur du texte. Plus précisément la méthode de Müller permet d'évaluer la richesse théorique du vocabulaire d'un texte grâce au vocabulaire d'un texte plus long, et ainsi comparer avec la richesse du vocabulaire du texte court en question. Techniquement, si$N_{a}$est le nombre de mots d'un texte et$N_{b}$celui d'un autre texte. Alors$p={\frac {N_{a}}{N_{a}+N_{b}}}$est la probabilité d'apparition d'un mot tiré au hasard dans le premier texte; de même pour$q={\frac {N_{b}}{N_{a}+N_{b}}}$dans le deuxième texte.Le nombre de mots ayant la même fréquence d'apparition dans le premier texte suit alors une loi binomiale de paramètres$n=N_{a}+N_{b}$etp.Il est possible d'effectuer des tests statistiques pour conclure si la richesse du vocabulaire est grande ou non.

En 1908,Émile Borelétudie la fréquence des différents chiffres dans ledéveloppement décimald'unnombre réel.Il considère les2npremières valeurs de la décomposition décimale et estime la probabilité d'obtention du nombre de fois où apparaît chaque entier dans cette décomposition grâce à l'approximation par la loi normale. Il démontre ainsi le théorème desnombres normaux.

Unemarche aléatoiresur$\mathbb {Z}$est unprocessus stochastique$(S_{n},n\in \mathbb {N} ^{*})$à temps entier.C'est-à-dire que la marche part d'une valeur initialeS₀= 0par exemple et à chaque unité de temps, le marcheur se déplace (indépendamment du chemin parcouru avant) d'un pas vers le haut avec une probabilitépou d'un pas vers le bas avec une probabilité1 –p,ainsiS₁= –1ou1.S_ndonne la position du marcheur au bout d'un tempsn.Sip= 1 –p= 0,5,la marche est dite symétrique et le marcheur a autant de chance d'aller vers le haut que vers le bas. Dans ce cas, au bout du tempsn,la variable aléatoire${\frac {1}{2}}(S_{n}+n)$peut prendre comme valeurs$0,1\dots n$et elle est de loi binomialeb(n,0,5).Cette considération ainsi que la convergence vers la loi normale (voirci-dessus) permet de démontrer qu'une marche aléatoire renormalisée converge vers lemouvement brownien(voirThéorème de Donsker).

Notes et références

Articles et autres sources

Voir aussi

Bibliographie

:document utilisé comme source pour la rédaction de cet article.

• Patrick Bogaert,Probabilités pour scientifiques et ingénieurs: Introduction au calcul des probabilités,De Boeck Supérieur,2005,402p.(ISBN2-8041-4794-0,lire en ligne)
• Jean-Pierre Courtin,L'Homme et les lois de la nature,vol.1,Lulu.com,2012(ISBN978-1-4710-3427-5,lire en ligne)
• Pierre Dagnelie,Statistique théorique et appliquée,vol.2, Paris/Bruxelles, De Boeck Supérieur,1998,659p.(ISBN2-8041-2802-4)
• (en)Holger Dette et William J. Studden,The Theory of Canonical Moments with Applications in Statistics, Probability, and Analysis,John Wiley & Sons,1997(lire en ligne)
• Yadolah Dodge,Statistique: Dictionnaire encyclopédique,Springer Science+Business Media,2007,662p.(ISBN978-2-10-058102-3,lire en ligne)
• Dominique Foata, Aimé Fuchs et Jacques Ranchi,Calcul des probabilités: Cours, exercices et problèmes corrigés,Paris/Berlin/Heidelberg etc.,Dunod,2012,3^eéd.,368p.(ISBN978-2-287-72093-2,lire en ligne)
• (en)Eric Gossett,Discrete Mathematics with Proof,Hoboken (N.J.),John Wiley & Sons,2009,904p.(ISBN978-0-470-45793-1,lire en ligne)
• (en)Anders Hald,A History of Probability and Statistics and Their Applications before 1750,John Wiley & Sons,2005,608p.(ISBN0-471-47129-1,lire en ligne)
• (en)Michiel Hazewinkel,Encyclopaedia of Mathematics (set),vol.2, Dordrecht/Boston/London,Springer Science+Business Media,1994,963p.(ISBN1-55608-010-7,lire en ligne)
• (en)Hans-Joachim Mittag et Horst Rinne,Statistical Methods of Quality Assurance,CRC Press,1993,664p.(ISBN0-412-55980-3,lire en ligne)
• (en)Norman Johnson, Adrienne Kemp et Samuel Kotz,Univariate Discrete Distributions,John Wiley & Sons,2005,646p.(ISBN0-471-27246-9,lire en ligne)
• (en)Emmanuel Lesigne,Heads or tails: an introduction to limit theorems in probability,Providence (R.I.),AMS,2005,150p.(ISBN0-8218-3714-1,lire en ligne)
• Charles-Edouard Pfister,Théorie des probabilités: cours d'introduction avec application à la statistique mathématique,Lausanne,PPUR,2012,229p.(ISBN978-2-88074-981-1,lire en ligne)
• Alan Ruegg,Probabilités et statistique,vol.3, PPUR,1994,153p.(ISBN2-88074-286-2,lire en ligne)
• (en)David Siegmund et Benjamin Yakir,The Statistics of Gene Mapping,Springer Science+Business Media,2007,354p.(lire en ligne)

Articles connexes

• Arbre de probabilité
• Loi de Bernoulli
• Loi de Poisson
• Loi de probabilité
• Loi multinomiale
• Loi normale
• Théorème de Moivre-Laplace
• Loi binomiale négative

Liens externes

• Ressource relative à la santé:
  • Medical Subject Headings
• Notices dans des dictionnaires ou encyclopédies généralistes:

  • Britannica
  • Den Store Danske Encyklopædi
  • Store norske leksikon
• Notices d'autorité:

  • LCCN
  • GND
  • Israël
  • Tchéquie
  • Lettonie
• (en)Eric W. Weisstein,«Binomial Distribution», surMathWorld