Loi de Rice

Rice
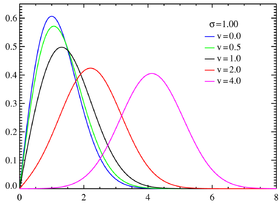Densité de probabilité pour différentes valeurs deνavec σ = 1. pour différentes valeurs deνavec σ = 0,25.
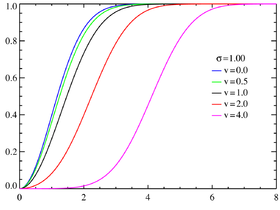Fonction de répartition avec σ = 1,0 pour différentes valeurs deν. avec σ = 0,25 pour différentes valeurs deν.
Paramètres	$\nu \geq 0\,$ $\sigma \geq 0\,$
Support	$x\in [0;\infty )$
Densité de probabilité	${\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}}\right)$
Fonction de répartition	$1-Q_{1}\left({\frac {\nu }{\sigma }},{\frac {x}{\sigma }}\right)$ où$Q_{1}$est lafonction Q de Marcum
Espérance	$\sigma {\sqrt {\pi /2}}\,\,L_{1/2}(-\nu ^{2}/2\sigma ^{2})$
Variance	$2\sigma ^{2}+\nu ^{2}-{\frac {\pi \sigma ^{2}}{2}}L_{1/2}^{2}\left({\frac {-\nu ^{2}}{2\sigma ^{2}}}\right)$
Asymétrie	(compliqué)
Kurtosis normalisé	(compliqué)

Enstatistiquesetthéorie des probabilités,laloi de Rice,nommée d'aprèsStephen O. Rice(en)(1907–1986),est uneloi de probabilitéà densité(c'est-à-dire continue).

C'est une généralisation de laloi de Rayleighutilisée pour décrire le comportement d'un signal radio qui se propage selon plusieurs chemins (multipath) avant d'être reçu par une antenne.

Caractérisation

Soient deuxvariables de Gausscentrées, indépendantes, de même varianceσ².Si on considère qu'elles représentent les deux coordonnées d'un point d'un plan, la distance de ce point à l'origine suit uneloi de Rayleigh:

$f(x,\sigma )={\frac {x}{\sigma ^{2}}}\exp \left({\frac {-x^{2}}{2\sigma ^{2}}}\right)$.

En supposant que la distribution est centrée sur un point de coordonnées(ν cos θ, ν sin θ)(coordonnées polaires(ν, θ)), la densité de probabilité devient:

$f(x|\nu,\sigma )={\frac {x}{\sigma ^{2}}}\exp \left({\frac {-(x^{2}+\nu ^{2})}{2\sigma ^{2}}}\right)I_{0}\left({\frac {x\nu }{\sigma ^{2}}}\right)$

oùI₀(z)est lafonction de Besselmodifiée de première espèce et d'ordre 0.

Propriétés

Moments

Les premiersmoments (non centrés)sont:

$\mu _{1}=\sigma {\sqrt {\pi /2}}\,\,L_{1/2}(-\nu ^{2}/2\sigma ^{2})$

$\mu _{2}=2\sigma ^{2}+\nu ^{2}\,$

$\mu _{3}=3\sigma ^{3}{\sqrt {\pi /2}}\,\,L_{3/2}(-\nu ^{2}/2\sigma ^{2})$

$\mu _{4}=8\sigma ^{4}+8\sigma ^{2}\nu ^{2}+\nu ^{4}\,$

$\mu _{5}=15\sigma ^{5}{\sqrt {\pi /2}}\,\,L_{5/2}(-\nu ^{2}/2\sigma ^{2})$

$\mu _{6}=48\sigma ^{6}+72\sigma ^{4}\nu ^{2}+18\sigma ^{2}\nu ^{4}+\nu ^{6}\,$

$L_{\nu }(x)=L_{\nu }^{0}(x)=M(-\nu,1,x)=\,_{1}F_{1}(-\nu;1;x)$

où,L_ν(x)représente unpolynôme de LaguerreetMdésigne lafonction hypergéométrique confluente.

Pour le casν= 1/2:

$L_{1/2}(x)=\,_{1}F_{1}\left(-{\frac {1}{2}};1;x\right)$

$=\mathrm {e} ^{x/2}\left[\left(1-x\right)I_{0}\left({\frac {-x}{2}}\right)-xI_{1}\left({\frac {-x}{2}}\right)\right].$

Généralement les moments sont donnés par

$\mu _{k}=s^{k}2^{k/2}\,\Gamma (1\!+\!k/2)\,L_{k/2}(-\nu ^{2}/2\sigma ^{2}),\,$

oùs= σ^1/2.

Lorsquekest pair, les moments deviennent des polynômes enσetν.

Distributions liées

• La variable$r={\sqrt {x^{2}+y^{2}}}$suit une loi de Rice$R\sim \mathrm {Rice} \left(\sigma,\nu \right)$à condition que$X\sim {\mathcal {N}}\left(\nu \cos \theta,\sigma ^{2}\right)$et$Y\sim {\mathcal {N}}\left(\nu \sin \theta,\sigma ^{2}\right)$soient deux variablesgaussiennesindépendantes.
• Pour obtenir une variable$R\sim \mathrm {Rice} \left(\nu,\sigma \right)$,on peut considérer une autre procédure:

1. TirerPselon uneloi de Poisson,de paramètre$\lambda ={\frac {\nu ^{2}}{2\sigma ^{2}}}.$
2. TirerXselon uneloi duχ²avec2P+ 2degrés de liberté.
3. PoserR=σ√X.

• Si$R\sim \mathrm {Rice} \left(1,\nu \right)$alorsR²suit une loi duχ²non centrée, à 2 degrés de liberté et un paramètre de non-centralitéν².

Cas limites

Pour de grandes valeurs de l'argument, le polynôme de Laguerre devient:

$L_{\nu }(x)\ {\underset {x\rightarrow -\infty }{\sim }}\ {\frac {|x|^{\nu }}{\Gamma (1+\nu )}}.$

On peut constater que lorsqueνdevient grand ou queσdevient petit, alors la moyenne devientνet la varianceσ².

Notes et références

• (en)Stephen O. Rice, « Mathematical Analysis of Random Noise », dansBell System Technical Journal,vol. 24, 1945,p.46–156
• (en)I. Soltani Bozchalooi et Ming Liang, « A smoothness index-guided approach to wavelet parameter selection in signal de-noising and fault detection », dansJournal of Sound and Vibration,vol. 308,n^o1-2, 2007,p.246–267DOI10.1016/j.jsv.2007.07.038
• (en)John G. Proakis,Digital Communications,McGraw-Hill, 2000

• (en)Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé«Rice distribution»(voir la liste des auteurs).

Liens externes

• (en)Le siteSOCRfournit les ressources suivantes:interactive Rice distribution,Rice simulation, model-fitting and parameter estimation.
• (en)Multipath Receptionpour la signification
• (en)Complex Gaussian distributionpour l'aspect mathématique
• (en)MATLAB code for Rice distribution(densité de probabilité, moyenne,varianceet génération de nombres aléatoires)