Nombre complexe

Enmathématiques,l'ensemble desnombres complexesest actuellement défini comme uneextensionde l'ensemble desnombres réels,contenant en particulier unnombre imaginairenotéi[a],[b]tel quei2= −1.Le carré de(−i)est aussi égal à −1:(−i)2= −1.Tout nombre complexe peut s'écrire sous la formex+ iyoùxetysont desnombres réels.
Les nombres complexes ont été progressivement introduits auXVIesièclepar l’école mathématique italienne (Jérôme Cardan,Raphaël Bombelli,Tartaglia) afin d'exprimer les solutions deséquations du troisième degréen toute généralité par lesformules de Cardan,en utilisant notamment des « nombres » decarrénégatif.
On peut munir l'ensemble des nombres complexes d'une addition et d'une multiplication qui en font uncorps commutatifcontenant le corps des nombres réels. Il est appelécorps des nombres complexeset se noteℂ.La notion devaleur absoluedéfinie sur l'ensemble des nombres réels peut être étendue à l'ensemble des nombres complexes et prend alors le nom demodule.Mais on ne peut pas munir l'ensemble des nombres complexes d'unerelation d'ordrequi en ferait uncorps totalement ordonné,c'est-à-dire qu'il n'est pas possible de comparer deux complexes en respectant les règles opératoires valables pour les nombres réels.
Ce n'est qu'à partir duXIXesiècle,sous l'impulsion de l'abbé Buéeet deJean-Robert Argand(plan d'Argand), puis avec les travaux deGausset deCauchy,que se développe l'aspect géométrique des nombres complexes. On les associe à desvecteursou despointsdu plan. Lestransformationsduplans'expriment alors sous forme de transformations complexes.
En algèbre, lethéorème de d'Alembert-Gaussénonce qu'unpolynômecomplexe non constant possède toujours au moins uneracinecomplexe. Le corps des nombres complexes est ditalgébriquement clos.On peut ainsi identifier ledegréd'un polynôme complexe non nul au nombre de sesracinescomptées avec leurordre de multiplicité.
En analyse, l'exponentielle complexepermet de simplifier l'étude desséries de Fourier,puis de définir latransformée de Fourier.La branche de l'analyse complexeconcerne l'étude des fonctionsdérivablesau sens complexe, appelées fonctionsholomorphes.
Enphysique,les nombres complexes sont utilisés pour décrire le comportement d'oscillateurs électriquesou les phénomènesondulatoiresenélectromagnétisme(Re(eiωt)représentant une sinusoïde). Dans le domaine de l'électricitéet notamment de l'électrocinétique,on note souventjl'unité imaginaire,la notation usuelle pouvant prêter à confusion avec le symbole d'uneintensité électrique.Ils sont aussi essentiels dans la formulation mathématique de lamécanique quantique.
Présentation informelle[modifier|modifier le code]
En guise de présentation informelle, on s'appuie sur la représentation géométrique des nombres complexes, comme expliquée dans le chapitre 5 deÀ la découverte des lois de l'univers: La prodigieuse histoire des mathématiques et de la physiquedeRoger Penrose.
Passage d'une dimension à deux dimensions[modifier|modifier le code]
Un nombre réel est un nombre que l'on peut représenter comme un point sur un axe à une dimension. On trouve le zéro, les nombresentiers naturelscomme le zéro, 1, 2, 3..., les nombres relatifs négatifs comme -1, -2, -3,..., lesnombres rationnelscomme 2/3, 4/9, -8/11, etc., et d'autres nombres réels comme(racine de 2). Vu que l'espace est en une dimension (c'est une ligne), un tel nombre réel se représente par une seule coordonnée: le nombre lui-même.

La notion de nombre complexe étend la notion de nombre pour représenter un point dans le plan. Un tel point se représente par deux coordonnées: une abscissexet une ordonnéey.Les nombresxetysont des nombres réels. Ce point dans le plan représente alors unnombre complexe.Un nombre réelxest représenté par un point d'abscissexet d'ordonnée nulle. Bref, l'axe à une dimension des nombres réels est l'axe des abscisses dans le plan.

Le nombre i[modifier|modifier le code]
Additionner 1 et 2 donne 3. En additionnant deux nombres réels on obtient toujours un nombre réel. On reste sur l'axe des abscisses. Afin de sortir de cet axe, on a besoin d'au moins d'un nombre qui sort de cet axe: par exemple, le nombre qui correspond au point d'abscisse 0 et d'ordonnée 1. On note ce nombrei.
Notation x + yi[modifier|modifier le code]
Le nombre réel 2 peut s'écrire 2×1. C'est-à-dire que l'on vient doubler la longueur du vecteur correspondant à la flèche partant de l'origine finissant au point correspondant à 1. On obtient un point qui est sur l'axe des abscisses. De la même façon, on peut allonger/rétrécir le vecteur correspondant à i. Par exemple 3×i est le point d’abscisse nulle et d'ordonnée 3. On obtient un point qui est sur l'axe des ordonnées. En faisant une addition, on peut obtenir n'importe quel point du plan. Par exemple, 2,5+3i est le point d’abscisse 2,5 et d'ordonnée 3; -3-4i est le point d'abscisse -3 et d'ordonnée -4.

Addition[modifier|modifier le code]
L'addition d'un nombre complexezet d'un autre nombre complexews'obtient, en prenant le point pourz,et en letranslatantpar le vecteur correspondant à la flèche partant de l'origine et finissant au pointw.
Multiplication[modifier|modifier le code]
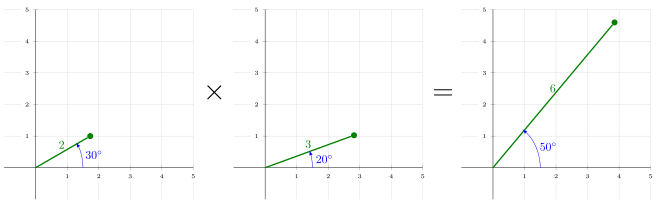
Considérons 2+3i. Multiplier par 2 ce nombre consiste à doubler le vecteur partant de l'origine finissant au point d’abscisse 2 et d'ordonnée 3. On obtient le nombre complexe 4+6i. Bref, multiplier par un nombre réel revient à allonger/rétrécir/changer de sens le vecteur associé au point. Multiplier par un nombre complexe est plus subtil. Cela revient non seulement à allonger/rétrécir le vecteur mais aussi à le pivoter,en additionnant les angles[pas clair].Plus précisément, pour chaque nombre complexe (i.e. un point du plan), on considère l'angle entre l'axe des abscisses et le vecteur correspondant à la flèche partant de l'origine finissant en ce point. L'exemple ci-dessous considère deux nombres complexes. L'un est obtenu en avançant d'une distance de 2 avec un angle de 30°, et l'autre en avançant de 3 avec un angle de 20°. Le produit de ces deux nombres est le point obtenu en avançant de 6 (2 fois 3) avec un angle de 50° (20° + 30°).
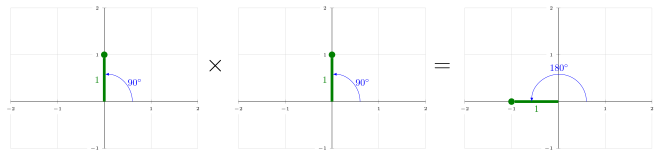
Pourquoii2= −1?[modifier|modifier le code]
Le nombrei2vauti×i:on multiplieipari.Le nombreicorrespond au point d’abscisse nulle et d'ordonnée 1. On remarque un angle de 90° entre l'axe des abscisses et le vecteur correspondant au nombrei(c'est l'angle entre l'axe des abscisses et des ordonnées). Faire la multiplication deiparirevient à additionner les angles:90° + 90° = 180°.On se trouve donc dans l'autre sens sur l'axe des abscisses et on obtient le point d’abscisse −1 et d'ordonnée 0, qui n'est autre que la représentation du nombre −1.

Motivation[modifier|modifier le code]
Laméthode de Cardanfournit une solution deséquations du troisième degré,à condition de pouvoir résoudre une équation auxiliaire du second degré. Or cela est impossible lorsque sondiscriminantest négatif, alors qu’on sait que l’équation initiale admet des solutions. Cardan lui-même s’est enhardi à introduire dans ce cas des nombres « imaginaires » de carré négatif, constatant qu’alors sa méthode fonctionnait et produisait bien les solutions de l’équation initiale. Il est clair que si l’on admet l’existence deitel quei2= –1, on doit aussi introduire tous les « nombres » de la formea+bi(oùaetbsont des nombres ordinaires). Il aura fallu deux siècles pour que les mathématiciens se convainquent que ces nombres « absurdes », loin d’amener à des résultats contradictoires, étaient au contraire d’une grande utilité dans de nombreux domaines fort éloignés des questions algébriques qui leur avaient donné naissance.
Présentation[modifier|modifier le code]
Les nombres complexes, notés habituellementz,peuvent être présentés sous plusieurs formes, algébriques, polaires, ou géométriques.
Forme algébrique[modifier|modifier le code]
Un nombre complexezse présente en général sous forme algébrique comme une sommea+ ib,oùaetbsont desnombres réelsquelconques et oùi(l’unité imaginaire) est un nombre particulier tel quei2= –1. Le réelaest appelépartie réelledezet se noteRe(z)ouℜ(z),le réelbest sapartie imaginaireet se noteIm(z)ouℑ(z).Deux nombres complexes sont égaux si et seulement s'ils ont la même partie réelle et la même partie imaginaire.
Un nombre complexezest ditimaginaire puroutotalement imaginairesi sa partie réelle est nulle, dans ce cas il s'écrit sous la formez=ib.Un nombre complexe dont la partie imaginaire est nulle est dit réel. Le nombre réel 0 est le seul qui soit à la fois réel et imaginaire pur. Bien sûr la plupart des nombres complexes ne sont ni réels ni imaginaires purs. Dans les textes anciens, de tels nombres, avant de s'appeler « complexes », s'appelaient « imaginaires », ce qui explique l'habitude persistante d'appeler « imaginaires purs » ceux ne comportant pas de partie réelle.
Forme polaire[modifier|modifier le code]
Pour tout couple de réels(a,b)différent du couple (0,0), il existe un réel positifret une famille d'anglesθdéterminés à un multiple de 2π près tels quea=rcos(θ)etb=rsin(θ).Tout nombre complexe non nul peut donc s'écrire sous uneforme trigonométrique:z = r(cos(θ) + i sin(θ))avecr> 0.
Le réel positifrest appelé lemoduledu complexezet est noté |z|.
Le réelθest appelé unargumentdu complexezet est notéarg(z).
On écrit parfois ce même complexe sous les formes suivantes:
- z=reiθ,forme exponentielleutilisant laformule d'Euler
- z= (r,θ) =r∠θ,forme polaire
- z=r(cosθ+ i sinθ) = r cis(θ)(ce qui définit lanotation cis[1])
Le module du complexezest laracine carréede la somme des carrés des parties réelles et imaginaires:
Pour calculer un argument θ à partir de la forme algébriquea+ ib,on peut utiliser les fonctionsarccos,arcsinouarctan:
Par exemple, les réels strictement positifs ont un argument multiple de2π,les réels strictement négatifs ont pour argument un multiple impair deπ.
Les imaginaires purs non nuls ont un argument congru àπ/2ou –π/2modulo2π,selon le signe de leur partie imaginaire.
Forme géométrique[modifier|modifier le code]

Dans unplan complexemuni d'unrepèreorthonormé,l'imaged'un nombre complexez = a+ ibest le pointMde coordonnées (a,b), sonimage vectorielleest le vecteur.Le nombrezest appeléaffixe[2],[3]du pointMou du vecteur(dans ce contexte, affixe est féminin: une affixe).
Le module |z| est alors lalongueurdu segment [OM]: c'est la distance de l'origineOdu repère au pointM.
Sizest différent de 0, son image est distincte de l'origineOdu repère. On appelle argument dezn'importe quelle mesureθen radians de l'angle,bien définie à un multiple de2πprès.
Puisque tous les plans complexes sontcanoniquementisomorphes,on parle du plan complexe sans préciser davantage.
Une extension de cette représentation graphique des nombres complexes est lacoloration de régions[4].Celle-ci permet la représentation dans le plan complexe d'unefonction complexef(z). La valeur d'une telle fonction étant elle-même un nombre complexe, nécessiterait une représentation à 4 dimensions. La coloration de régions utilise des moyensinfographiquespour associer l'argument à lacouleuret le module à laluminosité.
Opérations et relations[modifier|modifier le code]
Addition[modifier|modifier le code]
Forme algébrique[modifier|modifier le code]
Dans l'ensemble des nombres complexes, on définit une addition de la manière suivante: Cette opération estassociative,commutative,possède unélément neutre(le complexe nul) et tout complexe possède un opposé:opp(a+ ib) = –a+i (–b) L'ensemble des nombres complexes muni de l'addition forme donc ungroupe commutatif.
Interprétation géométrique[modifier|modifier le code]
SiMetM' sont les points d'affixeszetz', l'imageM "de la sommez+z'est définie par la relation Pour tout complexez0,la transformation qui, au pointMd'affixez,associe le pointM'd'affixez'=z+z0est une translation de vecteurud'affixez0.
Multiplication[modifier|modifier le code]
Forme algébrique[modifier|modifier le code]
Dans l'ensemble des nombres complexes, on définit une multiplication de la manière suivante: Cette opération est associative, commutative,distributivepour l'addition et possède un élément neutre 1. Puisquer× i = i ×r,un complexe est noté indifféremmenta+ iboua + bi
Ces propriétés permettent d'obtenir l'égalité suivante: Puisque la sommea2+b2de deux carrés de nombres réels est un nombre réel strictement positif (sauf sia = b =0), il existe un inverse à tout nombre complexe non nul avec l'égalité:
L'ensemble des nombres complexes munis de l'addition et de la multiplication est donc uncorps commutatif.De plus, l'ensemble des nombres complexes muni de l'addition et de la multiplication par un réel est unespace vectorielsur ℝ dedimension2
Forme polaire[modifier|modifier le code]
Cette écriture est adaptée au calcul du produit de deux nombres complexes du fait desformules d'addition:
Ces identités, appliquées à la forme trigonométrique des nombres complexes, permettent d'énoncer les règles suivantes:
- le produit de deux nombres complexes non nuls a pour module le produit des modules et pour argument la somme des arguments;
- le quotient de deux nombres complexes non nuls a pour module le quotient des modules et pour argument la différence des arguments.
La forme exponentielle met en évidence ces propriétés
La forme polaire est également bien adaptée pour calculer la puissance d'un nombre complexe par laformule de Moivre:
Interprétation géométrique[modifier|modifier le code]

SiMest le point d'affixezet siλest un réel, l'imageM' du produitλzest définie par la relation
L'action du nombre réelλpar multiplication scalaire s'interprète géométriquement comme unehomothétiede centreOet de rapportλsur le plan complexe.
SiMest le point d'affixezet siz0est un complexe de module 1 et d'argumentθ,l'imageM' du produitz0zest définie par les relations
- .
L'action d'un nombre complexe de module 1 par multiplication s'interprète géométriquement comme unerotationde centre l'origine et d'angle l'argument.
Par composition d'une homothétie et d'une rotation, l'action d'un nombre complexeznon nul par multiplication s'interprète géométriquement comme unesimilitude directede centre l'origine, de rapport |z| et d'anglearg(z).
L'image de l'inverse1/zdezest l'image deMpar l'inversionpar rapport au cercle unité, composée avec la symétrie par rapport à l'axe des abscisses.
Conjugaison[modifier|modifier le code]

Lecomplexe conjuguédu nombre complexez=a+ ibesta− ib.Il est notézouz*.Le conjugué d'un complexe a donc même partie réelle que le complexe de départ mais une partie imaginaire opposée. Le complexe conjugué d'un complexe non nul a même module que le complexe de départ mais un argument opposé.
Le conjugué d'une somme, d'une différence, d'un produit ou d'un quotient est respectivement la somme, la différence, le produit ou le quotient des conjugués. Le conjugué du conjugué d'un complexe est le complexe de départ. L'application de conjugaison est donc unautomorphismeinvolutif.
SiMest le point d'affixez,l'image du complexezest lesymétriquedeMpar rapport à l'axe des abscisses.
Partie réelle, partie imaginaire et module d'un complexe peuvent se définir à l'aide du complexe et de son conjugué:
Module[modifier|modifier le code]
Le module d'un nombre complexe s'interprète, dans le plan complexe comme la distance séparant l'image de ce complexe de l'origine du repère. SiMetM 'sont les points d'affixeszetz',|z' – z|est la distanceM'M.
Le seul nombre complexe de module nul est le réel nul. Puisque le module du produit ou du quotient de deux complexes non nuls est respectivement le produit ou le quotient de leurs modules, l'application
est unmorphisme de groupesmultiplicatifs.
L'interprétation du module comme unedistanceconduit à l'inégalité triangulairesuivante:L'application module est unevaleur absoluecar elle est strictement positive en dehors de 0,sous-additiveet multiplicative.
Relation d'ordre[modifier|modifier le code]
Dans uncorps totalement ordonné,tout carré est positif et l'opposé d'un nombre positif non nul est négatif. Ces deux propriétés sont en contradiction avec le fait que dans le corps des nombres complexes 1 et son opposé –1 sont tous deux des carrés (de 1 et de i) mais ne peuvent pas être tous deux positifs. Il n'est donc pas possible de munir le corps des complexes d'une relation d'ordre total compatible avec les deux opérations.
On peut cependant munir le corps des complexes d'un ordre partiel compatible avec la somme et le produit en posant:a+ ib<a'+ ib'si et seulement sia<a'etb=b'.On peut également munir l'ensemble des complexes, considéré comme un espace vectoriel sur ℝ, d'une relation d'ordre total,compatible avec l'addition, ainsi qu’avec la multiplication par des réels positifs, grâce à l'ordre lexicographique:a+ ib<a'+ ib'si et seulement sia<a'oua=a'etb<b'.
Racine[modifier|modifier le code]
La forme polaire d'un complexe permet de mettre en évidence le fait qu'un nombre complexe non nul possède exactementnracines nièmes, de même module égal àn√ret d'argumentθ+ 2kπn.
Pour tout entier natureln,l'ensemble des racines nièmes de l'unitéUnest ungroupemultiplicatifisomorpheaugroupe additif ℤ/nℤdes congruences modulon.
On peut démontrer que toutpolynômeà coefficients complexes possède au moins uneracinecomplexe. C'est lethéorème fondamental de l'algèbre.Cette propriété fait du corps des complexes uncorps algébriquement clos.Un polynôme à coefficients complexes est donc entièrement factorisable en produit de polynômes de degré 1 et possède donc un nombre de racines (comptées avec leurordre de multiplicité) égal audegré du polynôme.
Exponentiation et logarithme[modifier|modifier le code]
Laformule d'Eulercosθ+ i sinθ= eiθqui se démontre à l'aide de limite de suites, ou d'équation différentielle permet de justifier la notation exponentielle des nombres complexes.
Lafonction exponentiellese prolonge en une fonction de la variable complexe de la manière suivante:en conservant les propriétés algébriques de l'exponentielle. L'exponentielle complexe est un morphisme du groupe additif (ℂ,+) dans le groupe multiplicatif (ℂ*,×), ℂ* ensemble des nombres complexes non nuls.
Cependant lafonction logarithmene peut pas se prolonger en une fonction complexe en gardant ses propriétés. Dans l'histoire des nombres complexes,cette découverte a fait l'objet de nombreux échanges de lettres entre mathématiciens telsJean Bernoulli,Gottfried Wilhelm LeibnizetLeonhard Euler.On peut le définir de manièremultivaluéeen posantformule dans laquellearg(z)est défini à un multiple de 2πprès.
Structures[modifier|modifier le code]
L'ensemble des nombres complexes est donc uncorps commutatifalgébriquement closnontotalement ordonnable.
En fait, le corps des complexes est laclôture algébriquedu corps des réels, c'est-à-dire le plus petit corps qui contienne le corps des réels et qui soit algébriquement clos. Du point de vue de lathéorie de Galois,on peut considérer les automorphismes du corps des complexes: l'identité et la conjugaison sont ses seuls automorphismes continus (on peut remplacer l'hypothèse « continu » par, au choix, « mesurable » ou « tel que l'image de tout réel est un réel »). En supposant l'axiome du choix on peut construire des automorphismes « exotiques » de ce corps: voirAutomorphismes de corps non continus de ℂ.
C'est également unespace vectorielsur ℝ totalement ordonné par l'ordre lexicographique.
Construction[modifier|modifier le code]
Il existe plusieurs manières courantes de construire le corps des nombres complexes à partir de l'ensemble des nombres réels et de ses opérations arithmétiques élémentaires. Outre que les objets ainsi définis sont tousisomorphes,les constructions présentées ci-après mettent en lumière trois caractéristiques importantes:
- Le corps des réels est clairement identifié comme un sous-ensemble du corps des complexes et les opérations d'addition et de multiplication sont préservées dans la nouvelle structure. Le nombre réel 1 resteneutrepour la multiplication.
- Il existe un nombre complexeicanoniquementchoisi dont le carré vaut –1 (son opposé vérifie aussi cette propriété, et le choix fait dans chacune des constructions présentées est donc en fait arbitraire, mais cela n'a pas d'importance en pratique).
- Deux paramètres réels sont nécessaires et suffisants pour décrire tous les nombres complexes, ce qui souligne la structure d'espace vectoriel réel de dimension 2 avec unebase canonique.
Couples de réels[modifier|modifier le code]
On peut définir un nombre complexe comme un couple (a,b) de nombres réels. Sur l'ensemble ℝ2des couples de réels on définit une addition et une multiplication.
Cette construction est essentiellement la « théorie des couples algébriques » due au mathématicienWilliam Rowan Hamiltonqui l'ayant conçue vers 1826, l'expose devant l'Académie Royale d'Irlande en 1833, et la publie en 1835.Carl Friedrich Gaussarrive à des résultats voisins en 1831 qu'il publie en 1837. Hamilton se préoccupait de justifier l'« existence » des nombres complexes. Ce qui est présenté ci-dessous comme de simples définitions, justifiées implicitement par les règles de calcul sur les nombres complexes mais indépendantes d'une existence préalable de ceux-ci, est le fruit d'une longue analyse chez Hamilton[5].
L'addition est celle des composantes terme à terme:
- .
La multiplication est définie par:
- .
On vérifie alors que ℝ2muni de ces deux lois, avec (0, 0) comme neutre additif et (1, 0) comme neutre multiplicatif, est un corps; en particulier, l'inverse d'un élément (a,b) ≠ (0, 0) est(a/(a2+b2), –b/(a2+b2)),et (0, 1)×(0, 1) = (–1, 0).
L'ensemble des réels s'identifie alors à la droite ℝ×{0} et l'élémentiest le couple (0, 1).
L'ensemble ℝ2peut être muni de sa structure canonique deplanvectoriel euclidien. Un nombre complexe est alors un vecteur du plan ℝ2.La somme complexe est la somme vectorielle. La base canonique est constituée de deux vecteurs correspondant pour le premier (1, 0) au nombre complexe 1 et pour le second au nombre complexei.
On peut introduire enfin lemodule d'un nombre complexequi correspond à lanorme euclidiennedu vecteur associé et l'argumentqui est une mesure de l'angle formé par le vecteur associé avec le premiervecteur de base.
Cette définition présente l'avantage de la simplicité, puisqu'elle exige peu de prérequis mathématiques. Elle est en outre adaptée à lareprésentation géométriquedes nombres complexes.
Matrice de similitude[modifier|modifier le code]
Il est intéressant de définir un nombre complexe non nul comme unematricedesimilitude directeà coefficients réels, car lesopérations matriciellesinduisent précisément la structure algébrique voulue. En outre, lemoduleet l'argumentdeviennent respectivement le rapport et une mesure de l'angle de la similitude.
Il faut cependant vérifier que l'ensemble de ces matrices, complété par la matrice nulle, eststablepar produit:
ce qui justifie au passage lacommutativitédu produit et assure l'isomorphisme entre cette structure etcelle définie précédemment.
L'ensemble des réels s'identifie alors à l'ensemble des matrices diagonales de la forme
- ,
l'unité étant représentée par la matrice identité. L'élémentdésigne classiquement la matrice.
Ledéterminantcorrespond au carré dumodule,ce qui entraîne que tous les éléments non nuls sont inversibles et laméthode des cofacteursdémontre la stabilité par inverse.
Ce point de vue fournit une construction naturelle qui peut être adaptée pour obtenir l'algèbre réelle desquaternions.Il donne en outre une interprétation géométrique de la multiplication des nombres complexes comme composition desimilitudesdu plan. La conjugaison est enfin représentée par la transposition des matrices.
Classe d'équivalence de polynômes[modifier|modifier le code]
Un nombre complexe peut enfin être vu comme unpolynômeréel d'indéterminéei,où le carréi2est identifié avec le polynôme constant de valeur –1, donc avec les identificationsi3= –i,i4= 1…
Formellement, cela revient à assimiler l'ensemble des nombres complexes à l'anneau quotientℝ[X]/(X2+ 1), dans lequel deux polynômes appartiennent à la mêmeclasse d'équivalencesi et seulement s'ils ont le même reste dedivision euclidienneparX2+ 1.Cette construction justifie l'écriture d'un nombre complexe sous la formea+ ib,le polynômebX+apouvant s'obtenir comme le reste de la division euclidienne d'un polynôme parX2+ 1.
Le caractèreirréductibledu polynômeX2+ 1assure directement la structure de corps. Les réels sont représentés par les polynômes constants et le degré 2 du polynôme diviseur est la dimension de l'ensemble comme espace vectoriel réel.
Cette conception correspond à l'invention des nombres complexes,iayant été introduit comme l'une des racines de l'équationX2+ 1 = 0.Elle est loin de la géométrie et nécessite un seul générateur algébrique et une seule relation. Le formalisme, plus récent, du quotient d'unanneau euclidien,ici l'anneau des polynômes réels à une indéterminée, par un de sesidéaux premiersest à la base de la construction desextensions algébriquesde corps.
Développements en mathématiques[modifier|modifier le code]
Analyse complexe[modifier|modifier le code]
Les nombres complexes ont initialement été conçus pour répondre à un problème algébrique. Cependant, étendre les définitions de l'analyse au champ des nombres complexes s'avère tout aussi fécond. Par exemple la définition usuelle de la dérivée:(avec usage de la multiplication et de la soustraction complexes) permet d'obtenir une nouvelle notion de fonction dérivable, de variable complexe à valeurs complexes appeléefonction holomorphe.Cette notion s'avère plus restrictive que son pendant réel, notamment, toute fonction holomorphe voit sa dérivée être holomorphe, et même, toute fonction holomorphe estanalytique,c'est-à-dire admet undéveloppement en série entièreen chacun des points de son domaine d'holomorphie.
En théorie de l'intégration, en utilisant la notion d'intégrale le long d'un chemin, on obtient lethéorème intégral de Cauchy,qui assure que l'intégrale d'une fonction holomorphe, sur un domaine vérifiant certaines propriétés topologiques, le long d'un chemin fermé, est nulle. Cette propriété cruciale permet d'obtenir la notion de primitive d'une fonction holomorphe, toujours sur un domaine adapté. Certaines de ces conditions topologiques peuvent être abandonnées, grâce à la notion depoint singulier,aboutissant authéorème des résidus.
Dynamique holomorphe[modifier|modifier le code]
La dynamique holomorphe à une variable consiste en l'étude du comportement des itérés d'une fonction holomorphefdéfinie sur unesurface de Riemann.On distingue deux types de points sur ces surfaces: ceux où la famille des itérés estnormale,en ces points la dynamique est assez simple (bassins d'attractions de cycles de points périodiques), dont l'ensemble est appeléensemble de Fatoudef,puis ceux où le comportement estchaotiqueet dont l'ensemble est appeléensemble de Juliadef.
Les propriétés de ces itérés sont particulièrement bien connues dans le cadre de lasphère de Riemann:classification complète des composantes connexes de l'ensemble de Fatou selon les propriétés def,propriétés de l'ensemble de Julia, étude desfamilles paramétrées(en)de polynômes…
On étudie aussi la dynamique holomorphe à plusieurs variables, par exemple dans les espaces projectifs complexes où apparaissent de nouvelles difficultés par rapport à une variable telles que la présence d'ensembles de points oùfn'est pas définie.
Équations différentielles dans le champ complexe[modifier|modifier le code]
L'étude deséquations différentielles holomorphesa les mêmes résultats de base que celle des équations sur des fonctions de variable réelle, et notamment lethéorème de Cauchy-Lipschitz,qui donne l'existence et l'unicité d'une solution à un problème de Cauchy; ou les résultats d'algèbre linéaire sur les espaces de solutions des équations différentielles linéaires.
Cependant, l'étude des équations aux points singuliers est nettement plus féconde que les simples études de raccord du cas réel: la topologie du plan complexe au voisinage d'un point singulier fait qu'il y a une infinité de manières de l'approcher, et l'étude des raccords des solutions obtenues avec toutes les méthodes d'approche amène à la notion demonodromie.Cette notion est ensuite utilisée dans un cadre plus général: lathéorie de Galois différentielle.
Analyse de Fourier[modifier|modifier le code]
Nombres hypercomplexes[modifier|modifier le code]
Le corpsdes nombres complexes peut-être vu comme un sous-corps ou une sous-algèbre d’un corps ou d’une algèbre plus grande, dont les éléments sont alors qualifiés d’hypercomplexes.Par exemple,le corps non commutatif desquaternions,ou,l’algèbre à division,ni commutative ni associative, desoctonions.
En topologie[modifier|modifier le code]
- En identifiant l'espace vectoriel ℝ2navec l'espace vectoriel ℂn,la multiplication paridéfinit une application sanspoint fixesur lessphèresde dimension impaire.
- L'adjonction d'un «point à l'infini» au plan complexe définit lasphère de Riemannhoméomorphe à la sphère usuelle S2,qui peut être vue comme le premierespace projectifcomplexe.
La projection de la sphère S3,vue comme sphère unité de l'espace ℂ2,sur la sphère de Riemann par quotient de l'action ducercle unitéS1constitue alors lafibration de Hopf.
- Les espaces projectifs complexes de dimension paire engendrent rationnellement l'anneau decobordismeorienté[6].
Emploi en physique et ingénierie[modifier|modifier le code]
Phénomènes périodiques et analyse de Fourier[modifier|modifier le code]
La forme trigonométrique a permis de simplifier la modélisation et l’écriture de nombreux phénomènes, par exemple les phénomènes ondulatoires notamment à propos desondes électromagnétiques,ou enélectroniqueet plus précisément dans le domaine de l'analyse électronique des circuits contenant des auto-inductances (selfs ou bobines) notées L, des capacités notées C et des résistances notées R (exemples: R + jLω ou R – j/(Cω))[b].On peut tracer alors le diagramme de Fresnel, et ce quelle que soit l'expression.
En fait, on se sert du fait que ℂ contient ℝ pour simplifier les écritures. En effet, si l’on doit écrire qu’un paramètre vautrcos(θ), il faut deux réels,ret θ. Mais avec des complexes, il suffit d’un seul nombre, ce qui est bien plus simple.
Électromagnétisme[modifier|modifier le code]
Enélectromagnétismetoujours, mais dans un contexte différent, on peut écrire le champ électromagnétique comme une combinaison complexe du champ électrique et du champ magnétique. Pur artifice de calcul, on peut associer l'un ou l'autre de ces champs à la partie « imaginaire » du champ complexe obtenu: cela simplifie grandement les opérations.

Un autre exemple en électromagnétisme est lecourant alternatif:puisque levoltaged'un tel circuitoscille,il peut être représenté comme un nombre complexe via laformule d'Euler:
Afin d'obtenir une quantité mesurable, on prend la partie réelle[c]:
Analyse de Fourier[modifier|modifier le code]
On emploie également les complexes pour l'analyse de Fourier,très utilisée dans de nombreux domaines, comme le traitement du signal. L'idée sous-jacente à l'introduction des séries de Fourier est de pouvoir obtenir une fonction admettantTpour période, par exemple continue, comme somme de fonctions sinusoïdales:
avec les coefficientscn(f), appeléscoefficients de Fourierdef,définis par la formule:
Mécanique des fluides dans le plan[modifier|modifier le code]
Enmécanique des fluides(hydro/aérodynamique), on fait apparaître des potentiels[Quoi?]et des vitesses complexes. En effet, pour un écoulement à deux dimensions, on peut décomposer la vitesse du fluide enVxetVy.Or, on montre que:
Satisfaire à ces conditions (conditions deCauchy-Riemann) équivaut à dire qu'il existe une fonction analytique telle que
où
Ceci permet encore d’écrire:
On appellef(z) lepotentiel complexe,et sa dérivée par rapport àz,lavitesse complexe.Grâce à cette fonction, on obtient directement le module de la vitesse, et sa direction (en prenant la forme trigonométrique). Surtout, on peut modéliser simplement un écoulement autour d'un obstacle, d'une manière simple et compacte. La fonction ψ doit être constante le long du profil de cet obstacle, ce qui permet une résolution simple def,grâce à des résultats simples d’analyse complexe.
Fonction de structure[modifier|modifier le code]
Toujours dans l'analyse des phénomènes vibratoires, les propriétés des nombres complexes permettent non seulement de simplifier les calculs, mais aussi de déterminer des caractéristiques physiques d'un système oscillant, voire des propriétés fondamentales comme lacausalité[7].Unefonction de structureest une certaine fonction complexeoùest la fréquence complexifiée, la partie réelle étant la fréquence au sens usuel et la partie imaginaire représentant un facteur d'amortissementdu phénomène oscillant.
Les valeurs complexes deoùdiverge et tend vers l'infini sont nommés lespôlesde.Il s'avère qu'un pôle qui est d'un point de vue mathématique unesingularité,possède un sens physique et représente une fréquence derésonancedu système. De plus, l'étude de l'analyticité(en analyse complexe, il s'agit de l'holomorphicité) de la fonction de structure permet de connaitre des relations de causalité et savoir si un phénomène dépend d'excitations extérieures ou intrinsèques[7].
Il est possible également de définir une autre fonction de structure complexe,où t est untemps complexe.L'analyticité depermet cette fois-ci d’analyser les propriétés destabilitéd'un système physique et les conditions de retour à un état d'équilibre[7].
L'efficience et le pouvoir prédictif physique des fonctions de structure fait dire àMarc Lachièze-Reyque l'usage des nombres complexes dépasse le simple artifice de calcul et donne aux nombres complexes un degré de "réalité" physique comparable à celui des nombres réels[7].
Mécanique quantique[modifier|modifier le code]
Les nombres complexes sont omniprésents et indispensables à lamécanique quantique.Celle-ci est décrite dans desespaces vectoriels de Hilbertauxscalairescomplexes, et dont les vecteurs représentent desétats quantiques.Leur évolution est régie par l'équation de Schrödingerqui fait également intervenir des nombres complexes. Unegrandeur physiqueest représentée par uneobservablequi est uneapplication linéaired'un espace de Hilbert dans lui-même.
Laprojectiondu vecteur représentant l'état quantique sur un desvecteurs propresde cette observable donne une réalisation possible d'un état physique (une position donnée, une énergie donnée, etc.), et on quitte le domaine des nombres complexes en calculant la probabilité de réalisation de cet état physique, donnée par lemodule complexeau carré du vecteur projeté.
Lafonction de structurecomplexe (voir ci-dessus) joue également un grand rôle en physique quantique, car pardualité onde corpusculetout phénomène quantique se réduit à des phénomènes vibratoires ou oscillants. Ici, c'est l'énergied'un système qui est complexifiée avec la fréquence, via larelation de Planck-Einstein.Les pôles des fonctions de structure quantiques correspondent également à des phénomènes physiques essentiels comme l'apparition de nouvellesparticules élémentaireslors de collisions, et l'analyticité permet également d'exprimer une forme de causalité sous-jacente aux phénomènes quantiques[7].
SelonRoger Penrose,les propriétés mathématiques fondamentales des nombres complexes sous-tendent la physique duprincipe de superpositionet de l'équation de Schrödingeret les conditions de quantification d'un champ physique dans lathéorie quantique des champs,ce qui lui fait apparaître les nombres complexes comme étant un des fondements de la physique, avec les principes desymétrie[8].De son point de vue, la théorie quantique ne va pas assez loin dans le rôle fondamental donné aux nombres complexes car la théorie n'est totalementholomorphequ'avec des conditions arbitraires d'hermiticitédes opérateurs quantiques, et d'orthogonalité des résultats de mesure[8].Penrose va tenter de construire une théorie degravité quantiqueentièrement fondée sur les propriétés des nombres complexes et entièrement holomorphe: lathéorie des twisteurs.
En janvier 2021, Miguel Navascués et ses collègues de l'Institut d'optique quantique et d'information quantique deViennemontrent par un raisonnement théorique que les nombres complexes sont indispensables à la mécanique quantique, pas seulement des outils commodes comme pour la représentation des phénomènes périodiques, par exemple. Ils proposent aussi un test expérimental permettant d'exclure les théories quantiques à valeurs réelles. Deux groupes de recherche mènent ensuite l'expérience et confirment cette prédiction théorique[9],[10],[11],[12].
Relativité restreinte[modifier|modifier le code]
Gravité et cosmologie quantique[modifier|modifier le code]

Pour résoudre le problème de lasingularitéqui selon le modèle duBig Bangest à l'origine de l'univers,Stephen HawkingetJames Hartleont proposé une hypothèse d'ununivers sans bords,où la singularité initiale serait absente. Cette hypothèse repose sur l'idée que le temps, près de l'origine, est untemps imaginaire.Ce temps imaginaire permet de transformer lamétrique lorentzienneusuelle de l'univers(métrique de l'espace de Minkowski) enmétrique riemanniennedéfinie positive, ou pseudo-euclidienne,[13].
Le pari de Hawking et Hartle est que ce temps imaginaire permet de décrire lafonction d'ondecorrecte de l'univers et sa véritable physique aux alentours du Big Bang, donnée par la somme desintégrales de chemincalculées dans cette métrique où elles sont convergentes (tandis qu'elles sont divergentes et inexploitables en métrique lorentzienne). Cette fonction d'onde décrit la région de l'espace-temps du Big Bang comme unesuperposition quantiqued'espaces sans singularité semblables à une surface sphérique à 4 dimensions, où — comme la surface d'une sphère normale — la courbure est partout finie et varie continument, et où on peut évoluer sans rencontrer de « bords »[13],[14].
Contrairement à larotation de Wickqui n'est qu'une astuce de calcul, si l'hypothèse de Hartle-Hawking est correcte elle signifie que la nature physique du temps change à l'approche du Big Bang et devient une dimension semblable à une dimension d'espace[14].
Historique[modifier|modifier le code]
La première apparition d'une racine carrée de nombre négatif conçue comme une quantité impossible mais manipulable se trouve dans l’œuvre deCardanen 1545. Mais c'estRaphaël Bombelliqui étudie ces quantités sophistiquées de manière rigoureuse en 1572 dans sonAlgebra,ce qui en fait selon Flament le créateur indiscutable des nombres complexes[15].C'est également Bombelli qui les utilise pour la résolution de l'équation de degré 3.
Les nombres complexes interviennent dans l’œuvre d'Albert Girardquand il tente de démontrer que toute équation de degrénpossèdenracines vers 1629. Ils sont appelés sophistiqués, impossibles ou inexplicables jusqu'àRené Descartesqui les qualifie de quantités imaginaires en 1637. Ce qualificatif va leur rester jusqu'en 1831 où Gauss les appelle pour la première fois complexes.
Pour de nombreux mathématiciens duXVIIesiècle,écrire des quantités imaginaires, c'est s'autoriser l'utilisation des racines carrées de nombres négatifs, mais peu à peu se dégage une écriture normalisée sous la forme.Les mathématiciens tentent d'appliquer à ces nouvelles quantités les fonctions qu'ils connaissaient pour les quantités réelles en utilisant un principe de permanence[d].Somme, produit, quotient ne posent pas de problème, mais la racinen-ième se révèle une fonction non univoque.Abraham de Moivredémontre en 1738 l'égalité:
L'exponentiellene pose pas de problème. Ainsi, dès 1748, Euler écrit saformule
Mais la fonctionlogarithme complexerésiste longtemps àJean BernoullietGottfried Wilhelm Leibniz;c'estLeonhard Eulerqui les départage en 1749, en démontrant qu'elle prend une infinité de valeurs en un complexe donné[17].
C'est à Euler également que l'on doit la notation i pour√-1en 1777. Mais c'est surtoutCarl Friedrich Gaussqui en popularise l'usage. Le qualificatif d'«unité imaginaire» lui a été attribué par Gauss qui la qualifie ensuite d'« unité latérale », tandis queJean-Robert Argandlui préfère le terme d'« unité moyenne »[18]etWilliam Rowan Hamiltoncelui d'« unité secondaire ».
L'association entre complexes et vecteurs ou points du plan est l’œuvre de nombreux mathématiciens dontCaspar Wessel,Argand et Gauss à la fin duXVIIIesiècleet dans la première moitié duXIXesiècle.L'interprétation d'un complexe comme couple de réels muni d'une multiplication spéciale est l’œuvre d'Hamilton en 1833. L'interprétation d'un complexe comme reste moduloX2+ 1d'un polynôme à coefficient réel est l’œuvre d'Augustin Louis Cauchyen 1847. C'est également à Cauchy que l'on doit le développement de lathéorie des fonctions de la variable complexe[19].
L'utilisation en physique apparait dès le début duXIXesiècledans l’œuvre d'Augustin Fresnel(1823) dans son mémoire sur les lois de réflexion. En électricité,Arthur Edwin Kennelly,dès 1893, montre comment on peut facilement généraliser laloi d'Ohmau courant alternatif grâce aux complexes[20].
| Terme ou notation | Signification | Auteur | Date |
|---|---|---|---|
| ℞. m. 15 | Un nombreimpossibledont le carré vaudrait −15[e] | Cardan | 1545 |
| « Imaginaire » | Toute quantité contenant la racine carrée d'un nombre négatif | Descartes | 1637 |
| i | Euler | 1777 | |
| Module | Le module du complexea+ ibest | Argand | 1806 |
| Module dez(ou valeur absolue dez) | Karl Weierstrass | ||
| Conjugué | Le conjugué dea+ ibesta– ib | Cauchy | 1821 |
| Nombre complexe | a+ ib | Gauss | 1831 |
| Imaginaire pur | ib | ||
| « Norme » | Carré du module | ||
| Argument du complexez | Angle entre le vecteur associé à 1 et celui associé àz | Cauchy | 1838 |
| Affixe | L'affixe du point A de coordonnéesest le complexea+ ib | 1847 |
Les complexes dans les œuvres de fiction[modifier|modifier le code]
Dans le livreLes Désarrois de l'élève TörlessparRobert Musilet dans le film réalisé parVolker Schlöndorff(1966), Törless exprime devant le conseil de discipline de l'école sa difficulté à saisir le concept.
Notes et références[modifier|modifier le code]
Notes[modifier|modifier le code]
- Le nombreiest normalement représenté par un caractèreromain,l'italiqueétant réservé aux noms devariables.
- En électricité et en électronique, l'unité imaginaireest généralement notéejau lieu dei,pour éviter le risque de confusion entreieti,symbole habituel de l'intensité d'un courant électrique. Il existe par ailleurs un nombre complexe, fréquemment notéjen mathématiques, qui correspond à l'unique racine cubique de 1 dont la partie imaginaire est positive.
- Voir des exemples dans:Electromagnetism(2eédition), I.S. Grant, W.R. Phillips, Manchester Physics Series, 2008(ISBN0-471-92712-0)
- Principe consistant à généraliser aux complexes les propriétés connues sur l'ensemble des réels[16].
- Cette quantité sera par la suite notée.
Références[modifier|modifier le code]
- (en)Alan Sultan et Alice F. Artzt,The mathematics that every secondary school math teacher needs to know,Studies in Mathematical Thinking and Learning, Taylor & Francis, 2010,p. 326
- Jean Dieudonné,Calcul infinitésimal,Hermann,(ISBN978-2-7056-5907-3,OCLC6787042),p.24.
- «Programme de l'enseignement optionnel de mathématiques expertes de la classe terminale de la voie générale»,Bulletin officielspécial,no8,(lire en ligne,consulté le).
- (en)Hans Lundmark, «Visualizing complex analytic functions using domain coloring», (Représentation de fonctions analytiques complexes en utilisant la coloration de régions) Lundmark se réfère à Farris pour l'invention du terme "domain coloring",(consulté le)
- Flament 2003,chap. IV section 3, en particulier p. 386 et p. 413
- (en)J. W. MilnoretJ. D. Stasheff,Characteristic classes,Annals of Math. Studies76,Priceton University Press (1974)
- Jacques Bros et Marc Lachièze-Rey, encadré "De l'usage des nombres complexes en physique",p. 55 Sciences et Avenir n°138 Avril-Mai 2004
- Roger Penrose,A la découverte des lois de l'univers,2007, Ed. Odile Jacob, 34.8
- .
- (en)Johanna L. Miller, «Does quantum mechanics need imaginary numbers?»,Physics Today,vol.75,no3,,p.14(DOI10.1063/PT.3.4955,lire en ligne
 ,consulté le).
,consulté le).
- (en)Zheng-Da Li, Ya-Li Mao, Mirjam Weilenmann, Armin Tavakoli, Hu Chenet al.,«Testing Real Quantum Theory in an Optical Quantum Network»,Physical Review Letters,vol.128,,articleno040402(DOI10.1103/PhysRevLett.128.040402).
- (en)Ming-Cheng Chen, Can Wang, Feng-Ming Liu, Jian-Wen Wang, Chong Yinget al.,«Ruling Out Real-Valued Standard Formalism of Quantum Theory»,Physical Review Letters,vol.128,,articleno040403(DOI10.1103/PhysRevLett.128.040403).
- Roger Penrose,À la découverte des lois de l'univers,2007, Éd. Odile Jacob, 28.9.
- Modèle de Hartle-Hawking, Futura-Sciences.
- Flament 2003,p.24
- (Study et Cartan 1908,p.334)
- Communication d'Euler à l'académie des sciences de Berlin (en français, document PDF)
- Flament 2003,p.177
- DahanPeiffer,p.233
- Friedelmeyer 1998,p.312.
Voir aussi[modifier|modifier le code]
Bibliographie[modifier|modifier le code]
- A.Dahan-DalmedicoetJ. Peiffer,Une histoire des mathématiques: Routes et dédales,[détail des éditions]
- DominiqueFlament,Histoire des nombres complexes: Entre algèbre et géométrie,Paris, CNRS Éditions,(ISBN2 271 06128 8)
- Jean-PierreFriedelmeyer,« Le point de vue vectoriel, son application à la physique »,dansImages, Imaginaires, Imaginations - Une perspective historique pour l'introduction de nombres complexes,
- Jean-Denis Eiden,Géométrie analytiqueclassique, Calvage & Mounet, 2009,(ISBN978-2-91-635208-4)
- E.StudyetÉ.Cartan,« Les nombres complexes »,dansEncy. Sci. Math.,vol.1,t.1,(lire en ligne)
Articles connexes[modifier|modifier le code]
Liens externes[modifier|modifier le code]
- Notices dans des dictionnaires ou encyclopédies généralistes:
- Nombres complexes,G. Villemin
- J.-R. Argand,Essai sur une manière de représenter des quantités imaginaires dans les constructions géométriques,1806, en ligne et commenté par l'historien des sciencesC. Gérini, sur le sitebibnum
- Vidéo sur les complexes (série de 9 épisodes sur la représentation des dimensions dans l'espace),Étienne Ghys

















![{\displaystyle z^{n}=[r(\cos \theta +{\rm {i}}\sin \theta )]^{n}=r^{n}(\cos n\theta +{\rm {i}}\sin n\theta ).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60cb746faad76ba4f9270ea7e2da64822bc1396e)























![{\displaystyle \mathrm {Re} (V)=\mathrm {Re} \left[V_{0}{\rm {e}}^{{\rm {i}}\omega t}\right]=V_{0}\cos \omega t.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e33990c0e17d5962226323ef0a8f4a4cc7c5e88)










































