Courbe plane

Courbe hyperbolique.

Enmathématiques,plus précisément engéométrie,unecourbe planeest unecourbequi est entièrement contenue dans un (unique)plan,et qui est identifiable à unefonction continue:

$\ Alpha:I\longrightarrow \mathbb {R} ^{2}~$

où$I$est unintervallede l'ensemble$\mathbb {R}$desnombres réels.

L'imaged'une courbe est aussi appeléesupportde la courbe. Parfois, on utilise aussi l'expressioncourbepour indiquer le support d'une courbe. Unecourbesur unespace euclidiende dimension supérieure à 2 est diteplanesi son support est contenu dans un plan lui-même contenu dans l'espace euclidien dans lequel elle est définie.

Une courbe plane est ditesimplesi elle ne se recoupe pas, autrement dit, si

$\forall \ (t_{1},t_{2})\in I^{2},t_{1}\neq t_{2}\Longrightarrow \ Alpha (t_{1})\neq \ Alpha (t_{2})$.

Représentations

Représentation par une forme cartésienne explicite

Une manière de représenter une courbe plane est l'équation:

$y=f(x)\,$

telle qu'à chaque pointxcorresponde un pointy,et de façon que chaque point du planxy:(x,y)représente le support de la courbe. Une courbe de ce type est également nommée graphique en référence au graphique d'une fonction réelle; en effet, la représentation peut aussi s'écrire:

$\ Alpha (t)=(t,f(t))\,$

c'est-à-dire comme fonction d'unevariable indépendante.Cette représentation a de nombreuses limites géométriques, du fait que très souvent, une courbe a une description très complexe sous cette forme, qui n'est donc pas adaptée à l'étude des propriétés géométriques.

Représentation par une forme cartésienne implicite

Une courbe peut également être représentée sous la forme:

$F(x,y)=0\,$

c'est-à-dire comme fonction de deuxvariables indépendantes.Cette représentation est, selon certains points de vue, meilleure que la représentation explicite; cependant, on peut rencontrer des problèmes quand il faut expliciter l'une des deux variables en fonction de l'autre: souvent, c'est très compliqué, quand ce n'est pas impossible.

Représentation paramétrée

La meilleure représentation est sans aucun doute la représentation paramétrée, du type:

$\ Alpha:{\begin{cases}x=\phi (t)\\y=\psi (t)\end{cases}}$ou bien$\ Alpha (t)=(\phi (t),\psi (t))$

où$t\in I$s'appelle leparamètre.

La condition de continuité ne suffit pas pour représenter et étudier les courbes vues comme objets filiformes à une dimension avec les caractéristiques de régularité voulues. La condition supplémentaire est que la courbe plane soitdifférentiablesur$I$.

Une courbe plane paramétrée$\ Alpha (t)=(\phi (t),\psi (t))$est dite différentiable en tout point si les fonctions$\phi (t)$et$\psi (t)$ont des dérivées continues en tout point.

On dit qu'une courbe plane paramétrée estrégulièreen un point$t_{0}$(ou que$t_{0}$est unpoint régulierpour cette courbe) si$\ Alpha '(t_{0})=(\phi '(t_{0}),\psi '(t_{0}))\neq (0,0)$;elle est dite régulière sur I si$\ Alpha '(t)\neq (0,0)$en tout point$t$de$I$.

Un point$t_{0}$tel que$\ Alpha '(t_{0})=(0,0)$est appelé pointsingulierpour la courbe.

Tangente

Tangente en un point d'une courbe

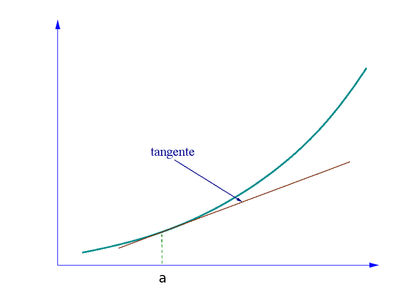
La régularité de la courbe permet de définir la droitetangenteà la courbe. Soient$\ Alpha (t)$une courbe différentiable et$P_{0}=\ Alpha (t_{0})$un point régulier. On peut définir la tangente à la courbe en ce point comme étant la droite passant par$P_{0}$et parallèle auvecteur$\ Alpha '(t_{0})=(\phi '(t_{0}),\psi '(t_{0}))$.

La tangente a uneéquation cartésienneau point$t_{0}$:

$\psi '(t_{0})\cdot (X-\phi (t_{0}))-\phi '(t_{0})\cdot (Y-\psi (t_{0}))=0$

et pour équations paramétrées:

${\begin{cases}X_{t}=\phi '(t_{0})(t-t_{0})+\phi (t_{0})\\Y_{t}=\psi '(t_{0})(t-t_{0})+\psi (t_{0})\end{cases}}$

Dans le cas d'une courbe représentée explicitement par une équation$y=f(x)$,la tangente au point$(x_{0},y_{0})$est donnée par la relation:

$f'(x_{0})\cdot (x-x_{0})-(y-y_{0})=0$.

Dans le cas d'une courbe représentée par une équation implicite$F(x,y)=0$,la tangente au point$(x_{0},y_{0})$est donnée par la relation:

$F_{x_{0}}\cdot (x-x_{0})+F_{y_{0}}\cdot (y-y_{0})=0$

où$F_{x_{0}}$(respectivement$F_{y_{0}}$) désigne ladérivée partiellepar rapport à$x$(respectivement$y$) de$F$,évaluée au point$x_{0}$(respectivement$y_{0}$).

Normale

La régularité de la courbe permet de définir la droitenormaleà la courbe au point$t_{0}$,d'équation cartésienne:

$\phi '(t_{0})\cdot (\phi (t_{0})-\phi (t))+\psi '(t_{0})\cdot (\psi (t_{0})-\psi (t))=0$.

Cette équation devient, avec les mêmes notations que dans le paragraphe précédent:

• Pour une représentation explicite:

$f'(x_{0})\cdot (y-y_{0})+(x-x_{0})=0$.

• Pour une représentation implicite:

$F_{y_{0}}\cdot (x-x_{0})-F_{x_{0}}\cdot (y-y_{0})=0$.

Cosinus directeurs

D'après la définition même de ladérivée,on obtient:

${\frac {\psi '(t)}{\phi '(t)}}=\tan \theta$

ce qui, d'un point de vue géométrique, représente la pente de la droite tangente à la courbe, autrement dit latangente(au sens trigonométrique du terme) de l'angle que cette tangente forme avec l'axe horizontal (l'axe des 'x'). De cette relation, on peut extraire les cosinus directeurs de la tangente à la courbe:

$\cos \theta =\pm {\frac {\phi '(t)}{\sqrt {\phi '(t)^{2}+\psi '(t)^{2}}}}$

$\sin \theta =\pm {\frac {\psi '(t)}{\sqrt {\phi '(t)^{2}+\psi '(t)^{2}}}}$

Reparamétrage

Soient$\ Alpha:I\longrightarrow \mathbb {R} ^{2}$une courbe plane différentiable, et$t=t(s)$une fonction définie sur l'intervalle$S$et à valeurs dans$I$.Alors la courbe:

$\beta =\ Alpha \circ t:S\longrightarrow \mathbb {R} ^{2},$

telle que pour tout$s\in S,\beta (s)=\ Alpha (t(s))$,est un reparamétrage de la courbe$\ Alpha$.Le reparamétrage est dit régulier si$t(S)=I$et si$\forall s\in S,t'(s)\neq 0$.

On vérifie alors le théorème suivant: si$\beta =\ Alpha \circ t$est un reparamétrage de la courbe$\ Alpha$par$t=t(s)$alors

$\beta '(s)={\frac {dt}{ds}}\ Alpha '(t(s))$

Démonstration

Si$\ Alpha (t)=(\phi (t),\psi (t))$alors$\beta (s)=(\phi (t(s)),\psi (t(s)))$et d'après les théorèmes de dérivation des fonctions composées, on a:

${\frac {d\phi (t(s))}{ds}}={\frac {d\phi }{dt}}\cdot {\frac {dt}{ds}}$

${\frac {d\psi (t(s))}{ds}}={\frac {d\psi }{dt}}\cdot {\frac {dt}{ds}}$

et ainsi on obtient:

$\beta '(s)={\frac {dt}{ds}}\left({\frac {d\phi }{dt}},{\frac {d\psi }{dt}}\right)={\frac {dt}{ds}}\ Alpha '(t(s))$

Longueur d'une courbe

Longueur d'un arc paramétré

Soient$\ Alpha (t)=(\phi (t),\psi (t))$une courbe différentiable sur I, et$[a,b]\subseteq I$.Alors la longueur de l'arc de courbe compris entre$\ Alpha (a)$et$\ Alpha (b)$vaut:

$L(\ Alpha )=\int _{a}^{b}\|\ Alpha '(t)\|dt=\int _{a}^{b}{\sqrt {\phi '(t)^{2}+\psi '(t)^{2}}}\cdot dt$.

Si de plus$\beta (s)$est un reparamétrage de la courbe, alors:

$L(\ Alpha )=L(\beta )=\int _{a}^{b}\|\ Alpha '(t)\|dt=\int _{a}^{b}\|\beta '(s)\|ds$.

Longueur et forme cartésienne explicite

Si la courbe est représentée sous forme cartésienne explicite$y=f(x)$alors, comme${\frac {dx}{dx}}=1$et${\frac {df(x)}{dx}}={\frac {dy}{dx}}$,la longueur de la courbe est donnée par:

$L=\int _{a}^{b}{{\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}}\cdot dx}$.

Paramétrage avec les coordonnées polaires planes

Une forme de paramétrage qui revêt une importance notable dans l'étude des mathématiques, de la géométrie et dans de nombreux domaines d'application des mathématiques, est celle descoordonnées polaires planes.Étant donné une courbe paramétrée en coordonnées polaires par la forme cartésienne$r=r(\theta )$,avec c ≤ θ ≤ d, et par la forme paramétrée:

${\begin{cases}\phi (\theta )=r(\theta )\cos \theta \\\psi (\theta )=r(\theta )\sin \theta \end{cases}}$,de paramètre θ.

Alors ses dérivées sont:${\begin{cases}\phi '(\theta )=r'(\theta )\cos \theta -r(\theta )\sin \theta \\\psi '(\theta )=r'(\theta )\sin \theta +r(\theta )\cos \theta \end{cases}}$

et donc la longueur de l'arc est:

$L=\int _{c}^{d}{{\sqrt {\phi '(\theta )^{2}+\psi '(\theta )^{2}}}\cdot d\theta }=\int _{c}^{d}{{\sqrt {r(\theta )^{2}+r'(\theta )^{2}}}\cdot d\theta }=\int _{c}^{d}{{\sqrt {r(\theta )^{2}+\left({\frac {dy}{dx}}\right)^{2}}}\cdot d\theta }$.

Abscisse curviligne

On définit l'abscisse curviligneouparamètre longueur d'arccomme étant le reparamétrage particulier obtenu en fixant la borne inférieure d'intégrationa,de façon que l'intégrale$s(t)=\int _{a}^{t}{\|\ Alpha '(u)\|du}$ne dépende que de la borne supérieuret,vue comme variable. Cette fonction est, géométriquement, la longueur de l'arc de courbe à partir d'un point fixea,affectée éventuellement d'un signe. Il est toujours possible de paramétrer de nouveau la courbe selon l'abscisse curviligne. Dans ce cas, pour déterminer la tangente en un point, on sait qu'elle est parallèle à un vecteur tangent unitaire. On démontre que l'on peut toujours paramétrer de nouveau une courbe au moyen de l'abscisse curviligne de la façon suivante:

étant donné que$s'(t)=\|\ Alpha '(t)\|>0$,on peut inverser$s(t)$,et son inverse est$t=t(s)$.Alors on obtient le reparamétrage par l'abscisse curviligne donné par:$\beta (s)=\ Alpha (t(s))$.

On démontre ensuite que le vecteur tangent est unitaire:

$\|\beta '(s)\|=|{\frac {dt}{ds}}|\cdot \|\ Alpha '(t)\|={\frac {1}{|s'(t)|}}\|\ Alpha '(t)\|={\frac {\|\ Alpha '(t)\|}{\|\ Alpha '(t)\|}}=1$.

Courbure

Soit$\beta (s)$une courbe paramétrée selon l'abscisse curviligne et$\beta '(s)$son vecteur tangent unitaire. Considérons la fonction$k:S\longrightarrow \mathbb {R},s\longmapsto k(s)=\|\beta ''(s)\|$.Alors la fonction$k(s)\geq 0$est ditecourburede la courbe.

Si la courbe est représentée explicitement, sa courbure est:

$k={\frac {f''(x)}{\left(1+f'^{2}\right)^{3/2}}}$.

En revanche, pour une courbe représentée par une équation implicite, la courbure est évaluée par:

$k={\frac {F_{y}^{2}\cdot F_{xx}-2F_{x}\cdot F_{y}\cdot F_{xy}+F_{x}^{2}\cdot F_{yy}}{\left(F_{x}^{2}+F_{y}^{2}\right)^{3/2}}}$.

Formules de Frenet

Une courbe (suffisamment régulière) de l'espace pos sắc de, en tous ses points, un système de référence, dittrièdre de Frenet,donné par un triplet de vecteurstangent,normaletbinormal.Une telle courbe est plane si et seulement si le vecteur binormal est toujours nul.

Soit$\beta (s)=(\phi (s),\psi (s))$une courbe paramétrée selon l'abscisse curviligne. Le vecteur unitaire tangent est déterminé par:

$T(s)=\beta '(s)=(\phi '(s),\psi '(s)).$

Le vecteur unitaire normal est déterminé par:

$N(s)=\mathrm {i} \cdot T(s)=(-\psi '(s),\phi '(s)),$

oùiest l'unité imaginairetelle que$\mathrm {i} ^{2}=-1$.Grâce à la définition de la courbure, on peut donner une autre forme au vecteur unitaire normal:

$N(s)={\frac {T'(s)}{\|T'(s)\|}}={\frac {T'(s)}{k(s)}}.$

On démontre que le vecteur$T'$est orthogonal àTet donc parallèle àN.

Finalement, lesformules de Frenetet lacourburepour une courbe plane, quel que soit son paramétrage$\ Alpha (t)=(\phi (t),\psi (t))$,sont:

$T(t)={\frac {\ Alpha '(t)}{\|\ Alpha '(t)\|}}$

$N(t)={\frac {\mathrm {i} \cdot \ Alpha '(t)}{\|\ Alpha '(t)\|}}$

$k(t)={\frac {\ Alpha ''(t)\cdot (\mathrm {i} \ Alpha '(t))}{\|\ Alpha '(t)\|^{3}}}$

Exemples de courbes planes

Courbes planes classiques

• Ladroite

• Lecercle
  • Lecercle unité

• lescissoïdes:
  • Lacissoïde de Dioclès
  • Laconchoïde de Sluze

• Lesconiques:
  • l'ellipse
  • laparabole
  • l'hyperbole

• lescourbes cycloïdales:
  • lacycloïde
  • l'épicycloïde
  • l'hypocycloïde
  • lacardioïde
  • lanéphroïde
  • l'astroïde
  • ladeltoïde

• Les courbesisochrones:
  • L'isochrone de Huygens
  • L'isochrone de Leibniz
  • L'isochrone paracentrique
  • L'isochrone de Varignon

• leslemniscates:
  • Lelemniscate de Bernoulli
  • Lelemniscate de Gerono
  • Lelemniscate de Booth

• Lesspirales:
  • Laspirale d'Archimède
  • Laspirale hyperbolique
  • Laspirale logarithmique
  • Laspirale de Fermat
  • Laclothoïdeou spirale d'Euler
  • Laspirale de Cotes
  • Laspirale de Galilée
  • Lelituus

• lasinusoïde
• lafonction exponentielle
• l'atriphtaloïde(en)
• lachaînette
• Lefolium de Descartes
• l'hélice
• lesconchoïdes
• lelimaçon de Pascal
• Lespétales de rose
• Lastrophoïde
• Lasuperellipse
• latractrice
• Latrisectrice de Maclaurin
• lacourbe du chien

• les courbesenveloppes
• lescourbes développantes

Constructions

• Lacourbe du dragon
• Leflocon de Koch
• Lescourbes de Bézier
• Lessplines
• courbe de largeur constante

Courbes analytiques

• Courbe fermée
• Courbe rectifiable
• Courbe de Jordan
• Courbe de Peano
• Courbe de Sierpinski

Courbes algébriques

Unecourbe algébriqueest unevariété algébriquededimension(en)1, généralement exprimée sous la forme d'unpolynômede degré divers. Des exemples incluent:

• Lesdroites projectives
• Les courbes quadriques, autre nom desconiques,de degré 2
• Lescourbes cubiques,de degré 3
  • La cubique d'Agnesi
• Lescourbes quartiques,de degré 4
  • Lacourbe de Klein
• Lescourbes quintiques,de degré 5
  • Laquintique de l'Hospital
• Lescourbes sextiques,de degré 6
• Lescourbes elliptiques
• Lescourbes hyperelliptiques
• Lescourbes modulaires
• Lescourbes de Fermat

Voir aussi

Articles connexes

• Courbe
• Différentielle
• Dérivée
• Géométrie différentielle classique

Références

• (it)Cet article est partiellement ou en totalité issu de l’article de Wikipédia en italien intitulé«Curva piana»(voir la liste des auteurs).

Liens externes

• (fr)Mathcurve:une encyclopédie des courbes