Format virgule flottante demi-précision
Eninformatique,le formatdemi-précision(appelé parfoisFP16oufloat16) est unformat de nombre(en)binaireenvirgule flottantequi occupe16 bits(deuxoctetssur les ordinateurs modernes) enmémoire de l'ordinateur.Elle est conçue pour le stockage de valeurs en virgule flottante dans des applications où une précision supérieure n'est pas essentielle, en particulier dans letraitement d'imageset lesréseaux de neurones.
Presque toutes les utilisations modernes suivent la normeIEEE 754-2008,où le format enbase 2sur 16 bits est appelébinary16,et l'exposant utilise 5 bits. Elle peut représenter des valeurs sur la plage ± 65504, la plus petite valeur supérieure à 1 étant 1 + 1/1024.
En fonction de l'ordinateur, la demi-précision peut être plus rapide d'au moins un ordre de grandeur que la double précision, par exemple 550 PFLOPS pour la demi-précision contre 37 PFLOPS pour la double précision sur un serveur du cloud[1].
Historique
[modifier|modifier le code]Plusieurs formats en virgule flottante 16 bits ont existé dont celui du DSP HD61810 d'Hitachi en 1982 (un exposant de 4 bits et une mantisse de 12 bits)[2],le WIF de Thomas J. Scott en 1991 (5 bits d'exposant, 10 bits de mantisse)[3]et leprocesseur graphique Voodoo de 3dfxde 1995 (identique à Hitachi)[4].
ILMrecherchait unformat d'imagequi pourrait accepter une largegamme dynamique,mais sans la lourdeur et le coût mémoire du format à virgule flottante simple ou double précision[5].Le groupeshading programmable accéléré par hardwaredirigé par John Airey àSGI (Silicon Graphics)inventa le type de données s10e5 en 1997 dans le cadre du travail de conception 'bali'. Ceci est décrit dans un article présenté àSIGGRAPH2000[6](voir section 4.3) et documenté plus à fond dans le brevet US 7518615[7].Il a été popularisé pour son usage dans le format d'image open-sourceOpenEXR.
NvidiaetMicrosoftont défini letypehalf(demi) dans lelangage Cg,publié début 2002, et implémenté dans lesiliciumdans la carte graphiqueGeForce FX,sortie fin 2002[8].Depuis lors, le support des nombres à virgule flottante 16 bits est devenu très courant sur les cartes graphiques.
L'extensionF16C(en)sortie en 2012 permet aux processeursx86de convertir des flottants demi-précision en flottants simple précision et vice-versa en une instruction machine.
Format virgule flottante binaire demi-précision de l'IEEE 754: binary16
[modifier|modifier le code]La norme IEEE 754[9]spécifie unbinary16comme ayant le format suivant:
- Bit de signe:1 bit
- Largeur de l'exposant:5 bits
- Précisionde lamantisse:11 bits (10 explicitement stockés)
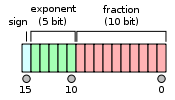
Le format est organisé comme suit:
Dans ce format, la mantisse est réputé avoir un bit de poids fort implicite de valeur 1, sauf si le champ de l'exposant ne contient que des zéros. Par conséquent, seuls 10 bits de lamantisseapparaissent dans le format mémoire mais la précision totale est de 11 bits. En termes IEEE 754, la mantisse fait 10 bits, mais la précision de la mantisse est de 11 bits (log10(211) ≈ 3,311 chiffres décimaux, soit 4 chiffres ± légèrement moins que 5unité de plus faible précision(en).
Codage de l'exposant
[modifier|modifier le code]L'exposant du nombre format binaire en virgule flottante demi-précision est codé avec une représentationbinaire décalée,le décalage du zéro étant de 15; appelée égalementexposant biaisédans la norme IEEE 754.
- Emin= 000012− 011112= −14
- Emax= 111102− 011112= 15
- Exposant biaisé = 011112= 15
Par conséquent, comme défini par la représentation binaire biaisée, afin d'obtenir le vrai exposant le biais de 15 doit être soustrait de l'exposant stocké.
Les exposants stockés 000002et 111112sont interprétés spécialement.
| Exposant | Mantisse = zéro | Mantisse ≠ zéro | Équation |
|---|---|---|---|
| 000002 | zéro,−0 | nombres dénormalisés | (−1)bits de signe× 2−14× 0.bits de la mantisse2 |
| 000012,..., 111102 | valeur normalisée | (−1)bits de signe× 2exposant−15× 1.bits de la mantisse2 | |
| 111112 | ±infini | NaN(silencieux, avertisseur) | |
La plus petite valeur strictement positive (dénormalisée) est 2−24≈ 5.96 × 10−8. La plus petite valeur positive normalisée est 2−14≈ 6.10 × 10−5. La plus grande valeur représentable est (2−2−10) × 215= 65504.
Exemples de nombres demi-précision
[modifier|modifier le code]Ces exemples sont donnés en représentation binaire de la valeur en virgule flottante. Elle comprend le bit de signe, l'exposant (biaisé) et la mantisse.
| Binaire | Hex | Valeur | Notes |
|---|---|---|---|
| 0 00000 0000000000 | 0000 | 0 | |
| 0 00000 0000000001 | 0001 | 2−14× (0 +11024) ≈ 0.000000059604645 | plus petit nombre positif dénormalisé |
| 0 00000 1111111111 | 03ff | 2−14× (0 +10231024) ≈ 0.000060975552 | plus grand nombre dénormalisé |
| 0 00001 0000000000 | 0400 | 2−14× (1 +01024) ≈ 0.00006103515625 | plus petit nombre positif normalisé |
| 0 01101 0101010101 | 3555 | 2−2× (1 +3411024) ≈ 0.33325195 | valeur la plus proche de 1/3 |
| 0 01110 1111111111 | 3bff | 2−1× (1 +10231024) ≈ 0.99951172 | plus grand nombre inférieur à un |
| 0 01111 0000000000 | 3c00 | 20× (1 +01024) = 1 | un |
| 0 01111 0000000001 | 3c01 | 20× (1 +11024) ≈ 1.00097656 | plus petit nombre supérieur à un |
| 0 11110 1111111111 | 7bff | 215× (1 +10231024) = 65504 | plus grand nombre normal |
| 0 11111 0000000000 | 7c00 | ∞ | infini |
| 1 00000 0000000000 | 8000 | −0 | |
| 1 10000 0000000000 | c000 | −2 | |
| 1 11111 0000000000 | fc00 | −∞ | infini négatif |
Par défaut, 1/3 est arrondi en valeur inférieure comme endouble précision,à cause du nombre impair de bits dans la mantisse. Les bits au-delà du point d'arrondi sont0101... ce qui inférieur à 1/2unité de plus faible précision(en).
Références
[modifier|modifier le code]- (en)«About ABCI - About ABCI | ABCI», surabci.ai(consulté le)
- (en)«hitachi:: dataBooks:: HD61810 Digital Signal Processor Users Manual», surArchive.org(consulté le)
- (en)Thomas J.Scott,Proceedings of the twenty-second SIGCSE technical symposium on Computer science education - SIGCSE '91,vol.23,,130–139p.(ISBN0897913779,DOI10.1145/107004.107029
 ,S2CID16648394),« Mathematics and computer science at odds over real numbers »
,S2CID16648394),« Mathematics and computer science at odds over real numbers »
- (en)«/home/usr/bk/glide/docs2.3.1/GLIDEPGM.DOC», surGamers.org(consulté le)
- «OpenEXR», OpenEXR(consulté le)
- (en)Mark S. Peercy, Marc Olano, John Airey et P. Jeffrey Ungar, «Interactive Multi-Pass Programmable Shading», surPeople.csail.mit.edu(consulté le)
- (en)«Patent US7518615 - Display system having floating point rasterization and floating point... - Google Patents», surGoogle(consulté le)
- (en)«vs_2_sw», surCg 3.1 Toolkit Documentation,Nvidia(consulté le)
- (en)IEEE Standard for Floating-Point Arithmetic,IEEE STD 754-2019 (Revision of IEEE 754-2008),,1–84p.(ISBN978-1-5044-5924-2,DOI10.1109/ieeestd.2019.8766229,lire en ligne)