Parabole

Une parabole représentée par la fonction f(x)=x².

Laparaboleest unecourbe plane,symétriquepar rapport à unaxe,ayant approximativement la forme d'un U dont les branches s'écarteraient indéfiniment. Cette courbe intervient dans les problèmes les plus élémentaires de mécanique ou de mathématiques. En effet latrajectoire d'un projectilequi n'est soumis qu'à lapesanteurest une parabole, ou encore, en mathématiques, la représentation graphique despolynômesde degré 2 est une parabole.

La parabole peut se définirmathématiquementde plusieurs façons, équivalentes. Le plus souvent, la parabole est définie comme une courbe plane dont chacun des points est situé à égale distance d'unpoint fixe,lefoyer,et d'une droite fixe, ladirectrice.Mais on peut aussi la définir comme l'intersection d'unplanavec uncône de révolutionlorsque le plan estparallèleavec un autreplan tangentà lasurfacedu cône.

Son nom, parabole (juxtaposition, similitude), lui a été donné parApollonius de Perge,remarquant, dans sa construction, une égalité d'aireentre unrectangleet uncarré.

Il s'agit d'un type decourbe algébriquedont les nombreuses propriétés géométriques ont intéressé lesmathématiciensdès l'Antiquitéet ont reçu des applications techniques variées enoptique,télécommunication,etc.

Section conique

Les paraboles font partie de la famille desconiques,c'est-à-dire des courbes qui s'obtiennent par l'intersection d'uncônede révolution avec un plan; en l'occurrence, la parabole est obtenue lorsque le plan est parallèle à l'une des génératrices du cône et perpendiculaire à l'autre plan qui contient la même génératrice et l'axe du cône.

La parabole est l'intersection d'un plan avec un cône de révolution lorsque le plan est parallèle à une des génératrices du cône.

Directrice, foyer et excentricité

Parabole de droite directricedet de foyerF.

SoientDune droite etFun point n'appartenant pas àD,et soit$P$le plan contenant la droiteDet le pointF.On appelle parabole dedroite directriceDet defoyerFl'ensemble des points$M$du plan$P$à égaledistancedu foyerFet de la droiteD,c'est-à-dire vérifiant:

$d(M,F)=d(M,D)$

où$d(M,F)$mesure la distance du pointMau pointFet$d(M,D)$mesure la distance du pointMà la droiteD.La parabole est une forme deconiquedont l'excentricité$e$vaut 1.

Paramètre

Égalité de l'aire du rectangle bleu de hauteur fixe 2p et du carré rouge dans une parabole.

Dans sesConiques,Apollonius de Pergeexhibe un paramètre permettant de caractériser les points de la parabole à l'aide de l'égalité d'un carré et d'un rectangle de hauteur fixecorrespondant au double de ce que l'on nomme actuellement leparamètrep de la conique. Si S est le sommet de la parabole d'axe (S,x), M un point de la parabole, N son projeté sur l'axe de la parabole, alors l'aire du carré de côté MN est égale à l'aire du rectangle de dimensions SN et 2p. Remarquant que, dans le cas de l'hyperbole, l'aire du carré est plus grande que celle du rectangle et que dans le cas de l'ellipse, cette aire est plus petite, c'est lui qui donne le nom à ces trois courbes: parabole (juxtaposition, similitude) dans le cas de l'égalité, hyperbole (appliqué avec excès) dans le cas où le carré est plus grand que le rectangle et ellipse (appliqué avec défaut) dans le cas où le carré est plus petit que le rectangle.

Équations

À partir du foyer et de la directrice

Si la parabole est donnée par son foyerFet sa directrice${\mathcal {D}}$,on appelleKle projeté orthogonal deFsur${\mathcal {D}}$,on appellep(paramètre de la parabole) la distanceFKet l'on appelleSle milieu de[FK].Alors, dans le repère orthonormé$(S,{\vec {i}},{\vec {j}})$où${\vec {j}}$a même direction et sens que${\overrightarrow {KF}}$,l'équation de la parabole est

$y={\frac {x^{2}}{2p}}$

À partir de la fonction du second degré

Dans un repère orthonormal, la courbe représentative d'unefonction polynomialedu second degré d'équation

$y=ax^{2}+bx+c$

oùa,betcsont des constantes réelles (anon nul), est une parabole. Dans le casa= 1,b = c= 0,on obtient une expression simple pour une parabole

$y=x^{2}$.

Dans le repère orthonormal$(O,{\vec {i}},{\vec {j}})$,le sommetSd'une parabole est le point de coordonnées$\left(-{\tfrac {b}{2a}},-{\tfrac {b^{2}-4ac}{4a}}\right)$.Son axe de symétrie est l'axe$(S{\vec {j}})$.

Dans le repère orthonormal$(S,{\vec {i}},{\vec {j}})$,son équation est$Y=aX^{2},$Son foyer est le point$F\left(0;{\tfrac {1}{4a}}\right)$et sa directrice est la droite${\mathcal {D}}$d'équation$Y=-{\frac {1}{4a}}$.

Dans le repère orthonormal$(O,{\vec {i}},{\vec {j}})$,le foyer a donc pour coordonnées$\left(-{\frac {b}{2a}},{\frac {1-\Delta }{4a}}\right)$et la directrice pour équation$y=-{\frac {1+\Delta }{4a}}$où$\Delta =b^{2}-4ac$.

Démonstration

Dans le repère orthonormal$(S,{\vec {i}},{\vec {j}})$,on considère

$F\left(0;{\tfrac {1}{4a}}\right)$

${\mathcal {D}}:Y=-{\frac {1}{4a}}$.

SoitM(X,Y).Le repère étant orthonormal, on calcule directement la distanceddu pointMà la droite${\mathcal {D}}$:

$\mathrm {d} =\left|Y+{\frac {1}{4a}}\right|$

De même, le repère étant orthonormal, on calcule la distanced' =FM:

$\mathrm {d} '={\sqrt {\left(Y-{\frac {1}{4a}}\right)^{2}+X^{2}}}$.

On interprète, par équivalence, la conditiond = d'

$\mathrm {d} =\mathrm {d} '\Longleftrightarrow \mathrm {d} ^{2}=\mathrm {d} '^{2}\Longleftrightarrow \left(Y+{\frac {1}{4a}}\right)^{2}=\left(Y-{\frac {1}{4a}}\right)^{2}+X^{2}$

$\mathrm {d} =\mathrm {d} '\Longleftrightarrow {\dfrac {Y}{a}}=X^{2}\Longleftrightarrow Y=aX^{2}$

donc

$\mathrm {d} =\mathrm {d} '\Longleftrightarrow M\in {\mathcal {P}}:Y=aX^{2}$.

À partir de l'équation générale

Soit l'équationAx²+ 2Bxy+Cy²+ 2Dx+ 2Ey+F= 0,dans un repère orthonormal. SiB²-AC= 0alors cette équation est celle d'une parabole ou de deux droites parallèles.

Réciproquement, si (C) est une parabole, alors elle pos sắc de, dans tout repère orthonormal, une équation de la forme précédente.

Soit l'équationAx²+Cy²+ 2Dx+ 2Ey+F= 0,dans un repère orthonormal. SiAC= 0avecAEouDCnon nul alors cette équation est celle d'une parabole dont l'axe est parallèle à un des axes du repère.

Projection du rayon vecteur sur l'axe.

L'équation$y=ax^{2}+bx+c$($a\neq 0$) dans un repère quelconque est toujours l'équation d'une parabole. Son axe de symétrie n'est pas parallèle à l'axe des$y$si le repère n'est pas orthogonal.

Équation polaire

Si l'on prend comme pôle le foyerFde la parabole et comme axe polaire l'axe focal dirigé vers la directrice, par projection sur l'axe, il vientr + rcos (θ) =p.

On en déduit que l'équation polairede la parabole est${\overrightarrow {r}}={\overrightarrow {FP}}={\frac {p}{1+\cos(\theta )}}{\vec {e}}_{\theta }$que l'on reconnaît comme un cas particulier deconiqued'excentricitée= 1.

Paramétrisation

Dans le repère cartésien$(S,{\vec {i}},{\vec {j}})$oùSest le point situé au milieu du segment constitué du foyerFet de sa projectionKsur la directrice et où${\vec {j}}$est unvecteur unitaireorienté deSversF,on peut envisager plusieursparamétrisationsde la parabole:

1. Une paramétrisationcartésiennepar l'abscisse:${\overrightarrow {SP}}(x)=x{\vec {i}}+{\frac {x^{2}}{2p}}{\vec {j}}$,pour tout$x\in \mathbb {R}$;
2. Une paramétrisation cartésienne par l'ordonnée:${\overrightarrow {SP}}(y)=(\pm {\sqrt {2py}}){\vec {i}}+y{\vec {j}}$,pour tout$y\in \mathbb {R} ^{+}$;
3. Des paramétrisations cartésiennes dépendant chacune d'un constante arbitrairea> 0:${\overrightarrow {SP}}(t)=2pat{\vec {i}}+2pa^{2}t^{2}{\vec {j}}=2pa(t{\vec {i}}+at^{2}{\vec {j}})$,pour tout$t\in \mathbb {R}$.

(Poura= 1/(2p), on retrouve la paramétrisation par l'abscisse.) Ces paramétrisations sont régulières (c.-à-d.levecteur dérivéne s'annule pas). Le vecteur(1, 2at)dirige alors latangenteau point de paramètret.

Quelques propriétés géométriques de la parabole

Cordes parallèles

Diamètre de la parabole relatif à la directionD'.

Toutes les cordes de la parabole parallèles à une même droiteD'ont leur milieu situé sur une même droiteDparallèle à l'axe: c'est undiamètrerelatif à la directionD'.Les deux tangentes à la parabole aux extrémités d'une telle corde se coupent enD.La tangente à la parabole parallèle àD'a son point de contact surD.

Tangente et bissectrice

SiAest un point sur une parabole définie par un foyerFet une directrice (d), alors la tangente de la parabole enAest labissectriceintérieure (b) de l'angle formée parF,Aet le projeté orthogonal deAsur (d).

Démonstration

(b) est la tangente enAet la bissectrice de l'angle (FAH).

SoitHle projeté orthogonal deAsur (d), (b) la bissectrice de l'angle FÂH.

On sait que la parabole découpe le plan en deux zones: l'une, contenantF,regroupe les pointsMpour lesquels FM < FM_Het l'autre, contenant (d), regroupe les pointsMpour lesquels FM > FM_H.On montre que (b) est la tangente en A à la parabole en prouvant qu'elle est entièrement incluse (excepté le point A) dans la zone vérifiant FM > FM_H.

Le triangleFAHest isocèle enApar définition de la parabole. Donc (b) est aussi la médiatrice de[FH].

Soit A' un point sur (b) distinct de A. A' appartient donc à la médiatrice de [FH] et A'F = A'H.

Soit H' le projeté orthogonal de A' sur (d). Le triangle HH'A' est rectangle en H' donc A'H' < A'H.

Donc finalement A'H' < A'F. Donc A' est dans la partie du plan vérifiant FM > FM_H.

La droite (b) est entièrement incluse dans cette zone (sauf au point A), c'est donc la tangente à la parabole en A.

Une démonstration purement analytique est possible. Dans le repère$(S,{\vec {i}},{\vec {j}})$,l'équation de la parabole est:

$y=ax^{2}$

La tangente au point d'abscissema pour vecteur directeur

${\vec {u}}(1,2am)$

Les points F et H ont pour coordonnées respectives

$F\left(0,{\frac {1}{4a}}\right)$et$H\left(m,-{\frac {1}{4a}}\right))$

La droite (HF) a pour vecteur directeur

${\vec {v}}\left(m,-{\frac {1}{2a}}\right)$

elle est donc orthogonale à la tangente, puisque${\vec {u}}\cdot {\vec {v}}=1\times m+2am\times (-{\frac {1}{2a}})=0$.

La tangente est donc hauteur du triangle isocèle AFH, c'est donc bien la bissectrice de l'angle FÂH.

Illustration de la propriété en optique.

Cette propriété explique le principe des miroirs paraboliques: l'angle que font les droites (AF) et (b) est égal à l'angle que font les droites (AH) et (b), donc les droites (AH) et (AF) sont symétriques par rapport à la tangente, ainsi que par rapport à la normale à la tangente. En optique, cela signifie qu'un rayon issu de F et frappant A subit uneréflexion spéculairede direction (AH), puisque selon laloi de Snell-Descartes,l'angle d'incidence est égal à l'angle de réflexion. Donc, tous les rayons issus de F sont réfléchis dans la même direction, perpendiculaire à (d).

Propriété relative à l'orthoptique

Lorsque l'on se déplace le long de sa directrice, la parabole est toujours vue sous un angle droit.

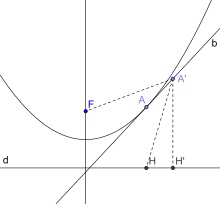
SoientMetM'les points d'intersection d'une droite quelconque passant par le foyer de la parabole avec la parabole. Les deux tangentes de la parabole passant parMetM'se coupent sur la directrice en formant un angle droit entre elles. De plus, si l'on appelleHetH'les projetés respectifs deMetM'sur la directrice etOle point d'intersection des deux tangentes et de la directrice, alorsOest le milieu de[HH'].

Lorsque l'on se déplace le long de sa directrice, la parabole est toujours vue sous un angle droit.

Démonstration

On noteOle point d'intersection des deux tangentes. Pour des notations plus simples des angles, on note

$\ Alpha ={\widehat {FMO}}$et$\beta ={\widehat {FM'O}}$.

D'après la corrélation montrée plus haut entre tangente et bissectrice, on a:

${\widehat {FMH}}=2\ Alpha$

${\widehat {FM'H'}}=2\beta$

Puisque les droites (HM) et (H'M') sont parallèles, les deux angles précédents, découpés par (MM') sur ces droites, sont supplémentaires. On a donc:

$2\beta +2\ Alpha =\pi \Leftrightarrow \beta +\ Alpha ={\frac {\pi }{2}}$

On en déduit directement avec la somme des angles d'un triangle:

${\widehat {MOM'}}=\pi -\left(\ Alpha +\beta \right)={\frac {\pi }{2}}$

On appellePle point d'intersection de la perpendiculaire à(MM')passant parFavec la directrice. Les triangles FMP et HMP sontégauxcarFM = HMdonc le pointPest sur la bissectrice de l'angle FMH, il est donc sur la tangente passant parM;de même, le pointPest sur la tangente passant parM'.Le pointPest donc aussi le pointOd'intersection des deux tangentes qui se trouve donc bien sur la directrice.

Les deux tangentes se coupent donc en angle droit sur la directrice.

Enfin, les égalitésFP = HPetFP = H'Pprouvent quePdoncOest le milieu de[HH'].

En prenant deux tangentes perpendiculaires pour axes, l'équation prend alors la forme remarquable:${\sqrt {{x} \over {a}}}+{\sqrt {y \over b}}-1=0$

où(a,0)et(0,b)sont les nouvelles coordonnées des points de contact.

Sous-normale constante

Les triangles sont égaux, leurs bases sont constantes.

D'un pointMde la courbe, on mène la normale qui coupe l'axeΔenN,soitHle projeté orthogonal deMsurΔ.La valeurHNs’appelle la sous-normale. On montre qu'elle admet comme valeur constantep,le paramètre de la parabole.

Démonstration

La pente de la tangente étant$y'=\tan \theta$,le triangle rectangleMHNdonne${\overline {HN}}=PH\times \tan \theta =yy'$.

Or, si l'on dérive par rapport àxl'équation de la paraboley²– 2px= 0,on obtient précisémentyy' = p.

Applications

Balistique

Trajectoire parabolique.

Trajectoire d'une balle de basket.

Laparaboleestla trajectoiredécrite par un objet qu'on lance, si l'on peut négliger la courbure de laTerre,lefrottement de l'air(vent, ralentissement de l'objet par sa traînéeaérodynamique) et la variation de lagravitéavec la hauteur.

Torricellia démontré en1640que l'enveloppede ces trajectoires est elle-même une parabole:parabole de sûreté.

Comparaison de la forme d'un jet d'eau avec la parabole.

Dans la pratique, cependant, la trajectoire d'un objet projeté dans l'air (balle de sport, balle de fusil, obus) est très différente d'une parabole, du fait de la traînée atmosphérique, ce qui complique énormément les calculs des balisticiens. Un cas particulier est la courbe décrite par un jet d'eau (image ci-contre) puisque, si ce jet d'eau est bien régulier, seules des forces de friction atmosphériques freinent les parois du jet (il n'y a pas de traînée de pression): or la traînée de friction est d'un ordre de grandeur beaucoup plus faible que la traînée de pression (cette traînée de pression étant, par contre, très forte sur les projectiles comme les balles de sport).

Ondes hertziennes, acoustiques et lumineuses

Parmétonymie,uneparaboledésigne uneantenne parabolique.Il s'agit plus exactement d'une application des propriétés de la surface nomméeparaboloïde de révolution.

Principe du phare automobile à miroir parabolique.

Les paraboloïdes permettent de concentrer des ondes ou des rayons en un point, le foyer de la parabole. Cette propriété est utilisée par lesantennes paraboliquespour concentrer uneonde électromagnétique,par le réflecteur parabolique associé à unmicrophonepour concentrer desondes acoustiques,ou encore par certainsfours solairespour concentrer lalumière du soleil.

À l'inverse elles peuvent également diffuser sous forme d'un faisceau cylindrique la lumière produite par unelampeau foyer de la parabole. Cette propriété est exploitée par leprojecteuret lephare.

Une portion de cylindre de section parabolique permet, de même, de concentrer la lumière sur une droite, par exemple dans des concentrateurs solaires.

Littérature

Dans un des livres de Jules VerneDe la Terre à la Lune,la parabole est une forme hypothétique de la trajectoire de sa fusée pour atteindre la Lune.

Voir aussi

Articles connexes

• Coniques
  • Hyperbole
  • Ellipse
• Parabole semi-cubique
• Constante parabolique universelle

Liens externes

• Xavier Hubaut,Les théorèmes belges- Coniques et théorème de Dandelin
• Xavier Hubaut,Lancement du poids- Parabole de sûreté
• Bernard Vitrac, «Les géomètres de l'antiquité 8- Apollonius de Perge et la tradition des coniques», surcultureMATH (Ressources pour les enseignants de mathématiques, site expert desÉcoles normales supérieureset duministère de l'Éducation nationale)
• Parabole,sur le site MathCurve

Bibliographie

• Jean-Denis Eiden,Géométrie analytique classique,Calvage & Mounet, 2009(ISBN978-2-91-635208-4).
• Jean Fresnel,Méthodes modernes en géométrie.
• Bruno Ingrao,Coniques affines, euclidiennes et projectives,Calvage & Mounet,(ISBN978-2-916352-12-1).