Pentagone
| Pentagone | |
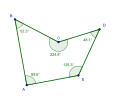
 Un pentagone concave et sesangles internes. | |
| Type | Polygone |
|---|---|
| Arêtes | 5 |
| Sommets | 5 |
| modifier |
|
Engéométrie,unpentagoneest unpolygoneàcinqsommets,donc cinq côtés et cinqdiagonales.
Un pentagone est soitsimple(convexe ou concave), soitcroisé.Lepentagone régulier étoiléest lepentagramme.
Étymologie
[modifier|modifier le code]Le terme « pentagone » dérive du latinpentagonumde même sens, substantivation de l'adjectifpentagonus,lui-même emprunté augrec ancien,πεντάγωνος(pentágônos), « pentagonal », « qui a cinq angles, cinq côtés »[1],[2].Le terme grec est lui-même construit à partir deπέντε(pénte), « cinq », etγωνία(gônía), « angle ».
Le terme grec apparaît dans lelivre IVdesÉlémentsd'Euclide,probablement écrit vers 300av. J.-C.,qui traite des figuresinscritesoucirconscrites,en particulier despolygones réguliers.
Généralités
[modifier|modifier le code]Pentagones quelconques
[modifier|modifier le code]Lasomme des angles internesd'un pentagonesimple(dont les arêtes ne se croisent pas) est égale à 540°.Cette égalité n'est pas vérifiée si le pentagone n'est pas simple.
-
Pentagone convexe quelconque
-
Pentagone concave quelconque
-
Pentagone concave dont l'un des sommets est lié aux quatre autres
-
Pentagone croisé quelconque
-
Pentagone convexeéquilatéral
-
Pentagone concave équilatéral
-
Pentagone convexeéquiangle
Pentagones inscriptibles
[modifier|modifier le code]Un pentagone inscriptible est un pentagone pour lequel existe uncercle circonscrit,passant par ses cinq sommets.
L'aired'un pentagone inscriptible peut être exprimée comme laracine carréede l'une desracinesd'uneéquation du septième degré(en)dont les coefficients sont fonction des côtés[3],[4],[5].
Un pentagone inscrit dont les arêtes et l'aire sont desnombres rationnelsest appelépentagone de Robbins(en).Les longueurs de ses diagonales sont soit toutes rationnelles, soit toutesirrationnelles;onconjecturequ'elles doivent être toutes rationnelles[6].
-
Pentagone inscriptible convexe quelconque et son cercle circonscrit.
-
Pentagone de Robbins, de côtés 26, 80, 72, 136 et 154, et d'aire 13 104.
Deux pentagones réguliers
[modifier|modifier le code]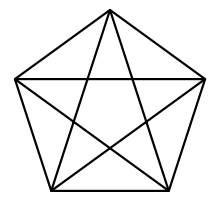

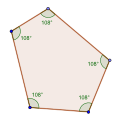
Un pentagonerégulierest un pentagone dont les cinqcôtés sont de même longueuret dont les cinqangles internessont de même mesure. Il en existe deux types:
- lepentagone régulier convexe,généralement appelé simplement « pentagone régulier »;
- le pentagone régulierétoilé,oupentagramme,en forme d'étoile à cinq branches.
Lesdiagonalesd'un pentagone régulier convexe de côtéaforment un pentagramme de côtéφa,oùφest lenombre d'or.
Il est possible de construire les deux pentagones réguliersà la règle et au compas.De nombreuses méthodes existent,l'une d'elles étant déjà connue d'Euclide auIIIesiècleav. J.-C.
Une méthode par pliage simple permet de construire un pentagone régulier: il suffit de prendre une bande de papier suffisamment longue, d'initier une boucle, d'y passer une extrémité et de serrer en ajustant[réf.souhaitée].

Usages
[modifier|modifier le code]Graphes
[modifier|modifier le code]Legraphe completK5est souvent dessiné sous forme d'un pentagramme inscrit dans un pentagone régulier convexe. Ce graphe représente également laprojection orthogonaledes 5 arêtes et 10 sommets dupentachore,unpolytoperégulier convexe en dimension quatre.
-
Projection orthogonale d'unpentachore
-
Projection orthogonale d'un5-cellules rectifié(en)
Pavages
[modifier|modifier le code]Il n'est pas possible depaverleplan euclidienpar des pentagones réguliers convexes. Il est en revanche possible de le paver par des pentagones quelconques. En 2015, on connait 15 types de pavages pentagonauxisoédriques,c'est-à-dire employant un même type de tuile. On ignore s'il en existe d'autres.
-
L'agencement le plus dense connu de pentagones réguliers convexes de même taille sur un plan est une structure couvrant 92,131 % de ce plan.
-
Les 15 pavages pentagonaux connus en 2015.
Polyèdres
[modifier|modifier le code]Il existe plusieurspolyèdresdont lesfacessont des pentagones:
- ledodécaèdre réguliercomporte 12 pentagones réguliers convexes; il s'agit d'unsolide de Platon;
- le pyritoèdre pos sắc de 12 faces pentagonales identiques, mais pas forcément régulières;
- l'icositétraèdre pentagonalest constitué de 24 faces pentagonales irrégulières; c'est unsolide de Catalan;
- l'hexacontaèdre pentagonal,comportant 60 faces pentagonales irrégulières; c'est également un solide de Catalan;
- letrapézoèdre tronqué(en),troncature d'untrapézoèdreà2nfaces, comporte2npentagones. Le trapézoèdre pentagonal tronqué, issu d'untrapézoèdre pentagonal,est entièrement constitué de 12 pentagones. S'il est régulier, c'est un dodécaèdre régulier.
-
Pyritoèdre
Références
[modifier|modifier le code]- Informationslexicographiquesetétymologiquesde « pentagone » dans leTrésor de la langue française informatisé,sur le site duCentre national de ressources textuelles et lexicales.
- (en)«πεντάγωνος», Perseus Digital Library.
- (en)Eric W. Weisstein,«Cyclic Pentagon», surMathWorld.
- (en)David P. Robbins, «Areas of Polygons Inscribed in a Circle»,Discrete & Computational Geometry,vol.12,no1,,p.223-236(DOI10.1007/BF02574377).
- (en)David P. Robbins, «Areas of Polygons Inscribed in a Circle»,American Mathematical Monthly,vol.102,no6,,p.523-530(DOI10.2307/2974766).
- (en)Ralph H.Buchholzet James A.MacDougall,«Cyclic polygons with rational sides and area»,Journal of Number Theory,vol.128,no1,,p.17–48(DOI10.1016/j.jnt.2007.05.005).
Voir aussi
[modifier|modifier le code]- Dodécaèdre,polyèdre dont la forme régulière convexe est constituée de 12 faces pentagonales
- Nombre pentagonal
- Table de lignes trigonométriques exactes