Integral

Nocálculo,aintegraldunhafunciónfoi creada orixinalmente para determinar aáreabaixo unhacurvanoplano cartesiano,mais tamén xorde naturalmente en ducias de problemas deFísica,como por exemplo na determinación daposiciónen todos os instantes dun obxecto, sendo coñecida a súavelocidadeen todos os instantes.

O proceso de calcular a integral dunha función chámaseintegración.

Diferentemente da noción asociada dederivación,existen varias definicións para a integración. Todas elas tratando de resolver algúns problemas conceptuais relacionadas con límites, continuidade e existencia de certos procesos utilizados na definición. Porén todas estas definicións dan a mesma resposta para o resultado final dunha integración.

Cando a integral é sobre un intervalo definido trátase dunhaintegral definida$\int _{a}^{b}f(x)dx=F(x){\bigg |}_{a}^{b}=F(b)-F(a)=S$,con resultado un valor numérico. Cando a integral non ten un intervalo definido chámaseantiderivada$\int _{}^{}f(x)dx=F(x)$,ouintegral indefinida,ouprimitiva,ouinversa da derivadacon resultado unha función.

Definición conceptual

Integrando a área dunha función abaixo dunha curva.

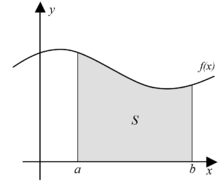
Para describir a integral dunha función f(x) dun intervalo x entre [a, b] utilízase a notación:

$S=\int _{a}^{b}f(x)dx$

A idea desta notación utilizando unSdado é xeneralizar a noción desumatorio.Isto porque intuitivamente a integral de$f(x)$pode ser entendida como a suma de pequenos rectángulos de base$dx$e altura$f(x)$,onde o produto$f(x)dx$é a área deste rectángulo. A suma de todas estas pequenas áreas, ou áreas infinitesimais, fornece a área total abaixo da curva. Máis precisamente pode dicirse que a integral de riba é o valor límite da suma:

$\sum _{i=0}^{N}f(x_{i})\Delta x.$

onde:

$\Delta x={\frac {b-a}{N}}$

é a lonxitude dos pequenos intervalos nos cales se divide o intervalo$[a,b]$,$f(x_{i})$é o valor da función nalgún punto deste intervalo. O que se espera é que cando$N$for moito grande o valor da suma se aproxime do valor da área debaixo da curva e, polo tanto, da integral de$f(x)$no intervalo. Ou sexa que o límite

$\lim _{N\to \infty }\sum _{i=0}^{N}f(x_{i})\Delta x=\int _{a}^{b}f(x)dx=S$

estea definido. O problema é que este raciocinio intuitivo é difícil de expresar en linguaxe matemática precisa. Por isto existen varias formas de definir a integración dun xeito formal. O resultado, no entanto, é coherente entre elas.

Teorema do valor medio do cálculo integral

Se$f$é unha función continua no intervalo$[a,b]$,entón existe un punto$c\in (a,b)$tal que$\int _{a}^{b}f(x)dx=(b-a)f(c)$.

Teorema fundamental do Cálculo

Teorema fundamental do cálculo Sexa f continua en$[a,b]$e$F(x)=\int _{a}^{x}f$a función integral definida para todo$x\in [a,b]$,daquela$F^{'}(x)=f(x)$.

A función procuradaF(x)é unha función tal que, ao tomar a súa derivada obtense a funciónf(x). Esta propiedade móstranos que a integración na verdade é a operación inversa da derivación, pois ao derivar unha función e deseguido a integrarmos, obterase a función orixinal.

Demostración

$F^{'}(x)=\lim _{h\to 0}{\dfrac {F(x+h)-F(x)}{h}}=\lim _{h\to 0}{\dfrac {\int _{a}^{x+h}f-\int _{a}^{x}f}{h}}=\lim _{h\to 0}{\dfrac {\int _{x}^{x+h}f}{h}}.$

Poloteorema do valor mediodo cálculo integral existe un punto$c_{h}\in (x,x+h)$tal que$\int _{x}^{x+h}f=hf(c_{h}).$

A maiores se$h\to 0$,entón$c_{h}\to x$e temos finalmente que

$\lim _{h\to 0}{\dfrac {hf(c_{h})}{h}}=\lim _{h\to 0}f(c_{h})=f(x).$

Demostración 2

Ao resolver a integral de riba entre os límitesaeb,o resultado final pódese escribir como:

$S=\int _{a}^{b}f(x)dx=F(b)-F(a)$

Onde a funciónF(x)é a función resultante da integración da funciónf(x).O problema da integración, isto é, atopar a solución para unha integral, resúmese polo tanto a atopar a funciónF(x).

Para ver isto, supoña que o límite superior da integral, isto é,bé moito próximo dea,tal que se poida escribir:

$b=a+\Delta x$

Como os puntos límites da integral están moito próximos pode escribirse:

$\int _{a}^{a+\Delta x}f(x)dx=F(a+\Delta x)-F(a)$

E ollando na definición da integración como un límite, dada arriba, pode dicirse que a integral, neste caso resúmese a só un dos termos na suma, e polo tanto pode dicirse, sen causar un erro moi grande, que:

$\int _{a}^{a+\Delta x}f(x)dx=f(a)\Delta x=F(a+\Delta x)-F(a)$

Comparando coa definición daderivadadunha función:

$f(x)={\frac {F(x+\Delta x)-F(x)}{\Delta x}}\rightarrow f(x)={\frac {d}{dx}}F(x)$

Exemplo de cálculo paso a paso para un polinomio

Calculando primeiro as primitivas (integral indefinida) e despois aplicando os valores do intervalo (integral definida).

Fórmula da primitiva para as potencias de x

$\int cx^{n}dx={\frac {cx^{n+1}}{n+1}}$

sendo$c$unha constante.

Exemplo cun polinomio:

$\int _{0}^{3}(x^{2}+2x+4)dx$

Trátase cada membro da función como unha función separada, e deseguido efectúase a suma entre eles e xérase outra función, a función na cal se substituirá o valor de X polos valores do intervalo; deste xeito, úsase o teorema do cálculo para chegar ao valor da integral.

Intervalo$(0,3).$

$f(x)=x^{2}+2x+4.$

$\int (x^{2})dx+\int (2x)dx+\int (4)dx.$

Aquí úsase a Fórmula da Primitiva para cada integral.

$F(x)={\frac {x^{2+1}}{2+1}}+{\frac {2x^{1+1}}{1+1}}+{\frac {4x^{0+1}}{0+1}}.$

Isto xera a función que se usará para substituír os valores do intervalo.

$F(x)={\frac {x^{3}}{3}}+x^{2}+4x$.

Para$x=0=a.$

$F(a)=0$

Para$x=3=b.$

$F(b)={\frac {3^{3}}{3}}+3^{2}+4\cdot 3=30$

TEOREMA FUNDAMENTAL DO CÁLCULO.

$\int _{a}^{b}f(x)dx=F(x){\bigg |}_{a}^{b}=F(b)-F(a)$

$\int _{0}^{3}(x^{2}+2x+4)dx={\frac {3^{3}}{3}}+3^{2}+12-0$

$\int _{0}^{3}(x^{2}+2x+4)dx=30$

Exemplos de integrais

Artigo principal:Lista de integrais.

Unha breve lista das integrais indefinidas máis frecuentes son

• Se${\mathrm {d} \over \mathrm {d} x}f(x)=g(x)$,daquela$\int g(x)\mathrm {d} x=f(x)+C$.
• $\int 1\ \mathrm {d} x=x+C$
• $\int a\ \mathrm {d} x=ax+C$
• $\int x^{n}\mathrm {d} x={\frac {x^{n+1}}{n+1}}+C;\ n\neq -1$
• $\int \sin {x}\ \mathrm {d} x=-\cos {x}+C$
• $\int \cos {x}\ \mathrm {d} x=\sin {x}+C$
• $\int \sec ^{2}{x}\ \mathrm {d} x=\tan {x}+C$
• $\int \csc ^{2}{x}\ \mathrm {d} x=-\cot {x}+C$
• $\int \sec {x}\tan {x}\ \mathrm {d} x=\sec {x}+C$
• $\int \csc {x}\cot {x}\ \mathrm {d} x=-\csc {x}+C$
• $\int {\frac {1}{x}}\ \mathrm {d} x=\ln |x|+C$
• $\int \mathrm {e} ^{x}\mathrm {d} x=\mathrm {e} ^{x}+C$
• $\int a^{x}\mathrm {d} x={\frac {a^{x}}{\ln a}}+C;\ a>0,\ a\neq 1$
• $\int {\frac {1}{\sqrt {a^{2}-x^{2}}}}\ \mathrm {d} x=\arcsin \left({\frac {x}{a}}\right)+C$
• $\int {\frac {1}{a^{2}+x^{2}}}\ \mathrm {d} x={\frac {1}{a}}\arctan \left({\frac {x}{a}}\right)+C$

E tres exemplos para obter a integral definida dadas as correspondentes primitivas:

$\int _{a}^{b}1dx=x|_{a}^{b}=b-a$(Integral da función constante f(x)=1)

$\int _{a}^{b}xdx={\frac {1}{2}}x^{2}|_{a}^{b}={\frac {1}{2}}(b^{2}-a^{2})$(Integral dunha función f(x) = x)

$\int _{0}^{\pi }\sin(x)\,dx=-\cos(x){\big |}_{x=0}^{x=\pi }=-\cos(\pi )-{\big (}-\cos(0){\big )}=2.$

Por definición, a barra$f(x)|_{a}^{b}$utilízase co significado da diferenza$f(b)-f(a)$

Definicións de integral

Hai moitas formas de definir formalmente unha integral, non todas son equivalentes. As diferenzas existen principalmente para tratar casos especiais diferentes que poden non ser integrábeis baixo outras definicións, mais tamén son ocasionalmente por razóns pedagóxicas. As definicións máis utilizadas son as deintegral de Riemanneintegral de Lebesgue.

Integral de Riemann

Artigo principal:Integral de Riemann.

Integral baixo o punto de visda das sumas de Riemann baseadas nunhapartición etiquetada,con posicións de mostraxe e anchos irregulares (máximo en vermello).

A integral de Riemann defínese en termos desumas de Riemannde funcións en relación ásparticións etiquetadasdun intervalo. Sexa [a,b] unintervalopechado da recta real; entón unhapartición etiquetadade [a,b] é unha secuencia finita:

$a=x_{0}\leq t_{1}\leq x_{1}\leq t_{2}\leq x_{2}\leq \cdots \leq x_{n-1}\leq t_{n}\leq x_{n}=b.\,\!$

Converxencia das sumas de Riemann como intervalos divididos, cando a mostraxe faise á■dereita,■o mínimo,■o máximo ou■a esquerda.

Isto divide o intervalo [a,b] en subintervalosi[x_i−1,x_i], onde cada un deles está "etiquetado" cun punto específicot_ide [x_i−1,x_i]. Sexa Δ_i=x_i−x_i−1o ancho do subintervaloi.Unhasuma de Riemanndunha funciónfen relación a esta partición etiquetada defínese como

$\sum _{i=1}^{n}f(t_{i})\Delta _{i};$

Así, cada termo da suma é a área do rectángulo cunha altura igual ao valor da función no punto especificado do subintervalo dado e do mesmo ancho que o ancho do subintervalo. O paso desta partición etiquetada é o ancho do maior subintervalo obtido pola partición, isto é, max_i=1…nΔ_i.Aintegral de Riemanndunha funciónfsobre o intervalo [a,b] é igual aSse:

Para todos os ε > 0 existe δ > 0 tal que, para calquera partición etiquetada [a,b] cun paso menor que δ, temos

$\left|S-\sum _{i=1}^{n}f(t_{i})\Delta _{i}\right|<\epsilon.$

Cando as etiquetas escollidas dan o valor máximo (ou mínimo) da función na integral respectiva, a suma de Riemann convértese nunhasuma de Darbouxsuperior (ou inferior), o que suxire a estreita conexión que existe entre a integral de Riemann. e aintegral de Darboux.

Integral de Lebesgue

Artigo principal:Integral de Lebesgue.

A integral de Riemann non está definida para unha ampla gama de funcións e situacións de importancia práctica (e de interese teórico). Por exemplo, a integral de Riemann pode integrar facilmente a densidade para obter a masa dunha trabe de aceiro, mais non se pode adaptar a unha bola de aceiro que descansa sobre ela. Isto motiva a creación doutras definicións, baixo as que se poden integrar unha variedade máis ampla de funcións.A integral de Lebesgue, en particular, alcanza unha gran flexibilidade baseada en centrar a atención nos pesos da suma ponderada.

Así, a definición da integral de Lebesgue comeza cunhamedida,μ. No caso máis sinxelo, amedida de Lebesgueμ(A) dun intervaloA= [a,b] é o seu ancho,b−a,polo que a integral de Lebesgue coincide coa integral de Riemann cando ambas as dúas existen. En casos máis complicados, os conxuntos que se van medir poden estar moi fragmentados, sen continuidade nin semellanza de intervalos.

Para sacar proveito desta flexibilidade, a integral de Lebesgue inverte o enfoque da suma ponderada. Como di Folland:"Para calcular a integral de Riemann def,o dominio [a,b] está dividido en subintervalos ", mentres que na integral de Lebesgue," de feito o que se está a dividir é o camiño def".

Un enfoque común é definir primeiro a integral dafunción característicadunconxunto medibleAcomo:

$\int 1_{A}d\mu =\mu (A)$.

Isto esténdese por linearidade a unhafunción en escadasimple, que só teñen un número finitonde valores distintos non negativos:

${\begin{aligned}\int s\,d\mu &{}=\int \left(\sum _{i=1}^{n}a_{i}1_{A_{i}}\right)d\mu \\&{}=\sum _{i=1}^{n}a_{i}\int 1_{A_{i}}\,d\mu \\&{}=\sum _{i=1}^{n}a_{i}\,\mu (A_{i})\end{aligned}}$

(onde a imaxe deA_icando se aplica a función en escadasé o valor constantea_{i</ sub>). Entón, seEé un conxunto medíbel, defínese}

$\int _{E}s\,d\mu =\sum _{i=1}^{n}a_{i}\,\mu (A_{i}\cap E).$

Entón, para calquerafunción mediblenon negativa defínesef

$\int _{E}f\,d\mu =\sup \left\{\int _{E}s\,d\mu \,\colon 0\leq s\leq f{\text{ e }}s{\mbox{ é unha función en escada}}\right\};$

É dicir, estabelécese que a integral defé osupremode todas as integrais de función en escada que son menores ou iguais af. Calquera función medíbel "f" sepárase entre os seus valores positivos e negativos en función da definición

${\begin{aligned}f^{+}(x)&{}={\begin{cases}f(x),&{\text{se }}f(x)>0\\0,&{\text{se non}}\end{cases}}\\f^{-}(x)&{}={\begin{cases}-f(x),&{\text{se }}f(x)<0\\0,&{\text{se non}}\end{cases}}\end{aligned}}$

Finalmente,fé Lebesgue integrábel se

$\int _{E}|f|\,d\mu <\infty,\,\!$

E entón a integral defínese por

$\int _{E}f\,d\mu =\int _{E}f^{+}\,d\mu -\int _{E}f^{-}\,d\mu.\,\!$

Cando o espazo métrico no que se definen as funcións tamén é unespazo topolóxicolocalmente compacto(como é o caso dos números reais ℝ), as medidas son compatíbeis coa topoloxía en certo sentido. apropiado (medida de Radon). Este é o enfoque adoptado porBourbakie un certo número doutros autores. Para máis detalles, consulteMedidas de Radon.

Outras definicións de integral

Aínda que as integrais de Riemann e Lebesgue son as definicións máis importantes dunha integral, hai algunhas outras, incluíndo:

• Aintegral de Riemann-Stieltjes,unha extensión da integral de Riemann.
• Aintegral de Lebesgue-Stieltjes,desenvolvida por Johann Radon, que xeneraliza as integrais de Riemann-Stieltjes e Lebesgue.
• Aintegral de Daniell,que inclúe a integral de Lebesgue e a integral de Lebesgue-Stieltjes sen necesidade de depender de ningunha medida.
• Aintegral de Henstock-Kurzwe,definida de varias maneiras por Arnaud Denjoy, Oskar Perron e (na forma máis elegante) Jaroslav Kurzweil, é desenvolvida porRalph Henstock.
• Aintegral de Darboux,que é equivalente á integral de Riemann.
• Aintegral de Haar,que é a integral de Lebesgue coamedida de Haar.

Propiedades da integral definida

• $\int _{a}^{b}(f(x)\pm g(x))dx=\int _{a}^{b}f(x)dx\pm \int _{a}^{b}g(x)dx.$
• $\int _{a}^{b}kf(x)dx=k\int _{a}^{b}f(x)dx.$
• Se$f(x)\geq 0\in [a,b]$,daquela$\int _{a}^{b}f(x)dx\geq 0.$
• $\int _{a}^{a}f(x)dx=0.$
• Se$f(x)\leq g(x)\in [a,b]$,daquela$\int _{a}^{b}f(x)dx\leq \int _{a}^{b}g(x)dx.$
• Se$c\in [a,b]$,temos$\int _{a}^{b}f(x)dx=\int _{a}^{c}f(x)dx+\int _{c}^{b}f(x)dx.$

Cálculo de integrais

Para calcular unha integral pódese buscar unhaprimitivada función e despois aplicar oteorema fundamental do cálculopara determinar o valor da integral.

Pódese tentar automatizar esta técnica usando programas informáticos que implementen algoritmos deintegración simbólica.Non sempre é posible atopar a primitiva dunha función e ás veces, aínda que sexa posible, o resultado é moi complexo.

Outra forma de atopar un valor aproximado da integral é utilizar o que se chamacadratura numérica,que é un conxunto de algoritmos que permiten calcular aproximadamente o valor da integral directamente sen atopar antes a función primitiva.

Mediante cálculo de primitivas

A técnica máis básica para calcular integrais dunha variable real baséase noteorema fundamental do cálculo.Proceda do seguinte xeito:

1. Escolla unha funciónf(x) e un intervalo [a,b].
2. Procure unha primitiva def,é dicir, unha funciónFtal queF'=f.
3. Usando o teorema fundamental do cálculo, asumindo que nin o integrando nin a integral teñensingularidadesno camiño da integración,

   $\int _{a}^{b}f(x)\,dx=F(b)-F(a).$

4. Polo tanto, o valor da integral éF(b) −F(a).

O paso difícil neste proceso é moitas veces atopar unha primitiva def.Raramente é posible botarlle unha ollada a unha función e escribir a súa primitiva directamente. Moitas veces, é necesario utilizar unha das moitas técnicas que se desenvolveron para calcular integrais. A maioría destas técnicas transforman unha integral noutra que se espera que sexa máis sinxeliña. Estas técnicas inclúen:

• Integración por cambio de variábel
• Integración por partes
• Integración por redución
• Integración por substitución trigonométrica
• Integración de fraccións racionais

Aínda que estas técnicas fracasen, aínda é posíbel avaliar unha integral dada. Outras técnicas son:

• cálculo de residuos
• Integración por serie,usando por exemplo aserie de Taylordafcorrespondente.
• Identidade de Parseval
• Integral de Gauss.

O cálculo de volumes desólidos de revoluciónnormalmente pódese facer conintegración por discosouintegración por capas.

Os resultados específicos atopados usando as diferentes técnicas están listados nalista de integrais.

Algoritmos de cálculo simbólico

Artigo principal:Integración simbólica.

Moitos problemas de matemáticas, física e enxeñaría implican a integración onde se desexa unha fórmula explícita para a integral. Para este fin, ao longo dos anos publicáronse extensas listas de integrais. Coa expansión doscomputadores,moitos profesionais, educadores e estudantes recorreron aossistemas alxébricos computacionaisque foron deseñados especificamente para realizar tarefas tediosas ou difíciles, incluída a integración. A integración simbólica presenta un reto especial no desenvolvemento deste tipo de sistemas.

Na altura do 2024 algún destes sistemas son:Maxima,Maple,Mathematica,Sage.

Integración numérica

Artigo principal:Integración numérica.

Métodos de cadratura numérico: método do rectángulo, regra trapezoidal, método de Romberg, cadratura gaussiana

As integrais definidas pódense aproximar usando varios métodos deintegración numérica.

Ométodo do rectánguloconsiste en dividir a rexión baixo a función nunha serie de rectángulos correspondentes aos valores da función e multiplícase polo ancho do paso para atopar a suma.

Un enfoque mellor, aregra trapezoidal,substitúe os rectángulos usados ​​nunha suma de Riemann por trapecios. A regra trapezoidal pondera os valores primeiro e último pola metade, despois multiplica polo ancho do paso para obter unha mellor aproximación.

A idea que está detrás da regra trapezoidal, que as aproximacións máis precisas da función producen mellores aproximacións da integral, pódese levar máis aló: aregra de Simpsonaproxima o integrando mediante unha función cadrática por tramos.

As sumas de Riemann, a regra trapezoidal e a regra de Simpson son exemplos dunha familia de regras de cadratura chamadasfórmulas de Newton–Cotes.A regra de cadratura de graonNewton–Cotes aproxima o polinomio en cada subintervalo cun polinomio de graosn.Escóllese este polinomio para interpolar os valores da función no intervalo.As aproximacións de Newton–Cotes de grao superior poden ser máis precisas, mais requiren máis avaliacións de funcións e poden sufrir imprecisións numéricas debido aofenómeno de Runge.Unha solución a este problema é acadratura de Clenshaw–Curtis,na que se aproxima o integrando expandíndoo en termos depolinomios de Chebyshev.

Ométodo de Rombergreduce á metade o ancho de pasos de forma incremental, dando aproximacións trapezoidais indicadas porT(h₀),T(h₁),e así seguido, ondeh_k+1é a metade deh_k.Para cada tamaño de paso novo, só hai que calcular a metade dos novos valores da función; o resto tómanse do tamaño anterior. Despoisinterpolaun polinomio a través das aproximacións, e extrapola aT(0).

Acadratura gaussianaavalía a función nas raíces dun conxunto depolinomios ortogonais.O método gaussiano de {mvar|n} puntos é exacto para polinomios de grao ata2n− 1.

O cálculo de integrais de dimensións superiores (por exemplo, cálculos de volume) fai un uso importante de alternativas como aintegración de Monte Carlo.

Extensións

Integrais impropias

Artigo principal:Integral impropia.

Aintegral impropia$\int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi$ten intervalos ilimitados tanto para o dominio como para o intervalo.

Unha integral de Riemann "propia" asume que o integrando está definido e é finito nun intervalo pechado e limitado, entre corchetes polos límites da integración. Unha integral impropia ocorre cando unha ou máis destas condicións non se cumpren. Nalgúns casos, esas integrais pódense definir considerando olímitedunhasucesióndeintegrais de Riemannpropias en intervalos progresivamente maiores.

Se o intervalo está ilimitado, por exemplo no seu extremo superior, entón a integral impropia é o límite cando ese punto final vai cara a infinito:

$\int _{a}^{\infty }f(x)\,dx=\lim _{b\to \infty }\int _{a}^{b}f(x)\,dx.$

Se o integrando só está definido ou finito nun intervalo semiaberto, por exemplo(a,b],de novo un límite pode proporcionar un resultado finito:

$\int _{a}^{b}f(x)\,dx=\lim _{\varepsilon \to 0}\int _{a+\epsilon }^{b}f(x)\,dx.$

É dicir, a integral impropia é o límite das integrais propias xa que un punto final do intervalo de integración aproxímase a unnúmero realespecífico, ou∞,ou−∞.En casos máis complicados, esíxense límites en ambos os puntos finais ou nos puntos interiores.

Integración múltiple

Artigo principal:Integral múltiple.

A dobre integral calcula o volume baixo unha superficie$z=f(x,y)$

Do mesmo xeito que a integral definida dunha función positiva dunha variábel representa aáreada rexión entre a gráfica da función e o eixox,aintegral dobredunha función positiva de dúas variábeis representa ovolumeda rexión entre a superficie definida pola función e o plano que contén o seu dominio.Por exemplo, unha función en dúas dimensións depende de dúas variábeis reais,xey,e da integral dunha funciónfsobre o rectánguloRdado como oproduto cartesianode dous intervalos$R=[a,b]\times [c,d]$

$\int _{R}f(x,y)\,dA$

onde o diferencialdAindica que a integración se toma con respecto á área. Estaintegral dobrepódese definir usandosuma de Riemann,e representa o volume (con signo) baixo a gráfica dez=f(x,y)sobre o dominioR.En condicións axeitadas (por exemplo, sefé continua), oteorema de Fubiniindica que esta integral pode expresarse equivalentemente como dúas integrais consecutivas

$\int _{a}^{b}\left[\int _{c}^{d}f(x,y)\,dy\right]\,dx.$

Isto reduce o problema de calcular unha integral dobre a calcular dúas integrais unidimensionais consecutivas. Por iso, outra notación para a integral sobreRusa un signo de dobre integral:

$\iint _{R}f(x,y)\,dA.$

É posíbel a integración en dominios máis xerais. A integral dunha funciónf,con respecto ao volume, sobre unha rexiónDn-dimensional de$\mathbb {R} ^{n}$denótase mediante símbolos tal como:

$\int _{D}f(\mathbf {x} )d^{n}\mathbf {x} \ =\int _{D}f\,dV.$

Integrais de contorno

Artigo principal:Integración de contorno.

Naanálise complexa,o integrando é unhafunción con valores complexosdunha variábel complexazno canto dunha función real dunha variábel realx.Cando unha función complexa está integrada ao longo dunha curva$\gamma$no plano complexo, a integral denótase como segue

$\int _{\gamma }f(z)\,dz.$

Isto coñécese comointegral de contorno.

Un resultado fundamental na análise complexa é que a integral de contorno de1/zé2πi,onde o camiño do contorno considérase o círculo unitario percorrido en sentido antihorario (ou calqueracurva de Jordanorientada positivamente ao redor de 0). No caso do círculo unitario existe un método directo para avaliar a integral

$\oint _{C}{\frac {1}{z}}\,dz.$

Para avaliar esta integral, use o círculo unitario|z| = 1como contorno, parametrizado porz(t) =e^it,cont∈ [0, 2π],entóndz/dt=ie^it,por tanto,

$\oint _{C}{\frac {1}{z}}\,dz=\int _{0}^{2\pi }{\frac {1}{e^{it}}}ie^{it}\,dt=i\int _{0}^{2\pi }1\,dt=i\,t{\Big |}_{0}^{2\pi }=\left(2\pi -0\right)i=2\pi i$

que é o valor da integral. Este resultado só se aplica ao caso no que z se eleva á potencia de -1. Se a potencia non é igual a -1, entón o resultado sempre será cero.

Integrais de liña e integrais de superficie

Artigos principais:Integral de liñaeIntegral de superficie.

Unha integral de liña suma elementos ao longo dunha curva.

O concepto de integral pódese estender a dominios máis xerais de integración, como liñas curvas e superficies dentro de espazos de dimensións superiores. Esas integrais coñécense como integrais de liña e integrais de superficie respectivamente. Estas teñen importantes aplicacións en física, como cando se trata decampos vectoriais.

Unhaintegral de liña(ás veces chamadaintegral de camiño) é unha integral onde afunciónque se vai integrar avalíase ao longo dunhacurva.Están en uso varias integrais de liña diferentes.

A función a integrar pode ser uncampo escalarou uncampo vectorial.O valor da integral da liña é a suma dos valores do campo en todos os puntos da curva, ponderado por algunha función escalar na curva (normalmente alonxitude do arcoou, para un campo vectorial, oproduto escalardo campo vectorial cun vectordiferencialna curva).Esta ponderación distingue a integral de liña das integrais máis simples definidas enintervalos.Moitas fórmulas sinxelas en física teñen análogos continuos naturais en termos de integrais de liña; por exemplo, o feito de que otraballosexa igual aforza,F,multiplicado polo desprazamento,s,pódese expresar (en termos de cantidades vectoriais) como:

$W=\mathbf {F} \cdot \mathbf {s}.$

Para un obxecto que se move por un camiñoCnuncampo vectorialFcomo uncampo eléctricoou uncampo gravitacional,o traballo total realizado polo campo sobre o obxecto obtense sumando o traballo diferencial realizado ao pasar desas+ds.Isto dá a integral de liña

$W=\int _{C}\mathbf {F} \cdot d\mathbf {s}.$

A definición de integral de superficie basease en dividir a superficie en pequenos elementos de superficie.

Unhaintegral de superficiexeneraliza as integrais dobres á integración sobre unhasuperficie(que pode ser un conxunto curvo noespazo); pódese pensar como aintegral dobreanálogo daintegral de liña.A función a integrar pode ser uncampo escalarou uncampo vectorial.O valor da integral da superficie é a suma do campo en todos os puntos da superficie. Isto pódese conseguir dividindo a superficie en elementos de superficie, que proporcionan a partición para as sumas de Riemann.

Para un exemplo de aplicacións de integrais de superficie, considere un campo vectorialvnunha superficieS;é dicir, para cada puntoxenS,v(x)é un vector. Imaxine que un fluído flúe a través deS,de tal xeito quev(x)determina a velocidade do fluído enx.Ofluxodefínese como a cantidade de fluído que flúe porSnunha unidade de tempo. Para atopar o fluxo, hai que realizar oproduto escalardevcoanormal unitaria da superficieaSen cada punto, que dará un campo escalar, que será o que integemos sobre a superficie:

$\int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }.$

O fluxo de fluído neste exemplo pode ser dun fluído físico como auga ou ar, ou dun fluxo eléctrico ou magnético. Así as integrais de superficie teñen aplicacións en física, particularmente coa teoría clásica doelectromagnetismo.

Véxase tamén

Bibliografía

• Anton, Howard; Bivens, Irl C.; Davis, Stephen (2016).Calculus: Early Transcendentals(11th ed.). John Wiley & Sons.ISBN978-1-118-88382-2.
• Apostol, Tom M.(1967).Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra(2nd ed.). Wiley.ISBN978-0-471-00005-1.
• Bourbaki, Nicolas(2004).Integration I.Springer-Verlag.ISBN3-540-41129-1..In particular chapters III and IV.
• Burton, David M. (2011).The History of Mathematics: An Introduction(7th ed.). McGraw-Hill.ISBN978-0-07-338315-6.
• Cajori, Florian(1929).A History Of Mathematical Notations Volume II.Open Court Publishing.ISBN978-0-486-67766-8.
• Dahlquist, Germund;Björck, Åke (2008)."Chapter 5: Numerical Integration".Numerical Methods in Scientific Computing, Volume I.Philadelphia:SIAM.Arquivado dendeo orixinalo 2007-06-15.
• Feller, William(1966).An introduction to probability theory and its applications.John Wiley & Sons.
• Folland, Gerald B.(1999).Real Analysis: Modern Techniques and Their Applications(2nd ed.). John Wiley & Sons.ISBN0-471-31716-0.
• Fourier, Jean Baptiste Joseph(1822).Théorie analytique de la chaleur.Chez Firmin Didot, père et fils. p. §231.
• Gonzalez, Ivan; Jiu, Lin; Moll, Victor H. (1 January 2020).An extension of the method of brackets. Part 2.Open Mathematics(eninglés)18.pp. 983–995.ISSN2391-5455.arXiv:1707.08942.doi:10.1515/math-2020-0062.
• Heath, T. L.,ed. (2002).The Works of Archimedes.Dover.ISBN978-0-486-42084-4.
  (Originally published by Cambridge University Press, 1897, based on J. L. Heiberg's Greek version.)
• Hildebrandt, T. H.(1953).Integration in abstract spaces.Bulletin of the American Mathematical Society59.pp. 111–139.ISSN0273-0979.doi:10.1090/S0002-9904-1953-09694-X.
• Kahaner, David;Moler, Cleve;Nash, Stephen (1989). "Chapter 5: Numerical Quadrature".Numerical Methods and Software.Prentice Hall.ISBN978-0-13-627258-8.
• Kallio, Bruce Victor (1966).A History of the Definite Integral(PDF)(M.A. thesis). University of British Columbia. Arquivado dendeo orixinalo 2014-03-05.Consultado o2014-02-28.
• Katz, Victor J.(2009).A History of Mathematics: An Introduction.Addison-Wesley.ISBN978-0-321-38700-4.
• Kempf, Achim; Jackson, David M.; Morales, Alejandro H. (2015).How to (path-)integrate by differentiating.Journal of Physics: Conference Series626(IOP Publishing). p. 012015.Bibcode:2015JPhCS.626a2015K.arXiv:1507.04348.doi:10.1088/1742-6596/626/1/012015.
• Krantz, Steven G.(1991).Real Analysis and Foundations.CRC Press.ISBN0-8493-7156-2.
• Leibniz, Gottfried Wilhelm(1899). Gerhardt, Karl Immanuel, ed.Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern. Erster Band.Berlin: Mayer & Müller.
• Lieb, Elliott;Loss, Michael(2001).Analysis.Graduate Studies in Mathematics14(2nd ed.).American Mathematical Society.ISBN978-0821827833.
• Montesinos, Vicente; Zizler, Peter; Zizler, Václav (2015).An Introduction to Modern Analysis(illustrated ed.). Springer.ISBN978-3-319-12481-0.
• Rich, Albert; Scheibe, Patrick; Abbasi, Nasser (16 December 2018).Rule-based integration: An extensive system of symbolic integration rules.Journal of Open Source Software3.p. 1073.Bibcode:2018JOSS....3.1073R.doi:10.21105/joss.01073.
• Rudin, Walter(1987). "Chapter 1: Abstract Integration".Real and Complex Analysis(International ed.). McGraw-Hill.ISBN978-0-07-100276-9.
• Saks, Stanisław(1964).Theory of the integral(English translation by L. C. Young. With two additional notes by Stefan Banach. Second revised ed.). New York: Dover.
• Siegmund-Schultze, Reinhard(2008). "Henri Lebesgue". En Timothy Gowers; June Barrow-Green; Imre Leader.Princeton Companion to Mathematics.Princeton University Press.ISBN978-0-691-11880-2..
• Stillwell, John(1989).Mathematics and Its History.Springer.ISBN0-387-96981-0.
• Stoer, Josef;Bulirsch, Roland(2002). "Topics in Integration".Introduction to Numerical Analysis(3rd ed.). Springer.ISBN978-0-387-95452-3..
• Struik, Dirk Jan,ed. (1986).A Source Book in Mathematics, 1200-1800.Princeton, New Jersey: Princeton University Press.ISBN0-691-08404-1.
• Arabic mathematical notation.W3C.2006.

Outros artigos

• Lista de integrais
• Antiderivada ou Integral indefinida

Ligazóns externas

• "Integral".Encyclopedia of Mathematics.EMS Press.2001 [1994].
• Online Integral Calculator,Wolfram Alpha.
• Keisler, H. Jerome,Elementary Calculus: An Approach Using Infinitesimals,University of Wisconsin
• Stroyan, K. D.,A Brief Introduction to Infinitesimal Calculus,University of Iowa
• Mauch, Sean,Sean's Applied Math Book,CIT, an online textbook that includes a complete introduction to calculus
• Crowell, Benjamin,Calculus,Fullerton College, an online textbook
• Garrett, Paul,Notes on First-Year Calculus
• Hussain, Faraz,Understanding Calculus,an online textbook
• Johnson, William Woolsey (1909)Elementary Treatise on Integral Calculus,link fromHathiTrust.
• Kowalk, W. P.,Integration Theory,University of Oldenburg. A new concept to an old problem. Online textbook
• Sloughter, Dan,Difference Equations to Differential Equations,an introduction to calculus
• Numerical Methods of IntegrationatHolistic Numerical Methods Institute
• P. S. Wang,Evaluation of Definite Integrals by Symbolic Manipulation(1972) — a cookbook of definite integral techniques