Sudoku

Un sudoku antes de resolvelo...

... e coa súa resolución marcada en vermello.

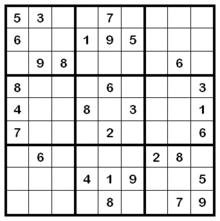
Sudoku(enxaponés:Sổ độc, sūdoku) é o nome dunquebracabezasmatemáticoque se inventou nosEstados Unidos,e que se fixo popular enXapónno1986,dándose a coñecer internacionalmente en2005.

O obxectivo do xogo é encher unha grella de 9×9 celas dividida en subgrellas de 3×3 coas cifras do 1 ao 9 partindo dalgúns números xa colocados nalgunhas das celas. Non se pode repetir ningunha cifra nunha mesma ringleira, columna ou rexión. Un sudoku está ben deseñado se a súa solución é única. A solución dun sudoku sempre é uncadrado latino,aínda que o recíproco en xeral non é certo, xa que o sudoku establece a restrición engadida de que non se pode repetir un mesmo número nunha rexión.

Numerososxornaiscomezaron a publicar sudokus desde o 2005 na súa sección depasatempos.

Historia

Este crebacabezas numérico pode terse orixinado enNova Yorkno ano1979.Naquel entón, a empresaDell Magazinspublicou este xogo, ideado porHoward Garns,baixo o nome deNumber Place( "o lugar dos números" ). É moi probable que o sudoku se crease a partir dos traballos deLeonhard Euler,famoso matemáticosuízodoséculo XVIII.O devandito matemático non creou o xogo en si, senón que utilizou o sistema chamado do cadrado latino para realizar cálculos de probabilidades.

Posteriormente, a editorialNikoliexportouno aoXapón,publicándoo no xornalMonthly Nikolist,en abril de1984,baixo o títuloSūji wa dokushin nen kagiru( sổ tự は độc thân に hạn る), que se pode traducir como "os números deben estar sós" ( độc thân significa literalmente "célibe, solteiro" ). FoiKaji Maki( hạ trị chân khởi ), presidente deNikoli,quen lle puxo o nome. Máis adiante o nome abreviouse aSūdoku( sổ độc;sū=número,doku= só); xa que é práctica común en xaponés tomar o primeirokanjide palabras compostas para abrevialas.

En1986,Nikoliintroduciu dúas innovacións que garantirían a popularidade do xogo: o número de cifras que viñan xa dadas estaría restrinxida a un máximo de 30 e sería "simétrico" (é dicir, as celas con cifras dadas estarían dispostas de formarotacionalmente simétrica). Isto non sempre se cumpre nos sudokus actuais. En1997,Wayne Gouldpreparou algúns sudokus para o diarioThe Times,que publicou bastante máis tarde, en decembro de2004.Tres días despois,The Daily Mailpublicou os seus sudokus co nomecodenumber.

No ano 2005, aICPC(International Collegiate Programming Contest) incluíu entre os seus 9 problemas o sudoku. Neste mesmo ano tamén ve a luz o primeiro libro sobre sudokus que publica un español,"Los mejores Sudokus"( "Os mellores sudokus" ), con 200 sudokus agrupados en 4 niveis de dificultade, cunha extensa descrición da historia deste pasatempo, así como das súas regras, e un exemplo paso a paso para a súa resolución. A este primeiro, seguíronlle 3 volumes máis, ademais dun libro sobrekakuros,outro sobrecadrados máxicos,e un máis sobre ocuboku.

Popularidade nos medios de comunicación

En1997,o xuíz xubilado deHong KongWayne Gould,de 59 anos de idade, unneozelandés,viu un destes crebacabezas parcialmente completado nunha libraría xaponesa. Durante uns 6 anos desenvolveu un programa de ordenador para poder producilo. Sabendo que osxornaisdoReino Unidoteñen unha longa tradición en canto á publicación deencrucilladose outros crebacabezas, promoveu o sudoku enThe Times,publicándoo o12 de novembrode2004e chamándooSu Doku.Os crebacabezas dePappocom,empresa desoftwarede Gould, imprimíronse diariamente noTimesdesde entón.

Tres días máis tarde,The Daily Mailcomezou a publicar o xogo baixo o nome decodenumber.The Daily Telegraphintroduciu o seu primeiro sudoku deMichael Mephamo19 de xaneirode2005e outros xornais doTelegraph Groupempezaron a darlle un oco nas súas páxinas.

Nationwide News Pty Ltd.comezou a publicar o crebacabezas enThe Daily TelegraphdeSydneyo20 de maiode2005;imprimíronse cinco crebacabezas con solucións ese día. A gran popularidade alcanzada polo sudoku nos xornais británicos fixo que internacionalmente o alcumaran nos medios de comunicación mundiais como o«crebacabezas co crecemento máis rápido no mundo».

Produce adicción

A escritoraCarol Vorderman,no seu libroCarol Vorderman's How To Do Sudokuexplica por que ela e moitas outras persoas gozan resolvendo sudokus.

Comenta as simples regras que ten o xogo, o que o fai sinxelo para os principiantes, xunto á carencia da necesidade de aritmética mental; a satisfacción de completar un crebacabezas, xa que son desafiantes e absorbentes; a rápida mellora das habilidades, cantos máis sudokus se resolvan, máis se melloran as habilidades; a súa facilidade para gardalo e continuar despois, unido á posibilidade de levar o anaco do xornal para resolvelo onde sexa.

Regras e terminoloxía

O sudoku preséntase normalmente como unha táboa de 9×9, composta por subgrellas de 3×3 denominadas "rexións" (tamén se lle chaman "caixas", ou "bloques" ). Algunhas celas xa conteñen números, coñecidos como "números dados" (ou ás veces "pistas" ). O obxectivo do xogo é cubrir as celas baleiras, cun número en cada unha delas, de tal forma que cada columna, fila e rexión conteña os números do 1 ao 9 sen que ningún apareza repetido. Ademais, cada número da solución aparece só unha vez en cada unha das tres "direccións", de aí o de que "os números deben estar sós", que evoca o nome do xogo.

Niveis de dificultade

A miúdo, os sudokus publicados clasifícanse segundo a súa dificultade. Aínda que resulta sorprendente, a cantidade de números dados apenas afecta á dificultade do sudoku, e mesmo pode non afectar en absoluto. Un sudoku cun mínimo de números dados pode ser moi fácil de resolver, e un con máis números pode ser complicado de resolver. Está baseado na relevancia e a posición dos números máis que na cantidade destes. Demostrouse que o problema de resolución de sudoku pertence a NP (problemas cuxa complexidade non é polinómica), polo tanto (en teoría) non se pode construír unalgoritmoque os resolva nun tempo polinómico.

Os programas informáticos que resolven sudokus poden estimar a dificultade que ten un humano para atopar a solución, baseándose na complexidade das técnicas de resolución necesarias. Esta estimación permite aos editores adaptar os seus sudokus para persoas con diferente experiencia resolutoria. Algunhas versiónsonlinetamén ofrecen varios niveis de dificultade.

Métodos para a resolución do sudoku

A rexión 3×3 da esquina superior esquerda debe conter un 7. Rastexando ao longo e ancho os setes localizados en calquera lugar da reixiña, o xogador pode eliminar todas as celas baleiras da esquina superior esquerda que non poden conter un 7. Isto deixa só unha cela posible (remarcada en verde).

A estratexia para resolver este crebacabezas pódese considerar como a combinación de tres procesos: escaneo, marcado e análise.

Escaneo

O escaneo realízase desde o principio e, durante toda a resolución. O escaneo pode ter que ser executado varias veces entre períodos de análise. O escaneo consta de dúas técnicas básicas: trama cruzada e reconto, que se poden usar alternativamente.

Trátase do escaneo de filas (ou columnas) para identificar que liña nunha rexión en particular pode conter un número determinado mediante un proceso de eliminación. Este proceso repítese entón coas columnas (ou filas). Para obter resultados máis rápidos, os números son escaneados de forma ordenada, segundo a súa frecuencia de aparición. É importante realizar este proceso, comprobando todos os díxitos do 1 ao 9.

• Reconto1-9 por rexións, filas e columnas para identificar números perdidos. O reconto baseado no último número descuberto pode aumentar a velocidade.

Marcado

Exemplo de onde iría cada número indicado polo método de marcado porpuntos.

O escaneo interrómpese cando non se poden descubrir novos números. Neste punto é necesario centrarse nalgunha análise lóxica. A maior parte da xente atopa útil guiar esta análise mediante o marcado de números candidatos nas celas baleiras. Hai dúas notacións populares: subíndices e puntos.

▪Na notación desubíndice,os números candidatos escríbense en pequeno nas celas nas que poden ir. A desvantaxe é que os puzzles orixinais se publican en xornais que habitualmente non deixan demasiado espazo para acomodar máis que uns poucos díxitos. Se se usa esta notación, os resolutores crean, a miúdo, unha copia máis grande do puzzle e empregan un lapis afiado.

▪A segunda notación é un patrón depuntos.Cun punto na esquina superior esquerda represéntase un 1, e cun punto na esquina inferior dereita representa un 9. Esta notación ten como vantaxe que se pode usar no puzle orixinal. Requírese destreza para o emprazamento dos puntos, porque a existencia de puntos desprazados ou marcas inadvertidas leva, inevitablemente, á confusión e non son sinxelos de borrar sen engadir máis confusión.

Análise

Hai dous aproximacións principais: eliminación e«e se...».

• Naeliminación,o progreso realízase mediante a sucesiva eliminación de números candidatos para unha ou máis celas, ata deixar só unha elección posible. Despois de lograr cada resposta, debe realizarse un novo escaneo (habitualmente comprobando o efecto do último número). Hai unha serie de tácticas de eliminación. Unha das máis comúns é o "borrado do candidato non cuadrante". As celas con idéntica configuración de números candidatos dise que cadran se a cantidade de números candidatos en cada unha é igual ao número de celas que os conteñen. Por exemplo, dise que celas cadran cunha particular fila, columna ou rexión se dúas celas conteñen o mesmo par de números candidatos (p, q) e non outros, ou se tres celas conteñen o mesmo triplete de números candidatos (p, q, r) e non outros. Estas son, esencialmente, continxencias cuadrantes. Estes números (p, q, r) que aparecen como candidatos en calquera lugar na mesma fila, columna ou rexión en celas non cuadrantes, poden ser borrados.
• Na aproximación«e se...»,selecciónase unha cela con só dous números candidatos e realizase unha conxectura. As etapas de enriba repítense a menos que se atope unha duplicación, en cuxo caso o candidato alternativo é a solución. En termos lóxicos este método coñécese comoredución ao absurdo.Nishioé unha forma limitada desta aproximación: para cada candidato para unha cela, a cuestión é: entrará un número particular dunha configuración noutro emprazamento? Se a resposta é si, entón ese candidato pode ser eliminado. A aproximación«e se...»require un lapis e unha goma. Esta aproximación pode ser desaprobada por puristas lóxicos por demasiadoensaio e erropero pode chegar a solucións clara e rapidamente.

Idealmente necesítase atopar unha combinación de técnicas que eviten algún dos inconvenientes dos elementos de enriba. O reconto de rexións, filas e columnas pode resultar aburrido. Escribir números candidatos en celas baleiras pode consumir demasiado tempo. A aproximación«e se...»pode ser confusa a menos que sexas ben organizado. Oquidda cuestión é atopar unha técnica que minimice o reconto, o marcado e o borrado.

Resolución do sudoku por ordenador

Para osprogramadoresé relativamente sinxelo construír unha procura polo método debacktrackingou "volta atrás". Esta asignaría un valor (supoñamos que 1, ou o máis próximo a 1 dispoñible) á primeira cela dispoñible (supoñamos que a superior esquerda) e entón continuar asignando o seguinte valor dispoñible (supoñamos que 2) á seguinte cela dispoñible. Isto continuaría así ata que se descubrise unha duplicación, en cuxo caso, o seguinte valor alternativo se colocaría no primeiro campo alterado. No caso de que ningún valor cumprise a restrición retrocederíase ata o cadro anterior e probaríanse os seguintes números.

Aínda que lonxe daeficiencia computacional,este método atopará a solución se se permite o suficiente tempo de computación. Un programa máis eficiente podería deixar unha pegada de valores potenciais para as celas, eliminando valores imposibles ata que só un valor quedase para unha cela determinada. Entón cubriríase esa cela e usaríase esa información para máis eliminacións e así sucesivamente ata o final. Isto emularía máis exactamente o que un resolutor humano faría sen o método deensaio e erro.

Codificar a procura para imposibilidades baseadas en continxencias e mesmo múltiples continxencias (como sería requirido para os sudoku máis difíciles) é abondo complexo de construír a man. De calquera modo, tales complicacións son innecesarias se todo o que o programador desexa facer é atopar unha solución eficientemente. Unha forma máis eficiente de construír solucións involucra ferramentas de programación máis avanzadas.

Algúns programas así construídos, que emulan a resolución humana, permiten estimar a dificultade que terá un humano para atopar a solución.

Construción

É posible estabelecer sudokus con máis dunha solución e tamén realizar taboleiros iniciais de sudoku sen solución, pero non se consideran sudoku apropiados; como a maior parte dos crebacabezas lóxicos, espérase unha solución única.

A construción dun crebacabezas sudoku pode ser realizada a man eficientemente predeterminando as posicións dos números dados e asignándolles valores para realizar un proceso dedutivo. Pénsase que os sudokusNumber PlacedeDellestán xerados porordenador.Normalmente teñen máis de 30 números dados espallados aparentemente de forma aleatoria, algúns dos cales poden ser deducidos a partir doutros números dados. Tamén teñen créditos sen autoría (é dicir, o nome do construtor non se imprime xunto a ningún puzzle).Wei-Hwa Huangasegura que Dell lle encargou escribir un programa xeradorNumber Placeeninvernodo ano2000;antes diso, lle dixeron que os sudokus eran realizados a man. O xerador foi escrito conVisual C++,e aínda que tiña opcións para xerar máis crebacabezas de estilo xaponés, con restricións simétricas e menos números, Dell optou por non usar esas funcións, polo menos non ata a súa recente publicación das revistas compostas por sudokus.

Os sudokuNikoliconstrúense a man, e o nome do autor aparece nos créditos xunto a cada rompecabezas; os números dados sempre se atopan en forma dun patrón simétrico. Os quebracabezasNumber Place Challengerde Dell (véxaseVariantesmáis abaixo) tamén citan os créditos do autor. Os sudoku que aparecen na maioría dos xornais doReino Unidoaparentemente son xerados por ordenador, pero empregan números dados simétricos.The Guardianlicenza e publica sudoku construídos conNikoli,aínda que non inclúe créditos de autoría.The Guardiandeclarou que xa que eran realizados a man, os seus quebracabezas conterían "ocorrencias imperceptibles" que serían pouco probables en sudokus xerados por ordenador. O desafío para os programadores de sudokus é aprender a un programa como construír crebacabezasintelixentes,de forma que non se poidan distinguir daqueles realizados por humanos;Wayne Gouldnecesitou retocar o seu popular programa durante seis anos para crer que alcanzase ese nivel.

Variantes

Exemplo dun sudoku nonomino.

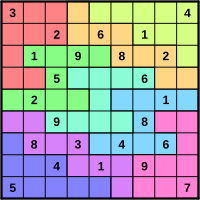
Aínda que os sudokus de 9×9 con rexións de 3×3 son, por moito, os máis comúns, e abundan numerosas variantes. Por exemplo, hai sudokus de táboas de 4×4 con rexións de 2×2; estes publicáronse baixo o nome deLogi-5táboas de 5×5 con rexiónspentaminó;oWorld Puzzle Championshiprealizou previamente unha táboa de 6×6 con rexións de 2×3 e unha táboa de 7×7 con seis rexiónsheptominoe unha rexión disxunta;Daily SuDokuofrece sudokus de 4×4, 6×6 e 9×9 sinxelos cada día baixo o nome deDaily SuDoku for Kids.Mesmo o sudoku de 9×9 non é sempre estándar, eEbbpublica regularmente algúns deles con rexiónsnonomino;osOU.S. Puzzle Championshipde2005tiñan un sudoku con rexións deparalelogramosdispostas ao redor do bordo externo do crebacabezas, como se a táboa fosetoroidal.Tamén se poden realizar sudokus máis grandes, como oMonster SuDokude 12×12 deDaily SuDoku,osNumber Place Challengerde 16×16 que publica Dell regularmente e o desafianteSudoku o XigantebehemothsdeNikolide 25×25.

Outra variante común consiste en estabelecer restricións adicionais para forzar a posición dos números máis aló dos habituais requirimentos encanto á fila, columna e rexión. A miúdo, as restricións toman a forma dunha "dimensión" extra; a máis común é que se cumpra o requirimento de que os números das diagonais principais tamén sexan únicos. Os mencionados sudokusNumber Place Challengerforman parte desta variante, así como o son osSudoku XdoDaily Mail,que utiliza reixiñas de 6×6. ODaily Mailtamén publica oSuper Sudoku Xna súa revistaWeekend:un reixiña de 8×8 na que as filas, columnas, diagonais principais, bloques de 2×4 e bloques de 4×2 conteñen cada número unha soa vez. Outra variante consiste en empregar díxitos coa mesma posición relativa dentro das súas respectivas rexións; ditos quebracabezas se imprimen a miúdo a toda cor, de forma que cada grupo disxunto comparte unha cor para maior claridade.

Outras clases de restricións extra poden ser matemáticas, como requirir que os números en segmentos delineados da rexiña teñan sumas específicas ou produtos (un exemplo anterior sería oKiller Su DokuenThe Times). Tamén son frecuentes os crebacabezas construídos a partir de múltiples sudokus. As rexiñas de 9×9 que se superpoñen nas rexións das esquiñas en forma dunquincuncioson coñecidas noXapóncomo sudokuGattai 5(mestura de cinco), pero tamén reciben o nome deSuper Sudoku.EnThe TimeseThe Sydney Morning Heralda este tipo de sudokus lles chamanSamurai SuDoku(Sudoku Samuráienespañol). Sudokus con 20 ou máis rexións que se superpoñen son comúns nalgunhas publicacións xaponesas. A miúdo, non se ofrecen números dados nas rexións solapadas. Tamén se publican reixas secuenciais, en contraposición ás solapadas, con valores en lugares específicos nas reixas que necesitan ser trasferidas a outras.

Tamén emerxeron variacións alfabéticas, que utilizan letras en lugar de números. Por suposto, non hai diferenza funcional no quebracabezas, salvo que as letras soletren algo, formando unha palabra. As variantes recentes inciden nisto, a miúdo facendo que apareza unha palabra nunha das diagonais principais unha vez solucionado o sudoku; a determinación da palabra pódese ver como unha axuda por adiantado para chegar á solución. OCode DokuArquivado12 de setembro de 2007 enWayback Machine.ideado por Steve Schaefer ten unha oración enteira encaixada no crebacabezas; o Super WordokudeTop Notchrepresenta dúas palabras de 9 letras, unha en cada diagonal. É discutible se estes son verdadeiros sudokus: aínda que presumiblemente teñen unha soa solución valida, non teñen porque ter que ser solucionados baseándose na lóxica, necesitando que o que o resolva determine cales son as palabras incrustadas.Top Notchalega que esta é unha característica que se deseñou para derrotar aos programas de resolución de sudokus.

A continuación móstranse algunhas das variacións únicas máis importantes:

• Un sudoku tridimensional foi inventado porDion Churche publicado noDaily Telegraphenmaio de 2005.
• OU.S. Puzzle Championshipde2005inclúe unha variante denominadaDixital Number Place:en lugar de números dados, a maioría das celas conteñen un número parcial —un segmento dun número, cos números escritos como se formasen parte dundisplayde sete segmentos.
• Wei-Hwa Huangcreou un meta-sudoku,onde o obxectivo é acabar debuxando os bordos dunha rexión pentomino dunha reixiña de 5×5 para deixar un quebracabezas único resoluble con rexións sen unha forma idéntica.
• Cuboku,un invento deAgustín Fonsecapartindo da frase:«o sudoku é aos pasatempos o que uncubo de Rubikaos crebacabezas».

Véxase tamén

Outros artigos

• Cuboku.

Ligazóns externas

• SudokuenCurlie(eninglés)