עקרון הויגנס

שבירת גלים על פי עקרון הויגנס

עקרון הויגנס(ידוע גם כעקרון הויגנס-פרנל) קובע כי ניתן להתייחס לכל נקודה בחזית גלכמקור נקודתי שלגלחדש: כל נקודה שמופרעת על ידי מעבר של גל דרכה הופכת למקור שלגל כדורי,וההתאבכותשל כל הגלים הכדוריים היא הגל הכולל המתקדם במרחב. העיקרון נוסח על ידיכריסטיאן הויגנסואוגוסטן ז'אן פרנל.על עיקרון זה מבוסס הניתוח המתמטי של תופעת העקיפהכמו בניסוי שני הסדקיםשלתומאס יאנג.באמצעות עיקרון זה ניתן גם להסביר תופעות התאבכות נוספות ושבירה.

היסטוריה

ב-1678, הויגנס הציע כי כל נקודה אליה מגיעה הפרעה אורית הופכת למקור של גלים כדוריים; הסיכום של כל הגלים המשניים האלו קובע את צורת הגל בכל רגע נתון. הוא הניח שהגלים המשניים נעים פחות או יותר רק בכיוון "חזיתי", אולם לא הסביר לפי התאוריה שלו מדוע זה כך. הוא היה מסוגל לתת הסבר איכותי להתקדמות גלים קווית וכדורית, ולגזור את חוקיההחזרהוהשבירהבאמצעות העיקרון הזה, אבל לא יכול היה להסביר את הסטיות מתנועה ישרה המתרחשות כאשר אור פוגש בפינות, מפתחים ומסכים, אפקטים שזכו לשם "תופעותעקיפה".את הסיבה לשגיאה הזאת שלו הסביר דייוויד מילר ב-1991; הפתרון הוא שמקור הגלים הוא דיפול (ולא המונופול שהויגנס הניח), אשר מתקזז בכיוון המוחזר^{[דרושה הבהרה]}.

ב-1818, פרנל הראה שעקרון הויגנס יחד עם עקרון ההתאבכותשלו יכולים להסביר הן את ההתקדמות הקווית של אור והן את תופעות העקיפה. כדי להשיג התאמה עם תוצאות ניסוייות, הוא היה חייב לכלול בתאוריה שלו הנחות שרירותיות נוספות על הפאזה והמשרעת של הגלים המשניים, כמו גם גורם הטיה (obliquity factor). להנחות הללו לא היה בסיס פיזיקלימוצקאולם הן הובילו לתחזיות שהסכימו עם תצפיות ניסוייות כמו כתם אראגו (Arago spot).

כתם אראגו התגלה בעקבות רעיונו שלפואסוןשהיה חבר באקדמיה הצרפתית, אשר בחנה את עבודתו של פרנל. הוא נעזר בתאוריה של פרנל כדי להסיק שאמור להופיע כתם בהיר במרכז הצל של דיסקה קטנה, והסיק מכך שזה לא נצפה שהתאוריה הייתה שגויה. מאוחר יותר, אראגו, חבר אחר בוועד השופטים, ערך את הניסוי והראה שהתחזית נכונה. זו הייתה אחת החקירות שהובילו לניצחון התאוריה הגלית על פני התאוריה החלקיקית של האור, שהייתה דומיננטית במאה שעברה.

נוסחת העקיפה של קירכהוףסיפקה מסגרת מתמטיתריגורוזילעקיפה, המתבססת עלמשוואת הגלים.ההנחות השרירותיות אותן עשה פרנל כדי להגיע לניסוח המתמטי של עקרון הויגנס צצות באופן טבעי מהמתמטיקה של תורת העקיפה של קירכהוף.

הניסוח המתמטי של העיקרון

המחשה גאומטרית לחישוב של פרנל.

נתייחס למקרה של מקור נקודתי הממוקם בנקודהP₀,המייצר גלים בתדירותf.את ההפרעה ניתן לתאר על ידי המשתנה המרוכבU₀,הנקרא גםמשרעת מרוכבת.הוא מפיק גלים כדוריים עםאורך גלλ ומספר גלk=2π/λ.המשרעת המרוכבת של הגל הראשי בנקודהQהממוקמת במרחקr₀מהנקודהP₀ניתנת בביטוי:

$U(r_{0})={\frac {U_{0}e^{ikr_{0}}}{r_{0}}}$

מכיוון שהמשרעתקטנה ביחס הפוך למרחק ממקור הגל, והפאזה משתנה לפי מכפלת מספר הגלkבמרחק מהמקור.

באמצעות התאוריה של הויגנס ועקרון הסופרפוזיציהשל גלים, המשרעת המרוכבת בנקודה מרוחקת יותרPנמדדת על פי סיכום התרומות מכל נקודה על פני הכדור ברדיוסr₀.כדי להשיג התאמה עם תצפיות ניסוייות, פרנל מצא שהתרומות מהגלים המשניים שנוצרים מנקודות על פני הכדור חייבים להיות מוכפלים בקבוע$-i/\lambda$(כאשר$i={\sqrt {-1}}$), ובפקטור הטיה נוסף$K(\chi )$.ההתאמה הראשונה פירושה שהגלים המשניים מאחרים ביחס לגל הראשי ברבע מחזור גל, ושהמשרעת של הגלים המשניים היא ביחס של$1:\lambda$עם משרעת הגל הראשי. הוא הניח גם של-$K(\chi )$יש ערך מרבי כאשר$\chi =0$(כלומר: בכיוון התקדמות הגל הראשי), וערך מאופס כאשר$\chi =\pi /2$(כלומר: בניצב לכיוון התקדמות הגל הראשי).

על כן, המשרעת המרוכבת ב-Pנתונה בנוסחה:

$U(P)=-{\frac {i}{\lambda }}U(r_{0})\int _{S}{\frac {e^{iks}}{s}}K(\chi )\,dS$

כאשרSהוא המשטח של הכדור, ו-sהוא הרדיוס-וקטורביןQל-P.

ההנחות השונות שעשה פרנל מתקבלות באופן אוטומטי בנוסחת העקיפה של קירכהוף,אשר ניתן לראות את עקרון הויגנס-פרנל כקירוב לה. עם זאת, התוצאה של קירכהוף נבדלת מזו של פרנל בפקטור ההטיה$K(\chi )$:

$~K(\chi )={\frac {1}{2}}(1+\cos \chi )$

ל-Kיש מקסימום ב-$\chi =0$כמו בעקרון הויגנס-פרנל; אף על פי כן,Kלא שווה לאפס כאשר$\chi =\pi /2$.נוסחת קירכהוף מסבירה מדוע בכלל גלים מתקדמים בכיוון מוגדר מסוים: כאשר$\chi =\pi$,מקבלים 0 =$K(\chi )$,כלומר הגלים המשניים כלל לא מועברים לאחור.

עקיפה

עקיפה בסדק יחיד

בניסויי עקיפה,גל מישוריפוגע במחסום בעלמיפתחבצורה כלשהי (סדק יחיד, סדק כפול, שריג וכדומה), ומודדים את תבנית ההתאבכותשל הגל על מסך שנמצא בעברו השני של המחסום. לפי עקרון הויגנס, התבנית המתקבלת זהה לזו שמתקבלת מאוסף אינסופי של מקורותנקודתייםהממלאים את המפתח. כתוצאה מכך מגיע הגל, מעבר למחסום, גם לאזורים שבהם הוא כביכול לא יכול להגיע על פיאופטיקה גאומטרית,העוסקת בתנועת אור בקווים ישרים בלבד.

תיאור מתמטי

המשוואה שמקיים גל ממקור נקודתי היאמשוואת הלמהולץהלא-הומוגנית:

$\nabla ^{2}U+k^{2}U({\vec {r}},{\vec {r'}})=\delta ({\vec {r}}-{\vec {r'}})$

כאשר$\delta ({\vec {r}}-{\vec {r'}})$היאפונקציית דלתא של דיראקהתלת-ממדית, המתאפסת בכל המרחבפרט לנקודה${\vec {r}}={\vec {r'}}$.הגל המונוכרומטיהתלוי בזמן שפותר אתמשוואת הגליםמתקבל על ידי הכפלת$U({\vec {r}},{\vec {r'}})$בפונקציה$\ e^{-i\omega t}$. מאחר שפונקציית דלתא תלויה רק במרחק מהראשית ולא בזווית המרחבית, כי אז לאחר החלפת המשתנים:${\vec {R}}={\vec {r}}-{\vec {r'}}$ניתן להשתמש רק בחלק הרדיאלי שלאופרטורהלפלסיאןבקואורדינטות כדוריות:

$\nabla ^{2}U={\frac {1}{R}}{\frac {\partial ^{2}}{\partial R^{2}}}(RU)$

כאשר$R=|{\vec {R}}|$.

המשוואה הופכת להיות:

${\frac {\partial ^{2}}{\partial R^{2}}}(RU)+k^{2}RU=R\delta ({\vec {R}})$

מאחר שהפונקציה R מתאפסת בנקודה היחידה שבה פונקציית דלתא איננה מתאפסת, אגף ימין של המשוואה מתאפס באופן זהותי. פתרון המשוואה בקואורדינטות המקוריות הוא:

$U({\vec {r}},{\vec {r'}})\propto {\frac {1}{|{\vec {r}}-{\vec {r'}}|}}e^{ik|{\vec {r}}-{\vec {r'}}|}$

זוהימשוואההמתארתגל כדורי,הבוקע מהנקודה${\vec {r'}}$.את קבוע הפרופורציהניתן למצוא באמצעותתנאי שפה.בנוסף, הפונקציה שהתקבלה היא לפי ההגדרהפונקציית גריןשל המשוואה. לפימשפט גרין,משוואת הגל שנוצר ממקור דו-ממדי שאינו נקודתי ניתנת לחישוב באמצעות פונקציה זו על ידי האינטגרל המשטחי:

$U({\vec {r}})={\frac {k}{2\pi i}}\int \!\!\!\int U_{0}({\vec {r'}}){\frac {e^{ik|{\vec {r}}-{\vec {r'}}|}}{|{\vec {r}}-{\vec {r'}}|}}\cos \theta d^{2}r'$

כאשר$\ U_{0}$הוא מקור הגל,$\theta$היא הזווית בין וקטור השטח האינפיניטסימלי לבין הווקטור${\vec {r}}-{\vec {r'}}$,והאינטגרל הוא על המשטח המחולל את הגל. אינטגרל זה מבטא את הגל הנצפה כסופרפוזיציה של גלים כדוריים, הבוקעים מנקודות שונות על פני המשטח.

בפרט, אם במישור z=0 ניצב מחסום שלאחריו מתקבל הגל:$\ U(x,y,z=0)$,אז על מסך במרחק z מתקבלת תבנית העקיפה:

$U(x,y,z)={\frac {k}{2\pi i}}\int \!\!\!\int U(x',y',z=0){\frac {e^{ik|{\vec {r}}-{\vec {r'}}|}}{|{\vec {r}}-{\vec {r'}}|}}\cos \theta dx'dy'$

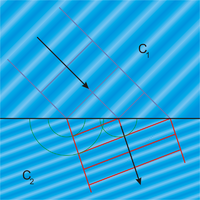
שבירה

כאשר גל מישורי פוגע בגוף העשוי משני חומרים שונים, המוצמדים במישור, הגל מעורר על המישור אוסף של גלים כדוריים ממקורות נקודתיים, שממלאים את כל מישור ההפרדה.מהירות האורבחומר דיאלקטריתלויה במקדם השבירהשלו. לכן, אם שני החומרים הם בעלי מקדמי שבירה שונים, אז חצי הכדור המתפשט לעבר החומר האחד יתקדם במהירות שונה מאשר חצי הכדור המתפשט לעבר החומר האחר. במקרה הכללי, שבו הגל מגיע למישור המפריד בזווית כלשהי שאינה אפס (כלומר, לא בניצב למישור), תיווצרזווית(שאינה אפס) בין הכיוון המאונך לחזית הגל הפוגע לבין זה של הגל הנשבר. תופעה זו מודגמת, למשל, במקרה של שבירה של אור במעבר הגבול בין שני חומרים. את זווית השבירה ניתן לחשב משיקולים גאומטריים, ולקבל אתחוק סנל.

לקריאה נוספת

• Joseph W. Goodman,Introduction to Fourier Optics,2nd edition, McGraw-Hill, 1996, Chapter 3

• ריצ'רד פיינמן(1988),אור וחומר,הוצאת הקיבוץ המאוחד

קישורים חיצוניים

• עקרון הויגנס,באתראנציקלופדיה בריטניקה(באנגלית)