Kubični kristalni sustav
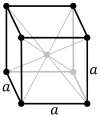
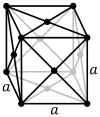
Kristalna rešetka kubičnog sustava okarakterizirana je s tri vektora elementarne translacije pakristalografski osni križima tri osi (x,y,z) iste duljine koje su međusobno pod pravim kutom.[1]
a = b = c, α = β = γ = 90°

|
|
|
Kristalna rešetka je s tri osi četvrtog stupnja i moguće su triBravaisove rešetke:osnovna, unutarnje centrirana i površinski centrirana.
Ako se na kristalu javlja potpuni broj elemenata simetrije koji je karakterističan za ovu vrstu kristalne rešetke tada kristal ima holoedrijski oblik. Ako postoji redukcija u broju nekih elemenata riječ je o parahemiedriji a ako nedostaje centar simetrije riječ je o antihemiedriji.

Osnovni oblici u kubičnoj holoedriji jesu:
- Kocka ili heksaedar {001},
- Rombododekaedar {011},
- Ikositetraedar {hhl},
- Heksaoktaedar {hkl},
- Oktaedar {111},
- Tetraheksaedar {0kl},
- Trioktaedar {hll}.
Ove se jednostavne forme u procesukristalizacijemogu međusobno preslagivati i graditi različite kristalne kombinacije.
Osim holoedrije u kubičnom se sustavu javljaju i kristali u parahemiedriji i antihemiedriji.
Osnovni oblici kubične parahemiedrije jesu:
- pentagondodekaedar {210} i
- diakizdodekaedar {132}.
I u kubičnoj parahemiedriji tijekom kristalizacije moguć je nastanak kristalnih kombinacija.
KristalipiritaFeS2iKatijeritaCoS2mogu biti oblika pentagondodekaedra a pirit može imati kristale oblika diakizdodekaedra.
Osnovni oblici kubične antihemiedrije jesu:
- tetraedar {111},
- trigondodekaedar {211},
- deltoiddodekaedar {221},
- hemiheksaoktaedar {132}.
- ↑Kemijski rječnik,,pristupljeno 14. svibnja 2013.

