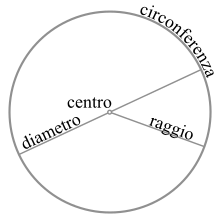
Cerchio

Ingeometria pianailcerchioè la parte di piano delimitata da unacirconferenzaed è costituito dall'insieme infinito deipuntiche distano da un punto dato, dettocentro,non più di una distanza fissata dettaraggio. In unsistema di assiun generico cerchio di centro$(a;b)$e raggio$r$è rappresentato dall'insieme di punti che soddisfano la seguente condizione:

${\overline {D}}=\{(x,y)\in {\mathbb {R} ^{2}}:(x-a)^{2}+(y-b)^{2}\leq r^{2}\}.$

Esso può essere immaginato come unpoligono regolarecon un numero di lati infinito, o meglio come il limite di una successione di poligoni regolari ad$n$lati per$n$che tende ad infinito. Il cerchio è una figura convessa.

Unsegmentoavente gli estremi sulla circonferenza è dettocorda;ognuna delle due parti in cui questa divide il cerchio si chiamasegmento circolare.Se la corda in questione passa per il centro, essa si chiamadiametroe i due segmenti sono congruenti e si chiamanosemicerchi.

Un segmento circolare può anche essere la parte di cerchio compresa tra due corde parallele.

L'intersezione fra unangoloal centro, cioè un angolo avente come vertice il centro del cerchio, ed il cerchio stesso (visivamente, uno "spicchio" di cerchio) si chiamasettore circolare.Se l'angolo al centro è retto, il settore circolare che individua si chiamaquadrante;se è piatto, è il semicerchio.

Due cerchi aventi lo stesso centro si diconoconcentrici.L'area compresa fra le due circonferenze si chiamacorona circolare.

La formula dell'area del cerchio può essere ottenuta come limite di quella del poligono regolare, ovvero come lunghezza della circonferenza per raggio diviso$2$:

$\mathrm {Area} ={\frac {\mathrm {circonferenza} \times \mathrm {raggio} }{2}}=\pi r^{2}.$

Laquadratura del cerchiosi riferisce all'impossibile compito di costruire con riga e compasso, a partire da un cerchio, unquadratoavente stessa area.

Alcuni solidi tridimensionali che possono avere, se tagliati da un piano, sezioni circolari sono lasfera,ilcilindroed ilcono.

Il cerchio viene dettoinscrittoin un poligono quando la sua circonferenza ètangentead ogni lato di quest'ultimo, ecircoscrittoquando i vertici di un poligono stanno sulla circonferenza.

L'area

Metodo euristico archimedeo

Metodo di Archimede per ridurre l'area del cerchio ad un triangolo equivalente

Come sappiamo da una lettera di Archimede adEratostene,Archimede non disdegnava metodi empirici per arrivare ai suoi risultati che poi dimostrava rigorosamente per altre vie. Il matematico immaginò di suddividere il cerchio in tante circonferenze concentriche e di svolgerle poi in segmenti fino a formare un triangolo mostrando così che ogni cerchio è equivalente a un triangolo che ha per base la circonferenza e per altezza il raggio:$(2\pi r)r{\frac {1}{2}}=\pi r^{2}$.

Integrazione con lecoordinate polari

Il valore dell'area del cerchio può venir visto come il valore dell'integrale doppio della funzione$f(x,y)=1$su un insieme coincidente con il cerchio. In formule si ha$\iint _{cerchio}1dxdy.$.Utilizzando il cambio di coordinate dacartesianea polari si ottiene$\int _{0}^{2\pi }\int _{0}^{R}\rho d\rho d\theta$,dove$\rho$e$\theta$sono le variabili polari. Al posto della funzione integranda$f(x,y)=1$abbiamo$f(\rho,\theta )=\rho$per via delcambio base.A questo punto l'integrale doppio si può scomporre nel prodotto di due integrali, in quanto le variabili sono separabili. Si ottiene

$\int _{0}^{2\pi }d\theta \cdot \int _{0}^{R}\rho d\rho =2\pi \cdot {\frac {1}{2}}R^{2}=\pi R^{2}.$

Integrazione "a cipolla"

Un metodo di integrazione per calcolare l'area del cerchio

Un primo approccio, tramite gliintegrali,al calcolo dell'area del cerchio può essere fatto pensando che questa superficie è data dalla somma progressiva di infiniti cerchi concentrici che hanno come valore massimo lacirconferenzae come minimo il centro del cerchio. In pratica è come se sommassimo tra di loro infiniti anelli, aventi ognuno spessore infinitesimo. Da questa rappresentazione comprendiamo come il nomea cipolladerivi proprio dalla stratificazione del cerchio, come quella di unacipolla,anche se in due dimensioni. Possiamo dunque chiamare$t$ilraggiodel cerchio a cui corrisponde ogni singola circonferenza, la cuilunghezzaè$2\pi t$(notiamo che in questa dimostrazione si dà per assunto questo dato). Quindi possiamo integrare (integrazione definita)$2\pi t\,dt$,cioè la funzione che ci dà le diverse circonferenze (separate dal fattoreinfinitesimo$dt$), tra il valore minimo e massimo dei loro raggi,$0$e$r$.

$\mathrm {Area} (r)=\int _{0}^{r}2\pi t\,dt=\left[(2\pi ){\frac {t^{2}}{2}}\right]_{t=0}^{r}=\pi r^{2}.$

Integrazione della semicirconferenza nel piano cartesiano

Per procedere al calcolo dell'areadi un cerchio attraverso un secondo metodo consideriamo innanzitutto unacirconferenzaconcentronell'origine degliassi;questo ci permette infatti di semplificare il caso generico di una circonferenzatraslatarispetto all'origine, dato che la traslazione non modifica l'area.

L'equazione di una circonferenza di generico raggio$r$e centro nell'origine degli assi è:

$x^{2}+y^{2}=r^{2}.$

Come sappiamo dalla definizione la suddetta formula non è unafunzione,in quanto associa ad alcuni punti più di unpunto.Per risolvere questo inconveniente eintegrarela funzione è sufficiente, dopo averla esplicitata rispetto alleordinate,$y=\pm {\sqrt {r^{2}-x^{2}}}$,prenderne solo leimmagininon negative.

Avremo quindi che l'equazionedella funzione che ci descrive la semicirconferenza con centro nell'origine di generico raggio$r$è

$y={\sqrt {r^{2}-x^{2}}}.$

Per conoscere quindi l'area del cerchio completo basta calcolare l'area sottesa alla funzione, tra$-r$e$r$:

$\int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,dx.$

Svolgiamo quindi i calcoli, ricorrendo alteorema fondamentale del calcolo integrale:

$\int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,dx$	$=\left[\int {\sqrt {r^{2}-x^{2}}}\right]_{-r}^{r}=$
	$=\left[{\frac {1}{2}}\left(r^{2}\arcsin \left({\frac {x}{r}}\right)+x{\sqrt {r^{2}-x^{2}}}\right)\right]_{-r}^{r}=$
	$={\frac {1}{2}}{{r^{2}}\arcsin \left({\frac {r}{r}}\right)}+{\frac {1}{2}}{r{\sqrt {r^{2}-r^{2}}}}-{\frac {1}{2}}{{r^{2}}\arcsin \left({\frac {-r}{r}}\right)}-{\frac {1}{2}}(-r){\sqrt {r^{2}-r^{2}}}=$
	$={\frac {1}{2}}{{r^{2}}\arcsin \left({1}\right)}+{\frac {1}{2}}{r{\sqrt {0}}}-{\frac {1}{2}}{{r^{2}}\arcsin \left({-1}\right)}+{\frac {1}{2}}{r{\sqrt {0}}}=$
	$={\frac {1}{2}}{r^{2}}{\frac {\pi }{2}}+0+{\frac {1}{2}}{r^{2}}{\frac {\pi }{2}}+0=$
	$={\frac {1}{2}}{\pi }{r^{2}}$

Per arrivare alla formula finale ricordiamo che fin dal principio stavamo calcolando l'area tra ilgraficodella semicirconferenza$y={\sqrt {r^{2}-x^{2}}}$e l'asse$x$,per cui l'area del cerchio con centro nell'origine sarà il doppio:

$2\cdot {\frac {1}{2}}{\pi }{r^{2}}={\pi }{r^{2}},$

che è proprio la formula usata comunemente.

Dobbiamo notare che in questa dimostrazione diamo per definita la formula dell'arcoseno(per trovare unaprimitivadella funzione), e quindi buona parte dellatrigonometria;questo però significa inserire anche nei concetti necessari per usare questo metodo quello dipi greco,che è indissolubilmente legato al concetto di cerchio e alle relazioni tra le sue parti.

Il perimetro del cerchio

Il perimetro del cerchio si può calcolare con la formula$2\pi r$,cioè due volte ilpi grecoper il raggio.

Integrazione della semicirconferenza nel piano cartesiano

Il perimetro del cerchio, che si può definire anche come la lunghezza dellacirconferenza,si può pensare calcolabile grazie all'integrazione della funzione corrispondente alla semicirconferenza, avente centro nell'origine, tra$-r$e$r$,cioè il raggio. Ovviamente non possiamo utilizzare l'integrale definito, ma ci serve l'integrale che associa ad una funzione la lunghezza della curva che descrive: la formula di questo integrale, data una funzione$f(x)$e due punti$a$e$b$è:

$\int _{a}^{b}{\sqrt {1+\left({\dot {f}}(x)\right)^{2}}}\,dx.$

Sappiamo che l'equazione di una circonferenza di generico raggio$r$e centro nell'origine degli assi è:

$x^{2}+y^{2}=r^{2}.$

Questa, come visto per l'area, va resa una funzione, e per farlo basta dopo averla esplicitata in funzione di$y$,$y=\pm {\sqrt {r^{2}-x^{2}}}$,prenderne solo le immagini non negative.

L'equazione della funzione che descrive la semicirconferenza che ci serve sarà allora

$y={\sqrt {r^{2}-x^{2}}}.$

Per calcolare l'integrale ci serve però laderivataprima della funzione stessa, quindi:

$y'={\frac {-2x}{2{\sqrt {r^{2}-x^{2}}}}}={\frac {-x}{\sqrt {r^{2}-x^{2}}}}.$

Adesso possiamo procedere al calcolo dell'integrale della curva tra$-r$e$r$.Svolgiamo quindi i calcoli, ricorrendo come prima alteorema di Torricelli-Barrow:

$\int _{-r}^{r}{\sqrt {1+\left({\frac {-x}{\sqrt {r^{2}-x^{2}}}}\right)^{2}}}\,dx$	$=\left[\int \ {\sqrt {1+{\frac {x^{2}}{r^{2}-x^{2}}}}}\right]_{-r}^{r}=$
	$=\left[\int \ {\sqrt {\frac {r^{2}-x^{2}+x^{2}}{r^{2}-x^{2}}}}\right]_{-r}^{r}=$
	$=\left[\int \ {\sqrt {\frac {r^{2}}{r^{2}-x^{2}}}}\right]_{-r}^{r}=$
	$=\left[\int \ {\frac {r}{\sqrt {r^{2}-x^{2}}}}\right]_{-r}^{r}=$
	$=\left[\int \ {\frac {r}{r{\sqrt {1-{\frac {x^{2}}{r^{2}}}}}}}\right]_{-r}^{r}=$
	$=\left[\int \ {\frac {1}{\sqrt {1-{\frac {x^{2}}{r^{2}}}}}}\right]_{-r}^{r}=$
	$=\left[r\arcsin \left({\frac {x}{r}}\right)\right]_{-r}^{r}=$
	$=r\arcsin \left({\frac {r}{r}}\right)-r\arcsin \left({\frac {-r}{r}}\right)=$
	$=r\arcsin \left(1\right)-r\arcsin \left(-1\right)=$
	$=r{\frac {\pi }{2}}+r{\frac {\pi }{2}}=$
	$=2\cdot {\frac {\pi r}{2}}={\pi r}$

Ma dal momento che stavamo calcolando la lunghezza di una semicirconferenza, allora il perimetro del cerchio sarà pari al doppio del valore trovato, cioè:

$2\cdot \pi r=2\pi r.$

Ed è esattamente il valore che viene utilizzato solitamente.

Come per il calcolo dell'area, dobbiamo ricordare che per la dimostrazione è essenziale conoscere la trigonometria, che implica di fatto la conoscenza del valore dipi grecoe il suo legame con le componenti di un cerchio. In pratica quindi quella che abbiamo fatto più che una dimostrazione è una riprova della formula che lega il raggio e la lunghezza di una circonferenza qualunque.

Cerchio, letteratura e filosofia

La figura del cerchio e del circolo è al centro dell'opera diPlatone.Leonardo da Vincipreferì invece collocare al centro della natura la figura della spirale. Lo stesso feceRalph Waldo Emerson,introducendo nel suo saggio sui "Cerchi" la figura di cerchi in espansione come simbolo dell'avanzamento dello spirito umano.

Angoli particolari nel cerchio

L'angolo alla circonferenza che sottende un diametro dello stesso cerchio è sempre retto

Angolo al centro

Si definisce 'angolo al centro' l'angolo che ha per vertice il centro della circonferenza e per lati due semirette che intersecano la circonferenza.Il cerchio è quindi diviso in due parti da ogni suo angolo al centro.

La sua ampiezza si calcola con la seguente proporzione:

$AB:C=a^{\circ }:360^{\circ }.$

Proprietà

L'angolo al centro è sempre il doppio del corrispondente angolo alla circonferenza, quando i vertici dell'angolo al centro e dell'angolo alla circonferenza sono dalla stessa parte rispetto alla corda individuata dai due punti di intersezione dei lati dei due angoli con la circonferenza. Quando invece il vertice dell'angolo alla circonferenza è dalla parte opposta rispetto al centro, l'angolo alla circonferenza è supplementare della metà dell'angolo al centro, cioè la somma dell'angolo alla circonferenza e la metà dell'angolo al centro è uguale ad unangolo piatto.Di conseguenza, se un angolo alla circonferenza è retto, esso sottende un diametro del cerchio, ovvero il corrispondente angolo al centro è piatto. Da ciò discendono le seguenti proprietà deltriangolo rettangolo:

• ogni triangolo rettangolo è inscrivibile in un semicerchio;
• in ogni triangolo rettangolo, l'ipotenusa coincide con un diametro del cerchio circoscritto.

Formulario

Formule geometriche

Data una circonferenza, siano$r$il raggio,$A$l'area,$d=2r$il diametro,$P$il perimetro. Allora si ha:

Raggio$r={\frac {d}{2}}={\frac {P}{2\pi }}={\sqrt {\frac {A}{\pi }}};$

Perimetro$P=2\pi r=d\pi =2{\sqrt {\pi A}};$

Area$A=\pi r^{2}={\frac {\pi }{4}}d^{2}={\frac {P^{2}}{4\pi }}.$

Formule analitiche

Avendo le coordinate del centro$(x_{0},y_{0})$e di un punto sulla circonferenza$(x_{i},y_{i})$è possibile determinare l'area

Raggio	${\sqrt {(x_{0}-x_{i})^{2}+(y_{0}-y_{i})^{2}}},$
Area	$\pi \left[(x_{0}-x_{i})^{2}+(y_{0}-y_{i})^{2}\right].$

Date invece lecoordinatedi tre punti$A$,$B$,$C$qualsiasi sulla circonferenza le coordinate del centro si calcolano come quelle delcircumcentrodel triangolo

$x_{0}={\frac {b_{x}}{-2a}};\quad y_{0}={\frac {b_{y}}{-2a}},$

con

$b_{x}=-{\begin{vmatrix}x_{A}^{2}+y_{A}^{2}&y_{A}&1\\x_{B}^{2}+y_{B}^{2}&y_{B}&1\\x_{C}^{2}+y_{C}^{2}&y_{C}&1\\\end{vmatrix}};\quad b_{y}={\begin{vmatrix}x_{A}^{2}+y_{A}^{2}&x_{A}&1\\x_{B}^{2}+y_{B}^{2}&x_{B}&1\\x_{C}^{2}+y_{C}^{2}&x_{C}&1\\\end{vmatrix}};\quad a={\begin{vmatrix}x_{A}&y_{A}&1\\x_{B}&y_{B}&1\\x_{C}&y_{C}&1\\\end{vmatrix}}.$

Voci correlate

• Circonferenza
• Quadratura del cerchio
• Settore circolare
• Corona circolare
• Segmento circolare
• Sfera
• Intorno circolare

Altri progetti

Altri progetti

• Wikiquote
• Wikizionario
• Wikimedia Commons

• Wikiquotecontiene citazioni di o sucerchio
• Wikizionariocontiene il lemma di dizionario «cerchio»
• Wikimedia Commonscontiene immagini o altri file sucerchio

Collegamenti esterni

• (EN) Eric W. Weisstein,Cerchio,suMathWorld,Wolfram Research.

Controllo di autorità	Thesaurus BNCF11846·GND(DE)4406111-0