Numero primo

La distribuzione dei numeri primi (linee blu) fino a 400

Inmatematica,unnumero primo(in breve ancheprimo) è unnumero interopositivo che abbia esattamente duedivisoridistinti. In modo equivalente si può definire come unnumero naturalemaggiore di 1 che siadivisibilesolamente per1e per sé stesso; al contrario, un numero maggiore di 1 che abbia più di due divisori è dettocomposto.Ad esempio 2, 3 e 5 sono primi mentre 4 e 6 non lo sono perché sono divisibili rispettivamente anche per 2 e per 2 e 3. L'unico numero primopariè 2, in quanto tutti gli altri numeri pari sono divisibili per 2.

Lasuccessionedei numeri primi comincia con2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,139…

Quello di numero primo è uno dei concetti basilari dellateoria dei numeri,la parte della matematica che studia inumeri interi:l'importanza sta nella possibilità di costruire con essi, attraverso la moltiplicazione, tutti gli altri numeri interi, nonché l'unicità di talefattorizzazione.I primi sono inoltreinfinitie la loro distribuzione è tuttora oggetto di molte ricerche.

I numeri primi sono oggetto di studio fin dall'antichità: i primi risultati risalgono agliantichi Greci,e in particolare agliElementidiEuclide,scritti attorno al300 a.C.Ciononostante, numerosecongettureche li riguardano non sono state ancoradimostrate;tra le più note vi sono l'ipotesi di Riemann,lacongettura di Goldbache quelladei primi gemelli,indimostrate a più di un secolo dalla loro formulazione.

Essi sono rilevanti anche in molti altri ambiti della matematica pura, come ad esempio l'algebrao lageometria;recentemente hanno assunto un'importanza cruciale anche nella matematica applicata, e in particolare nellacrittografia.

Storia

Non è noto quando sia stato definito il concetto di numero primo, tuttavia un segnale che fa supporre una qualche consapevolezza della diversità di tali numeri è testimoniato dall'Osso d'Ishango,un reperto osseo datato alPaleolitico superiore,in cui compaiono dei segni rappresentanti i numeri primi compresi tra 10 e 20. Per trovare un altro segno di questa consapevolezza bisogna recarsi inMesopotamiae aspettare ilsecondo millennio a.C.;a tale periodo appartengono infatti alcune tavolette contenenti le soluzioni di alcuni problemi aritmetici che, per essere svolti, richiedono una buona conoscenza della fattorizzazione in primi.Allo stesso millennio appartiene anche ilpapiro di Rhind(trascritto intorno al1650 a.C.), che contiene alcune espansioni infrazioni egiziedei numeri nella forma²⁄_n.Le espansioni dei numeri che hanno in comune il più piccolo dei loro fattori sono simili, suggerendo che gliEgizifossero almeno consapevoli della differenza tra i numeri primi e i composti.

Un frammento degliElementidi Euclide rinvenuto aOssirinco.

La prima traccia incontestabile di un vero studio dei numeri primi è costituita dagliElementidiEuclide,un libro composto tra ilIVe ilIII secolo a.C.,che fornisce un quadro completo delle conoscenze matematiche del tempo. Quest'opera contiene alcuni risultati fondamentali, tra cui ilteorema dell'infinità dei primie illemma di Euclide,che prova un'importante caratterizzazione dei numeri primi.Euclide dimostra anche la possibilità difattorizzareogni intero positivo come prodotto di primi.All'antica Grecia dobbiamo anche ilcrivello di Eratostene,un semplicealgoritmoper determinare quali sono i numeri primi.

Pierre de Fermat

I secoli seguenti registrarono un certo disinteresse per lo studio dei numeri primie per diverso tempo non furono dimostrati risultati di particolare rilevanza su questo argomento. L'interesse verso di essi riprese vigore neldiciassettesimo secolo,con le dimostrazioni di nuovi e importanti risultati, alcuni dei quali dovuti aPierre de Fermat:in particolare egli provò un teorema sullecongruenze modulo un primo,noto come "piccolo teorema di Fermat",e ilteorema sulle somme di due quadratiche afferma che tutti i primi di una certa forma si possono scrivere come somma di due quadrati. Congetturò inoltre che tutti i numeri nella forma 2²ⁿ+ 1 (oggi chiamati in suo onorenumeri di Fermat) fossero primi; Fermat stesso aveva verificato la sua congettura fino an= 4, maEuleromostrò che pern= 5 si otteneva un numero composto. A oggi non sono noti altri numeri di questo tipo che siano primi. Nello stesso periodo, il monaco franceseMarin Mersennepose l'attenzione sui primi nella forma 2^p− 1, conpprimo, che oggi sono chiamati in suo onoreprimi di Mersenne.

Altri risultati vennero ottenuti da Eulero nel corso deldiciottesimo secolo:tra di essi vi sono ladivergenzadellaserieinfinita¹⁄₂+¹⁄₃+¹⁄₅+¹⁄₇+¹⁄₁₁+..., in cui gli addendi sono gli inversi dei numeri primi, e il cosiddettoprodotto di Eulero,una formula che evidenzia il legame dei primi con laserie armonica.Nella corrispondenza di Eulero conChristian Goldbach,quest'ultimo formulò inoltre la famosacongettura di Goldbach,ancora oggi non dimostrata, che riguarda la rappresentazione dei numeri naturali pari come somma di numeri primi.

Dall'inizio dell'Ottocento,l'attenzione di molti matematici si rivolse allo studio della distribuzioneasintoticadei primi, ossia allo studio dell'andamento della funzione che conta i primi minori o uguali ax.LegendreeGausscongetturarono indipendentemente che tale funzionetende,al crescere dix,ax/ ln(x), dove ln(x) indica illogaritmo naturaledix.Nel1859Bernhard Riemanncollegò questo problema con il posizionamento degli zeri dellafunzione zeta di Riemann,unafunzione di variabile complessa;questo approccio portò alla dimostrazione della congettura, compiuta in modo indipendente daHadamardede la Vallée Poussinnel1896.Tale risultato è oggi noto col nome diteorema dei numeri primi.

I numeri primi restarono confinati nell'ambito della matematica pura fino aglianni settanta,quando venne sviluppato il concetto dicrittografia a chiave pubblica;il primo algoritmo di questo tipo, l'RSA,sfrutta infatti la difficoltà difattorizzarenumeri grandi formati da due soli fattori primi. Per questo motivo, ha assunto una notevole importanza anche la ricerca di numeri primi sempre più grandi. A partire dal1951,tale ricerca viene effettuata attraverso l'uso dicomputer.

Prime proprietà

Applicazione delcrivello di Eratosteneper trovare i numeri primi minori o uguali a 120.

Il più piccolo numero primo è 2; tutti gli altri sonodispari,in quanto ogni numero pari è divisibile per 2. Nel passato 1 era a volte considerato un numero primo: ad esempioDerrick Norman Lehmerlo incluse nella sua tavola dei numeri primi pubblicata nel1914.Oggi tuttavia si preferisce escluderlo, in quanto il suo inserimento tra i primi costringerebbe a riformulare in maniera più complessa diversi teoremi (come ilteorema fondamentale dell'aritmetica) per tenere conto di questo caso speciale.

Un metodo per verificare se un numeronè primo si definiscetest di primalità.Un metodo che discende direttamente dalla definizione è controllare che non sia diviso da nessun numero minore dino, in modo più efficiente, da nessun primo minore din.Ad esempio, per provare che 11 è primo, basta osservare che non è diviso da 2, 3, 5 e 7 (che sono i primi minori di 11).

Rappresentazione di 12 come rettangolo e tentativi di rappresentare 11 in questo modo.

Un antico algoritmo che evita le divisioni è ilcrivello(ossiasetaccio) diEratosteneche, più precisamente, determina l'insiemedei primi minori o uguali aX.Per far ciò, l'algoritmo parte dall'insieme dei numeri naturali compresi tra 2 eX,ed elimina imultiplidei numeri primi individuati in precedenza (perché non sono multipli di numeri più piccoli).In effetti, è possibile migliorare questo algoritmo fermandosi a eliminare i multipli dei primi minori o uguali allaparte interadellaradicediX:se infatti un numero compostocha tutti i fattori maggiori della radice diX,allora è maggiore diX,in quanto, dovendo avere almeno due fattori,

$c>{\sqrt {X}}{\sqrt {X}}=X.$

La figura a destra mostra il funzionamento dell'algoritmo perX= 120. Analogamente, se si utilizza il metodo delle divisioni per dimostrare la primalità di un numeroXsi può evitare di controllare la divisibilità diXper numeri maggiori della radice quadrata diX.

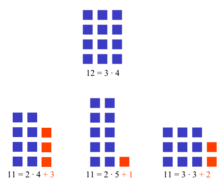
In una semplice interpretazione geometrica del concetto di numero primo, i numerinche non sono primi sono esattamente quei numeri che possono essere rappresentati come rettangoli composti danquadratini i cui lati sono maggiori di 1. Ad esempio 12 non è primo, perché può essere rappresentato come un rettangolo di lati 3 e 4, mentre 11 è primo, perché non ammette nessuna rappresentazione di questo tipo. Ogni rappresentazione di un numero composto tuttavia ne ammette una simmetrica a seconda che il lato lungo sia orizzontale o verticale; arrestare il crivello (o le divisioni) una volta raggiunta la radice diXsignifica considerare solo un rettangolo per ciascuna coppia di rettangoli simmetrici.

Scomposizione in fattori primi

L'importanza dei numeri primi in matematica è enorme e deriva essenzialmente dalteorema fondamentale dell'aritmetica,il quale asserisce che qualsiasi numero intero positivo diverso da 1 può essere scomposto in fattori primi, e tale scomposizione è unica a meno dell'ordine dei fattori.

Ad esempio, 23244 si fattorizza come

$23244=2^{2}\times 3\times 13\times 149$

e ogni altra sua fattorizzazione in numeri primi è ottenuta da questapermutandoi fattori. Ad esempio, l'ulteriore fattorizzazione

$23244=13\times 3\times 2\times 149\times 2$

non è altro che quella precedente con i fattori scritti in un ordine diverso. A causa di questa proprietà, ci si riferisce a volte ai numeri primi come agli "atomidell'aritmetica ".

Questa è tra l'altro la ragione principale per cui 1 è escluso dall'insieme dei primi. Infatti, se si moltiplica una fattorizzazione di un numero per uno, un numero di volte a piacere, si ottiene sempre il numero di partenza, creando così fattorizzazioni distinte.

Una proprietà strettamente collegata alla fattorizzazione unica è illemma di Euclide:se un primopdivide il prodottoab,allora divideaoboppure siaacheb.Questa è considerata la definizione stessa dielemento primoin undominio d'integrità,ed è ovvia a partire dal teorema fondamentale dell'aritmetica: la fattorizzazione diabdovrà infatti contenere il primop,e visto chepnon può essere "spezzato" in due fattori, deve necessariamente essere nella fattorizzazione di almeno uno dei due numeri.

Infinità

I numeri primi sono infiniti. La più antica dimostrazione pervenutaci è quella diEuclide,che la presenta nel IX libro degliElementi,come proposizione 20, con le parole:

«I numeri primi sono più di una qualsiasi assegnata moltitudine di numeri primi.»

La dimostrazione procedeper assurdo.Supponendo infatti che esista solo un numero finito di numeri primip₁,p₂,...,p_n,si può considerare il numeroq=p₁p₂···p_n+ 1: questo numero è ovviamente maggiore di 1 e diverso da tutti i numeri primip_i.Ora, vi sono due possibilità perq:può essere primo o composto. Se fosse primo avremmo però una contraddizione, perché abbiamo assunto che ip_isiano tutti i numeri primi; se fosse invece composto, dovrebbe avere un fattore primod,che deve essere uno dei numeri primip_i.Ma alloraddivide siaqsia il prodottop₁p₂···p_n(essendo uno dei numeri primi), e quindi deve dividere la loro differenzaq−p₁p₂···p_n= 1, il che è impossibile. Quindiqnon può essere né primo né composto: ma questo è assurdo, e i numeri primi sono infiniti.

Una questione che sorge dalla dimostrazione è se i numeri nella formap₁p₂···p_n+ 1, cioè il prodotto dei priminprimi più 1 (dettinumeri di Euclide), siano o meno primi. Questo avviene nei primi casi (2·3 + 1 = 7 è primo, così come 2·3·5 + 1 = 31), ma è falso in generale: il più piccolo di tali numeri a essere composto è

$2\cdot 3\cdot 5\cdot 7\cdot 11\cdot 13+1=30031=59\cdot 509.$

Non è noto se in questa successione esistano infiniti numeri primi, anche se è stato congetturato che sia così.

Molte altre dimostrazioni sono state create nel corso dei secoli:Eulerodimostrò questo teorema a partire dalladivergenzadellaserie armonica,Goldbachattraverso inumeri di Fermat,mentreHarry Furstenbergne ideò una usando metodi dellatopologia.

Un teorema più forte, da cui si ricava facilmente l'infinità dei numeri primi, è quello che stabilisce che laserie1/2+1/3+1/5+1/7+1/11+...,formata dalla somma degli inversi dei numeri primi,diverge,e in particolare, usando la notazioneO-grande:

$\sum _{p\leq n}{\frac {1}{p}}=\ln \ln n+O(1).$

Questo teorema è dovuto a Eulero, che lo dimostrò nel diciottesimo secolo.

Dalla dimostrazione di Euclide segue anche che

$p_{n+1}<p_{1}p_{2}\cdots p_{n}.$

Tale disuguaglianza può essere migliorata: H. Bonse dimostrò nel 1907 (disuguaglianza di Bonse) che

$p_{n+1}^{2}<p_{1}p_{2}...p_{n}$

pern> 3. Su questa strada, è stato dimostrato che la disuguaglianza

$p_{n+1}^{k}<p_{1}p_{2}...p_{n}$

è verificata per ognin> 2k- 1.

Distribuzione dei numeri primi

Comparazione tra le funzioni π(x) (blu),x/ lnx(verde) e Li(x) (rosso), si può notare che l'approssimazione di π(x) con Li(x) risulta essere di gran lunga migliore di quella conx/ lnx

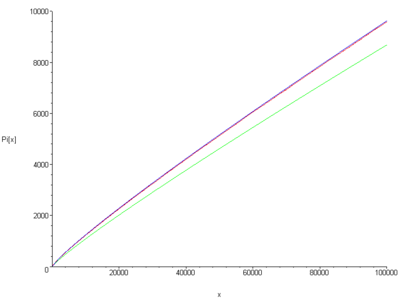
Una volta dimostrato che i numeri primi sono infiniti, sorge spontaneo chiedersi come si distribuiscono all'interno della sequenza dei numeri naturali, cioè quanto sono frequenti e quando ci si può aspettare di trovare l'n-esimo numero primo. Questo studio fu incominciato verso la fine delXVIII secoloindipendentemente daGausse daLegendre,che introdussero la funzione$\pi (x)$(dettafunzione enumerativa dei primi) e congetturarono che essa fosse approssimativamente

$\pi (x)\sim {\frac {x}{\ln x}}.$

Il tentativo di dimostrare questa congettura attraversò tutto l'Ottocento; i primi risultati furono ottenuti tra il1848e il1859daČebyšëv,che dimostrò usando metodi puramentearitmeticiche esistevano due costantiAeBtali che

$A\leq {\frac {\pi (x)}{\frac {x}{\ln x}}}\leq B$

perxsufficientemente grande.Riuscì anche a provare che, se illimitedel rapporto esiste, allora esso deve essere 1.

Una dimostrazione fu invece trovata nel1896daHadamarde dade la Vallée-Poussin,che, pur lavorando indipendentemente l'uno dall'altro, usarono metodi simili, basati sull'uso dellafunzione zeta di Riemann,la quale era stata introdotta daBernhard Riemannnel1859.Per una dimostrazione che usasse soltanto metodi elementari (cioè senza usare metodi dianalisi complessa) si dovette attendere invece fino al1949,quando essa fu ideata daSelbergeErdős.Il teorema è oggi noto cometeorema dei numeri primi.

Confronto tra l'n-esimo numero primo (in blu) en· lnn(in rosso), perntra 0 e 10000.

Gauss aveva introdotto anche una stima più precisa, utilizzando la funzionelogaritmo integrale:

$\pi (x)\sim {\frac {}{}}\mathrm {Li} (x)=\int _{2}^{x}{\frac {1}{\ln u}}\mathrm {d} u.$

Nel1899de la Vallée-Poussin dimostrò che l'errore che si commette approssimando$\pi (x)$in questo modo è

$\pi (x)-\mathrm {Li} (x)=O\left(x\mathrm {e} ^{-a{\sqrt {\ln x}}}\right)=O\left({\frac {x}{(\ln x)^{m}}}\right)$

per una costante positivaae ogni interom;tale risultato è stato leggermente migliorato nel corso degli anni.Inoltre, nel1901von Kochmostrò che se l'ipotesi di Riemannè vera, allora si ha la stima molto più precisa:

$\pi (x)-\mathrm {Li} (x)=O\left({\sqrt {x}}\ln x\right).$

Una forma equivalente al teorema dei numeri primi è chep_n,l'n-esimo numero primo, è ben approssimato danln(n). In effetti,p_nè strettamente maggiore di questo valore, come è stato dimostrato daJ. Barkley Rossernel1938;questa disuguaglianza è stata migliorata fino ad arrivare, nel 1995, a

$p_{n}>n(\ln n+\ln \ln n-1),~$

pern≥ 2.

Intervalli tra i numeri primi

La distribuzione dei primi gemelli pern≤100 000

Legato alla distribuzione dei numeri primi è lo studio degli intervalli tra due primi consecutivi. Questo, a parte la coppia formata da 2 e 3, deve essere necessariamente un numero pari maggiore o uguale a 2, perché tra due numeri consecutivi almeno uno è pari e quindi non primo. Se due numeri primi hanno come differenza 2, sono dettigemelli:con l'eccezione della "tripletta" formata da 3, 5 e 7, i numeri primi gemelli si presentano a coppie, ed è semplice verificare che, tranne nel caso 3 e 5, il numero posto tra di loro è sempre un multiplo di 6. Le più piccole coppie di primi gemelli sono (3, 5), (5, 7), (11, 13), (17, 19) e (29, 31). È stato congetturato che esistano infinite coppie di numeri primi gemelli, sebbene nessuno sia ancora riuscito a dimostrarlo; un'estensione di questa idea è chiedersi se, dato un numero parik,la differenza tra due primi consecutivi sia pari akinfinite volte. Quest'ultimo problema prende il nome dicongettura di Polignac.

È facile invece mostrare che questa differenza può essere grande a piacere: dato un interoN,e indicando conN!il suofattoriale(cioè il prodotto di tutti i numeri compresi tra 1 eN), i numeri

$(N+1)!+2,~(N+1)!+3,\cdots,(N+1)!+N+1$

sono tutti composti: infatti, semè minore diN,allora (N+ 1)! +mè divisibile perm,e quindi non è primo. La sequenza, che comprendeNnumeri consecutivi, è quindi priva di numeri primi. Ad esempio, seN= 5, questi valori corrispondono a

$6!+2=722=2\times 361$

$6!+3=723=3\times 241$

$6!+4=724=4\times 181$

$6!+5=725=5\times 145$

$6!+6=726=6\times 121$

mentre il valore successivo, 6!+7=727, è primo.Si noti comunque che esistono modi più "efficienti" per costruire intervalli senza numeri primi; ad esempio invece di (N+ 1)! + 1 si può considerare il prodotto dei numeri primi minori diN+ 2.

Dal teorema dei numeri primi discende facilmente che l'intervalloattesotra due numeri primi consecutivip_nep_n+1ha lunghezza ln(p_n); tuttavia questi intervalli sono talvolta molto più grandi e talvolta molto più piccoli. Sugli intervalli corti, lacongettura dei primi gemelliafferma esattamente che l'intervallo è il minimo possibile infinite volte. Questa congettura è tuttora aperta, ma grazie al lavoro diZhang Yitang(annunciato nel 2013, e basato sull'approccio diGoldston,PintzeYıldırım) e ai successivi contributi diJames Maynarde di unprogetto Polymath,è noto che esistono infiniti numeri primi consecutivi la cui differenza è minore di 246.

Sul problema opposto, degli intervalli lunghi, ci si aspetta che tali intervalli siano di ordine ln²p_n,o, più precisamente, che

$0<\limsup _{n\rightarrow \infty }{\frac {p_{n+1}-p_{n}}{\ln ^{2}n}}\ll 1,$

mentre i migliori risultati dimostrati sono

$\limsup _{n\rightarrow \infty }{\frac {p_{n+1}-p_{n}}{\ln p_{n}(\ln \ln p_{n})(\ln \ln \ln \ln p_{n})/\ln \ln \ln p_{n}}}>0$

e

$p_{n+1}-p_{n}=O\left(p_{n}^{\frac {21}{40}}\right),$

dovuti rispettivamente aFord,Green,Konjagin,Maynard eTaoe a Pintz.

Un altro risultato classico, seppur più debole di quelli appena riportati, è ilpostulato di Bertrand(che in realtà è un teorema, essendo stato dimostrato daČebyšëvnel1850). Esso afferma che per ogninesiste sempre un primo trane 2n.Un'interessante conseguenza di questo risultato è chep_n+1< 2p_n;considerando inoltre chep₁= 2 si deduce facilmente che per ogninvale la disuguaglianza

$p_{n}<2^{n}.$

Nel corso dei secoli, sono state proposte molte congetture sugli intervalli tra primi consecutivi. Le più famose sono lacongettura di Legendre,che afferma che tra due quadrati consecutivi vi è sempre un primo, lacongettura di Brocardche asserisce che tra i quadrati di due primi dispari consecutivi esistono sempre quattro numeri primi, e lacongettura di Andricache ipotizza che

${\sqrt {p_{n+1}}}-{\sqrt {p_{n}}}<1.$

Queste congetture sono tutte molto più deboli di quanto ritenuto comunemente vero, ma sono tuttora indimostrate. I migliori risultati in questa direzione sono la dimostrazione che tran²e (n+ 1)²giace sempre almeno un primo o unsemiprimo,dovuta aChen Jingrun,e il risultato di Baker, Harman e Pintz riportato sopra.

Rapporti con gli altri campi della matematica

Essendo alle basi dell'aritmetica,i numeri primi sono ingredienti fondamentali in un gran numero di settori della matematica.

Funzioni aritmetiche

Lefunzioni aritmetiche,ossia le funzioni definite sugli interi e a valori neinumeri complessi,rivestono un ruolo cruciale nellateoria dei numeri.In modo particolare, tra queste le più importanti sono lefunzioni moltiplicative,ovvero quelle funzionifin cui, per ogni coppia (a,b) di numericoprimi,si ha

$f(ab)=f(a)f(b).$

Esempi di funzioni moltiplicative sono lafunzione φ di Eulero,che anassocia il numero degli interi che sono al contempo minori e coprimi conn,e le funzionidivisoreesigma,che anassociano rispettivamente il numero dei suoi divisori e la loro somma. Il valore di tali funzioni nelle potenze dei primi è

• funzione φ di Eulero:$\operatorname {\varphi } (p^{m})=p^{m}-p^{m-1},$
• funzione divisore:$d(p^{m})=m+1,$
• funzione sigma:$\operatorname {\sigma } (p^{m})=1+p^{1}+p^{2}+p^{3}+\cdots +p^{m}.$

Grazie alla proprietà che le definisce, le funzioni aritmetiche si possono facilmente calcolare conoscendo il valore che esse assumono nellepotenzedei primi. Infatti, dato un interondi fattorizzazione

$n=p_{1}^{q_{1}}\cdots p_{a}^{q_{a}},$

si ha che

$f(n)=f(p_{1}^{q_{1}})\cdots f(p_{a}^{q_{a}})$

e dunque si è ricondotto il problema di calcolaref(n) a quello di calcolarefsulle potenze dei primi che dividonon,valori che sono in genere più semplici da ricavare rispetto a una formula generale. Ad esempio, per conoscere il valore della funzione φ di Eulero sun= 450 = 2×3²×5²è sufficiente calcolare

$\operatorname {\varphi } (450)=\operatorname {\varphi } (2)\cdot \operatorname {\varphi } (3^{2})\cdot \operatorname {\varphi } (5^{2})=(2-1)\cdot (9-3)\cdot (25-5)=120.$

Il fatto che una funzione moltiplicativa sia individuata dai valori assunti in corrispondenza delle potenze dei numeri primi è all'origine dell'uso delleserie di Bell,che sono delle particolariserie formali di potenze.Data una funzione moltiplicativafe un primop,la serie di Bell difrispetto apè:

$f_{p}(x)=\sum _{n=0}^{\infty }f(p^{n})x^{n}.$

In particolare, sefècompletamentemoltiplicativa (cioè sef(ab) =f(a)f(b) per ogniaeb), allorafè individuata dai valori dif(p), perpprimo, e la sua serie di Bell è:

$f_{p}(x)=\sum _{n=0}^{\infty }f(p)^{n}x^{n}={\frac {1}{1-f(p)x}}.$

Aritmetica modulare

Nell'aritmetica modularei numeri primi svolgono un ruolo molto importante: l'anello$\mathbb {Z} /n\mathbb {Z}$delle classi di resto è infatti uncampose e solo senè primo. In questo caso lo studio delle classi di resto è più semplice del caso generale, e fornisce un'utile base di partenza per l'analisi delle classi di resto connqualunque.

Anche l'esistenza di unaradice primitivadell'anello$\mathbb {Z} /n\mathbb {Z}$è legata ai numeri primi: questa infatti esiste solamente senè un numero primo, 1, 2, 4 oppure un numero nella forma$p^{n}$o$2p^{n}$,dovepè un primo dispari.

Uno dei teoremi più importanti dell'aritmetica modulare è costituito dalpiccolo teorema di Fermat.Tale teorema afferma che, per ogni primope ogni numero naturaleasi ha

$a^{p}\equiv a\mod p.$

Equivalentemente, per ogni primope ogni interoacoprimoconp,si ha

$a^{p-1}\equiv 1\mod p.$

Questa proprietà può essere usata per verificare se un numerononè primo, infatti senè tale che

$a^{n}\not \equiv a\mod n$

per qualche interoa,allorannon può essere primo. Tuttavia questa proprietà non può essere usata per controllare se un numero è primo: esistono infatti alcuni numeri, dettinumeri di Carmichael(il più piccolo dei quali è 561), che verificano questa proprietà per ogniapur non essendo primi. Nel1994,William Robert Alford,Andrew GranvilleeCarl Pomerancehanno dimostrato che vi sono infiniti numeri di tale tipo.

Numerip-adici

Un altro degli argomenti principali dellateoria dei numeriè costituito dallo studio dei numerip-adici e delle loro proprietà. Tali numeri sono definiti nel modo seguente: per ogni primopsi considera unanormasuinumeri razionali$\mathbb {Q}$che, valutata su un numero razionaleq,assume valori che si avvicinano allo 0 al crescere della massima potenza dipche divideq.Tale norma è detta "normap-adica ".Completandoil campo dei numeri razionali rispetto allametricaindotta da tale norma, si ottiene un campo, indicato con$\mathbb {Q} _{p}$,che "estende" inumeri razionaliin un modo diverso dainumeri reali.Gli elementi di tale campo sono dettinumerip-adici.Tali numeri si possono anche costruire comelimite proiettivodegli anelli$\mathbb {Z} /p\mathbb {Z},~\mathbb {Z} /p^{2}\mathbb {Z},~\mathbb {Z} /p^{3}\mathbb {Z} \ldots$.

Teoria dei gruppi

I numeri primi hanno un ruolo centrale anche nell'algebra.Nellateoria dei gruppi,ungruppoin cui ogni elemento haordinela potenza di un primopè dettop-gruppoogruppo primario.Tra igruppi finiti,ip-gruppi sono tutti e soli i gruppi la cuicardinalitàè la potenza di un primo; un esempio dip-gruppo infinito è ilp-gruppo di Prüfer.

È noto che ip-gruppi hanno uncentronon banale, e di conseguenza non possono esseresemplici(a parte il gruppo conpelementi); se il gruppo è finito, inoltre, tutti isottogruppi normaliintersecano il centro in modo non banale.

Tutti i gruppi con un numero primo di elementi sonociclicie dunqueabeliani;anche ogni gruppo di ordinep²è abeliano. Inoltre, ogni gruppo abeliano finito è isomorfo alprodotto direttodi un numero finito dip-gruppi ciclici.

Ilteorema di Cauchyafferma che, dato un gruppo di ordinene un primopche lo divide, esiste un elemento di ordinep,e quindi unsottogruppoconpelementi. Tale teorema è generalizzato daiteoremi di Sylow,che garantiscono che in ogni gruppo di ordinenesiste almeno un sottogruppo di ordinep^m,per ognip^mche dividen.

Teoria degli anelli e teoria dei campi

Nellateoria degli anelli,lacaratteristicadi undominio d'integritàDè 0 oppure un numero primo. Per uncampoF,che è un particolare tipo di dominio di integrità, la caratteristica determina ilsottocampo fondamentalediF:se essa è diversa da 0, e dunque è un numero primo, allora tale sottocampo è isomorfo al campo delle classi di resto$\mathbb {Z} /p\mathbb {Z}$.

Si mostra poi che tutti icampi finitiformano unospazio vettorialesul campo$\mathbb {Z} /p\mathbb {Z}$,e di conseguenza hanno un numero di elementi che è primo o è una potenza di un primo. Inoltre, due campi con lo stesso numero di elementi sonoisomorfi;in particolare, ogni campo con un numero primopdi elementi coincide con$\mathbb {Z} /p\mathbb {Z}$,mentre ogni campo conpⁿelementi è un'estensione di Galoisdi un campo conpelementi.

Tra le estensioni dei numeri razionali, un ruolo importante è svolto dalleestensioni ciclotomiche,ossia da quei campi che si possono ottenere aggiungendo a$\mathbb {Q}$leradicin-esime dell'unità,per un qualche numero naturalen.Ilgradodi queste estensioni è strettamente legato alla primalità din.Infatti esso èn− 1 se e solo senè primo: tale proprietà è equivalente al fatto che ilpolinomio

$P(x)=x^{n-1}+x^{n-2}+\cdots +x^{2}+x+1$

èirriducibiletra i polinomi a coefficientirazionalise e solo senè primo. Per una dimostrazione si può procedere come segue: senè composto (ad esempion=ab,conaebinteri maggiori di 1), lo si può dividere inagruppi dibaddendi, arrivando a una scomposizione. Ad esempio, sen= 10, prendendoa= 2 eb= 5,P(x) si può scomporre come

$x^{9}+x^{8}+\cdots +x^{2}+x+1=x^{8}(x+1)+x^{6}(x+1)+x^{4}(x+1)+x^{2}(x+1)+(x+1)=(x^{8}+x^{6}+x^{4}+x^{2}+1)(x+1).$

Per dimostrare l'inverso, si può usare invece ilcriterio di Eisenstein.Grazie a questa proprietà risulta inoltre che senè primo, allora questo polinomio coincide con l'n-esimopolinomio ciclotomico.

Polinomi e progressioni aritmetiche

È stato dimostrato daLegendrealla fine delSettecentoche nessunpolinomioa coefficienti interi può assumere valori soltanto primi: infatti, se esistesse un polinomioP(n) di questo tipo, si avrebbeP(1) = p per qualche primope quindiP(1) ≡ 0 modp.MaP(1) ≡P(1+kp) modpper ogni interok,e quindiP(1+kp) dovrebbe assumere infinite volte il valorep(perché i multipli dipnon possono essere primi). Tuttavia questo è assurdo, perché nessun polinomio può assumere uno stesso valore un numero di volte maggiore del proprio grado.

Alcuni polinomi sembrano assumere valori primi "più spesso" degli altri: ad esempioEuleronotò che il polinomio di secondo grado$n^{2}+n+41$produce numeri primi per ogni valore dincompreso tra 0 e 39; tuttavia, sebbene circa un terzo dei valori che questa funzione assume nei primi 10 milioni siano primi,non è stato ancora dimostrato che ne esistano infiniti. Più in generale, non c'è alcun polinomio in una sola variabile e di grado maggiore di uno di cui sia stato dimostrato che assume infiniti valori primi. Diversa è la situazione per i polinomi in due variabili: Dirichlet dimostrò che questo avviene per ogniforma quadratica$ax^{2}+bxy+cy^{2}$(a patto chea,becsiano coprimi e che la forma non sia il quadrato di un polinomio di primo grado),mentre nel1998John FriedlandereHenryk Iwanieclo provarono per il polinomio di quarto grado$x^{2}+y^{4}$.

Frazione dei numeri primicongruia 3 modulo 4.

A differenza di quanto accade per i polinomi di grado più alto,Dirichletdimostrò nel1837che ogni polinomio di primo gradoax+bassume infiniti valori primi se e solo seaebsono numeri naturali coprimi. Equivalentemente, unaprogressione aritmeticacontiene infiniti numeri primi se e solo se la suaragionee il suo primo valore sono coprimi. La prima dimostrazione di questo teorema, dettoteorema di Dirichlet,viene considerata la nascita dellaTeoria dei numeri analitica.

È noto inoltre che, seneksono coprimi, il rapporto traMe i primi minori diMche sono congrui akmodulontende a$1/\phi (n)$perMche tende all'infinito, ovvero i primi tendono a dividersi equamente tra le$\phi (n)$progressioni di ragionenche contengono più di un primo.

Sebbene non esistano progressioni aritmetiche i cui valori siano soltanto numeri primi, nel2004è stato dimostrato che esistono progressioni che contengono un numero arbitrariamente grande di termini consecutivi che sono primi (teorema di Green-Tao).Tale risultato è stato migliorato nel2006per includere anche le progressioni polinomiali; più precisamente è stato dimostrato che, dati dei polinomiP₁,...,P_ma coefficienti interi, esistono infiniti interiaemtali chea+P₁(n),...,a+P_m(n) sono contemporaneamente primi per 1 ≤n≤m.

Tali teoremi non sono tuttaviacostruttivi,ovvero non permettono di determinare esplicitamente delle progressioni arbitrariamente lunghe; la più lunga sequenza di primi (attualmente conosciuta) che sono termini consecutivi di una progressione aritmetica è composta da 26 numeri.È stato anche congetturato che esistano sequenze arbitrariamente lunghe di questo tipo tali che tra due termini della progressione non ci siano altri numeri primi, e la più lunga sequenza di primi di questo tipo finora trovata comprende 10 termini.

Una progressione aritmetica di interesse particolare per la teoria dei numeri primi è quella di ragione 4: si possono infatti separare i primi (a parte 2) in due gruppi, quelli nella forma 4k+1 e quelli nella forma 4k+3. Ilteorema di Fermat sulle somme di due quadratiasserisce che i primi che possono essere scritti come somma di duequadratisono tutti e soli quelli del primo gruppo. Un'importante riformulazione di questo teorema è che un primo è scomponibile nell'anellodegliinteri di Gaussse e solo se è della forma 4k+1.

Problemi additivi

Il numero di modi con cui un numeronsi può scrivere come somma di due primi pern≤1 000 000

Per la loro definizione, i numeri primi sono intrinsecamente legati all'operazionedi moltiplicazione. Tuttavia, sono di grande interesse anche alcuni problemi riguardanti loro proprietàadditive.

Il più famoso di questi è senza dubbio lacongetturaproposta daChristian GoldbachnelSettecento,che afferma che ogni numero pari maggiore di 2 può essere espresso come somma di due primi. La congettura è tuttora indimostrata, ma è facilmente verificabile per gli interi “piccoli”, come ad esempio

4 = 2 + 2

6 = 3 + 3

8 = 3 + 5

10 = 3 + 7 = 5 + 5

12 = 5 + 7

14 = 3 + 11 = 7 + 7,

e tramite l'uso di computer è stata controllata anche per tutti glinminori di 2×10¹⁸.

Alla congettura di Goldbach ne è legata un'altra, più debole e ora dimostrata, che afferma che ogni numero dispari è la somma di tre numeri primi. Questaex-congettura è comunemente nota con il nome dicongettura debole di Goldbach.

Mentre la congettura di Goldbach sembra molto lontana dall'essere risolta, la seconda ha conosciuto diversi progressi nel corso degli anni, culminati nella dimostrazione completa data daHarald Helfgottnel2013.In precedenza, risultati significativi erano stati ottenuti daHardyeLittlewood,che nel1923provarono che l'ipotesi di Riemann generalizzataimplica che ogni numero disparisufficientemente grandeè la somma di tre primi,e daIvan Vinogradovche nel1937dimostrò che l'assunzione dell'ipotesi di Riemann non è necessaria.Per completare la dimostrazione mancavano quindi solo un numero finito di numeri dispari da controllare,ma tale numero era ben al di là delle capacità computazionali dei moderni computer. Nel 2013, Helfgott introdusse diverse innovazioni all'interno della dimostrazione di Vinogradov, riuscendo ad abbassare notevolmente il numero di potenziali eccezioni a un numero effettivamente controllabile da un computer e quindi a completare la dimostrazione.

Sono noti anche altri risultati, sebbene molto più deboli. Usando ilpostulato di Bertrandsi può dimostrare che ogni intero maggiore di 6 può essere scritto come somma di primi distinti. Inoltre, sep_nè l'n-esimo numero primo, allora almeno uno trap_n,p_n− 1 ep_n+ 1 può essere scritto come

$\pm 2\pm 3\pm 5\cdots \pm p_{n-1}$

scegliendo opportunamente i segni "più" e "meno".

Problemi additivi sono considerati anche i già citatiteorema di Green-Taosulle progressioni aritmetiche, lacongettura dei primi gemellie lacongettura di Levy,che afferma che ogni intero dispari è la somma di un primo e di unsemiprimopari.

Principali problemi aperti

Molte congetture riguardanti i numeri primi non sono ancora state dimostrate. La più importante tra queste è senza dubbio l'ipotesi di Riemann,uno dei problemi aperti più importanti di tutta la matematica:era uno dei ventitréproblemi di Hilbert,enunciati nel1900,ed è stato inserito tra iproblemi per il millennionel2000.Nella sua formulazione originale, tale ipotesi riguarda il posizionamento degli zericomplessidellafunzione zeta di Riemann:nonostante il suo legame con i numeri primi non sia immediatamente chiaro, è stato provato che la sua dimostrazione avrebbe come conseguenza un notevole miglioramento della comprensione dei numeri primi. In particolare, se l'ipotesi di Riemann fosse vera, i primi sarebbero distribuiti nel modo più regolare possibile.

Altri problemi aperti molto famosi sono le già citate congetture diGoldbach,deiprimi gemellie diLegendre.

Altre congetture riguardano l'esistenza o meno di infiniti numeri primi in una certa forma. Ad esempio si pensa che esistano infiniti numeri primi nelle sequenzen²+ 1,2ⁿ- 1 (primi di Mersenne,OEIS:A000043),n!+ 1 en!- 1 (primi fattoriali,sequenzeOEIS:A002981eOEIS:A117141), o che esistano infiniti primi nellasuccessione di Fibonacci.Si congettura invece che vi siano solo un numero finito diprimi di Fermat,i numeri primi nella forma 2²ⁿ+ 1.Al momento, gli unici primi di Fermat noti sono in corrispondenza din= 0, 1, 2, 3 e 4.

Formule per i numeri primi

Una formula per i numeri primi è un'espressione che genera solamente numeri primi. Non sono note formule chiuse (che cioè non fanno ricorso né alimitiné aseriené a sommatorie la cui lunghezza dipenda dal dato iniziale) per trovare tutti i numeri primi fino an,o anche solo l'n-esimo primo; sono state invece trovate alcune formule che generano solo numeri primi, seppure fondamentalmente inutili dal punto di vista pratico. Un esempio è dato dalteorema di Millsche afferma che esiste unacostante θtale che

$\lfloor \theta ^{3^{n}}\rfloor$

è sempre un numero primo. Tuttavia non si conosce nessuna formula chiusa per calcolare la costante di Mills: le approssimazioni attualmente utilizzate si basano sulla sequenza dei cosiddetti primi di Mills (i numeri primi generati tramite questa formula), che non possono essere ricavati rigorosamente, ma solamente in maniera probabilistica, assumendo per vera l'ipotesi di Riemann.

A seguito della dimostrazione delteorema di Matiyasevich,sono stati trovati vari polinomi i cui valori positivi sono sempre numeri primi. Matijasevič dimostrò l'esistenza di un polinomio di 37º grado in 24 incognite, ma senza esplicitarlo; in seguito alcuni di questi sono stati determinati, ma rimangono poco utili per la ricerca di nuovi primi perché hanno diverse variabili e un grado molto elevato, e inoltre assumono spesso valori negativi.

Altre formule si possono costruire attraverso ilteorema di Wilsoncon l'uso della funzioneparte intera,ma anche queste sono sostanzialmente inutilizzabili a causa della loro elevatacomplessità computazionale.

Aspetti computazionali

Test di primalità

Untest di primalitàè unalgoritmoche permette di stabilire se un dato numero è primo oppure no. Nellateoria della complessità computazionale,questo problema è a volte denotato come PRIMES, ed è stato recentemente dimostrato appartenere allaclasse di complessitàP.

Il più antico e semplice test di primalità è quello di "divisione per tentativi", che consiste nell'applicare direttamente la definizione di numero primo: si prova a dividere il numeroNper tutti i numeri minori diN:se nessuno di questi lo divide, allora il numero è primo. Un semplice miglioramento di questo metodo si ottiene limitando i tentativi di divisione ai numeri primi minori di${\sqrt {N}}$.Sebbene molto semplice da descrivere e da implementare su un calcolatore, tale metodo è poco usato nella pratica, perché richiede tempi di calcolo che aumentanoesponenzialmenterispetto al numero delle cifre diN.Esso tuttavia fornisce anche i suoi fattori primi (ed è quindi un algoritmo difattorizzazione): questo non succede nel caso di algoritmi più sofisticati, che riescono a stabilire se un numero non è primo anche senza determinare alcun divisore non banale.

Altri algoritmi di primalità piuttosto semplici, ma poco utili dal punto di vista pratico, sono il test che si può ricavare dalcrivello di Eratostenee itest di Fermatedi Wilson,che si basano rispettivamente sulpiccolo teorema di Fermate sulteorema di Wilson.

Diversi altri algoritmi sono stati sviluppati nel corso del tempo: alcuni di essi si applicano solo a classi particolari di numeri, come ad esempio itest di Lucas-Lehmeredi Proth,che si applicano solo ainumeri di Mersenneedi Prothrispettivamente. Altri, come iltest di Miller-Rabin,sonoprobabilistici,ovvero danno una risposta certa solo se affermano che il numerononè primo, mentre se si ottiene come risultato che il numero è primo, allora c'è solo un'alta probabilità che il numero effettivamente lo sia. I numeri che passano uno di questi test, pur senza essere primi, sono detti "pseudoprimi".La classe più famosa di pseudoprimi è quella deinumeri di Carmichael,che verificano ilpiccolo teorema di Fermatpur essendo composti.

Tra i test di primalità di uso generale il più usato attualmente è l'ECPP,basato sullecurve ellittiche;sebbene la sua complessità computazionale non sia nota, sperimentalmente si osserva che esso è unalgoritmo polinomialenel numero delle cifre din.Nel2002,i tre matematici indiani Manindra Agrawal, Neeraj Kayal e Nitin Saxena hanno sviluppato l'algoritmo AKS,il primo test di primalità deterministico con complessità polinomiale, provando dunque che il problema di stabilire se un numero è primo o no sta nellaclasse di complessitàP.

Algoritmi di fattorizzazione

Un programma che ha lo scopo di individuare i fattori primi di un numero è dettoalgoritmo di fattorizzazione;gli algoritmi di questo tipo possono funzionare anche da test di primalità, ma sono quasi sempre più lenti da eseguire rispetto a programmi ideati solo per quest'ultimo scopo. Dopo il metodo di divisione per tentativi, i più antichi algoritmi di questo tipo sono ilmetodo di Fermat,che si basa sulle differenze tra il numero da fattorizzareNe alcuni quadrati, efficace in particolare quandoNè il prodotto di due numeri primi vicini tra loro, e ilmetodo di Eulero,che si basa invece sulla rappresentazione diNcomesomma di due quadratiin due modi diversi.

Più recentemente, gli algoritmi per la fattorizzazione sono stati basati su una gran varietà di tecniche diverse, come lefrazioni continueo lecurve ellittiche,mentre altri, come ad esempio ilcrivello quadratico,sono basati su miglioramenti del metodo di Fermat. Altri ancora, come ilmetodo rho di Pollard,sono probabilistici, e non offrono la garanzia che, dato un numero non primo, ne trovino i divisori.

A oggi il più veloce algoritmo deterministico di impiego generale, ovvero senza necessità di numeri in forma particolare, è ilgeneral number field sieve,che ha complessità esponenziale sul numero di cifre diN;è stato proposto un algoritmo che ha tempo di esecuzione polinomiale nel numero di cifre diN(algoritmo di Shor), ma esso richiede di essere eseguito su uncomputer quantistico,la cui simulazione su un normale calcolatore richiede un tempo esponenziale.

Impiego nella crittografia

Proprio la difficoltà di fattorizzare grandi numeri ha portato allo sviluppo del primo metodo efficace dicrittografia a chiave pubblica,l'RSA.In questo sistema crittografico, la persona che deve ricevere un messaggio cifrato genera una chiave formata da tre numeri: uno (n) è il prodotto di due numeri primi di grandi dimensioni (generalmente si usano numeri di 1024 o 2048bit), mentre gli altri due (eedf) sono l'uno l'inversodell'altromoduloφ(n) (dove φ indica lafunzione di Eulero). Uno tra questi ultimi due numeri deve essere tenuto segreto (e dunque prende il nome dichiave privata), mentre l'altro deve essere reso noto insieme al numeron(andando a formare la "chiave pubblica" ).

Dopo aver trasformato il messaggio in un numerom(secondo un codice stabilito in precedenza), la procedura di criptazione e decriptazione consiste nell'elevamento a potenza dimper il numero traeedfreso pubblico, prendendone poi il resto nelladivisionepern;ilteorema di Eulerogarantisce che dopo quest'operazione si possa ritornare allo stesso numero di partenza conoscendo siaesiaf.

È possibile, in teoria, ricavare la chiave privata dalle informazioni pubbliche: attualmente questo richiede la fattorizzazione del numeron,rendendo quindi la trasmissione del messaggio sicura se i due primi scelti soddisfano alcune condizioni e sono "sufficientemente" grandi. Non è ancora noto se vi siano metodi efficienti per decriptare il messaggio che non prevedano l'attacco diretto alla fattorizzazione din,ma è stato mostrato che una cattiva scelta della chiave pubblica potrebbe rendere il sistema più vulnerabile ad attacchi di questo tipo.

Nel1991laRSA Security(l'azienda che ha sfruttato commercialmente l'RSA) ha pubblicato una lista disemiprimi,offrendo dei premi in denaro per la fattorizzazione di alcuni di essi, con lo scopo di provare la sicurezza del metodo e di incoraggiare la ricerca in questo ambito: l'iniziativa è stata chiamataRSA Factoring Challenge.Nel corso degli anni, diversi di questi numeri sono stati fattorizzati, mentre per altri il problema è ancora aperto; il concorso si è comunque concluso nel2007.

Numeri primi grandi

Il numero di cifre (inbase 10) del più grande numero primo conosciuto, dal1900al2018.La scala sull'asse delle ordinate è logaritmica.

Già da molti secoli la ricerca di numeri primi "grandi" ha destato l'interesse dei matematici; tuttavia questa ricerca ha assunto una particolare importanza negli ultimi decenni, a causa del bisogno di tali numeri che caratterizza algoritmi quali l'RSA.

Il metodo più efficace per ottenere numeri primi grandi risale al diciassettesimo secolo, quandoMarin Mersennecongetturò che$M_{n}=2^{n}-1$sarebbe stato primo (quandon≤ 257) solo pernuguale a 2, 3, 5, 7, 13, 19, 31, 67, 127 e 257.La verifica della primalità di tali numeri era molto al di sopra delle possibilità dell'epoca, e infatti soltanto nelNovecentosi scoprì che la congettura era falsa e probabilmente fatta "alla cieca", in quanto Mersenne tralasciò tre casi (pern= 61, 89 e 107) e non si accorse che i numeri corrispondenti an= 67 en= 257 erano in realtà composti.

M₁₂₇(un numero di 39 cifre) fu dimostrato essere primo daÉdouard Lucasnel 1876, e rimase il numero primo più grande conosciuto fino al1951,quando vennero trovati (2¹⁴⁸+1)/17 (di 44 cifre) e, poco più tardi, 180 · (2¹²⁷− 1)²+ 1 (di 79 cifre), quest'ultimo tramite un calcolatore elettronico. Da allora tutti i successivi primi più grandi sono stati scoperti con l'aiuto del computer: dal1952(quando loSWACdimostrò cheM₅₂₁è primo) al1996essi sono stati trovati dasupercomputer,e furono tuttiprimi di Mersenne(trovati usando iltest di Lucas-Lehmer,un algoritmo specifico per questi numeri) con l'eccezione di 391581 · 2²¹⁶¹⁹³− 1, che detenne il record tra il1989e il1992.

In seguito, i quattordici nuovi numeri primi più grandi sono stati scoperti attraverso ilGIMPS,un progetto dicalcolo distribuitobasato anch'esso sul test di Lucas-Lehmer. A oggi (dicembre 2018) il più grande numero primo, scoperto nel dicembre del2018,è 2^{82 589 933}− 1, composto da oltre 24 milioni di cifre decimali.I numeri primi noti più grandi sono numeri primi di Mersenne o altri numeri primi particolari, per i quali si dispone di un test molto efficiente in termini computazionali.

LaElectronic Frontier Foundationha offerto dei premi in denaro ai primi che riusciranno a trovare numeri primi di oltre un certo numero di cifre. I primi due di questi premi, di 50 000 e 100 000dollari,sono stati assegnati nel2000e nel2008per il raggiungimento, rispettivamente, di un milione e di dieci milioni di cifre; il più alto premio attualmente in palio è di 250 000 dollari, per l'arrivo al miliardo di cifre.

Generalizzazioni

Rappresentazione dei primi di Gauss di norma minore o uguale a 500. I primi di Gauss sono, per definizione, gli elementi tra gliinteri di Gaussche sono primi.

Il concetto di numero primo viene esteso anche in altri campi della matematica.

Teoria degli anelli

La definizione di numero primo può essere estesa a qualunquedominio d'integrità;vi sono due modi di estendere la definizione, in generale non equivalenti fra loro:

• un elemento èirriducibilese non èinvertibilee non può essere scritto come il prodotto di due elementi anch'essi non invertibili;
• un elemento èprimose non è invertibile e ogni volta che divide il prodottoab,allora divideaoppureb.

Un elemento primo è sempre irriducibile, ma non viceversa: tuttavia nell'anello degliinterile due definizioni sono equivalenti (come garantito dallemma di Euclide), e più in generale sono equivalenti in tutti glianelli a fattorizzazione unica.

Inoltre, dato unanelloA,unidealeIdiAè detto "primo" se per ogni coppiaa,bdi elementi di A tali chea·b∈Ialmeno uno traaebappartiene aI.

Questa definizione è molto vicina a quella degli ordinari numeri primi, tanto che nell'anello$\mathbb {Z}$gliideali priminon nulli sono esattamente (2), (3), (5),..., ovvero quelli generati dai numeri primi (più in generale, ciò avviene in ognidominio ad ideali principali). Lo studio degli ideali primi è un punto centrale nellageometria algebricae nellateoria algebrica dei numeri.Un'importante analogia tra numeri primi e ideali primi è dato dal fatto che neidomini di Dedekindper gli ideali vale l'analogo delteorema fondamentale dell'aritmetica.

Teoria dei gruppi

Nellateoria dei gruppi,un ruolo simile a quello dei numeri primi è rivestito daigruppi semplici.Si può dimostrare infatti che ogni gruppo finitoGammette unaserie di composizione,cioè una serie del tipo

$1=H_{0}\triangleleft H_{1}\triangleleft \cdots \triangleleft H_{m}=G,$

ove ogniH_iè unsottogruppo normalediH_i+1tale che il gruppoH_i+1/H_i(detto gruppo fattore della serie) sia un gruppo semplice. Ilteorema di Jordan-Hölderassicura che tutte le serie di composizione perGhanno la stessa lunghezzame gli stessi fattori di composizione, a meno dipermutazionieisomorfismi.È tuttavia da notare che gruppi diversi possono avere la stessa serie di composizione: ad esempio ilgruppo ciclico$\mathbb {Z} _{2p}$e ilgruppo diedraleD_p,per ogni primop,hanno entrambi la serie di composizione

$1\triangleleft \mathbb {Z} _{p}\triangleleft G,$

corrispondente ai fattori$\mathbb {Z} _{2}$e$\mathbb {Z} _{p}$.

Teoria dei nodi

Alcuni nodi primi

Inteoria dei nodi,unnodo primoè unnodonon banale che non può essere "scomposto" in due nodi più piccoli. In maniera più precisa, è un nodo che non può essere scritto comesomma connessadi due nodi non banali.

Nel1949Horst Schubertdimostrò un teorema di fattorizzazione analogo al teorema fondamentale dell'aritmetica, che asserisce che ogni nodo è ottenibile in modo unico come somma connessa di alcuni nodi primi.Per questo motivo, i nodi primi hanno un ruolo centrale nella teoria dei nodi: una loro classificazione è stato da sempre il tema centrale della teoria fin dalla fine delXIX secolo.

Numeri primi in natura

UnaMagicicadacon periodo di 17 anni

In natura compaiono molti numeri, ed è quindi inevitabile che alcuni di essi siano primi. Sono tuttavia relativamente pochi gli esempi di numeri la cui presenza in natura si spieghi con la loro primalità.

Per la maggior parte, lestelle marinehanno 5 braccia, e 5 è un numero primo; tuttavia non è nota alcuna connessione tra questo numero di braccia e la primalità di 5.Il motivo della simmetria a 5 braccia che caratterizza la maggior parte delle stelle marine e molti altriechinodermirimane un mistero.

Inentomologiasi trova uno dei casi in cui si suppone che un numero compaia proprio in quanto primo. Si è infatti notato che alcune specie dicicaledel genereMagicicada,che trascorrono la maggior parte delle loro vite comelarve,emergono come pupe solo a intervalli di 13 o 17 anni, dopo di che si riproducono e infine muoiono dopo poche settimane. Si pensa che il motivo per cui l'intervallo di tempo è un numero primo di anni sia la difficoltà per un predatore di evolversi specializzandosi nella predazione delleMagicicada:se infatti questi insetti apparissero dopo un numero non primo di anni, allora tutti i predatori il cui ciclo vitale fosse un divisore di quel numero avrebbero una elevata probabilità di trovare leMagicicada.Sebbene esile, questo vantaggio evolutivo sembra essere stato sufficiente a selezionare cicale il cui periodo è di 13 o 17 anni.

Numeri primi nell'arte e nella letteratura

I numeri primi hanno influenzato molti artisti e scrittori. Il compositore franceseOlivier Messiaenera ossessionato da tali numerie li utilizzò per creare musica non metrica: in opere comeLa Nativité du Seigneur(1935) oQuatre études de rythme(1949-50) impiegò simultaneamente motivi la cui lunghezza è un numero primo per creare ritmi imprevedibili. Secondo Messiaen questo modo di comporre era "ispirato dai movimenti dalla natura, movimenti di durate libere e disuguali".Anche nel movimento di apertura di un'altra composizione,Quatuor pour la fin du temps,Messiaen utilizzò i numeri primi. Con l'obiettivo di dare l'idea dell'eternità, accostò infatti un tema di 17 note a un tema di 29 note. Essendo primi entrambi i numeri, i temi si ripetono insieme solo dopo 17 · 29 = 493 note. La stessa idea è stata utilizzata daJem Finerche ha ideato un'installazione sonora che sino al 31 dicembre 2999 suonerà motivi sempre diversi.

I numeri primi svolgono un ruolo anche in alcuni libri. Ad esempio, nel romanzo di fantascienzaContactdiCarl Sagan(così come nella suaversione cinematografica), i numeri primi vengono utilizzati dagli alieni per comunicare; un caso reale di uso dei primi come mezzo di comunicazione è presente nel saggioL'uomo che scambiò sua moglie per un cappello,del neurologoOliver Sacks,dove sono descritti due gemelliautisticiche per parlarsi si scambiano primi molto elevati. Vi sono riferimenti ai numeri primi anche nel romanzo diMark HaddonLo strano caso del cane ucciso a mezzanotte,in cui la numerazione dei capitoli segue la successione dei primi, e nel romanzo diPaolo GiordanoLa solitudine dei numeri primi,vincitore delpremio Streganel 2008. Il romanzoLo zio Petros e la congettura di GoldbachdiApostolos Doxiadis(pubblicato in italiano nel 2001) è stato trasposto per le scene daAngelo Savelli.

Molti film riflettono la fascinazione popolare verso i misteri dei numeri primi e della crittografia, come ad esempioCube - Il cubo,I signori della truffa,L'amore ha due facce,A Beautiful MindeLa solitudine dei numeri primi.

Note

Annotazioni

Fonti

Bibliografia

• (EN)Tom M. Apostol,Introduction to Analytic Number Theory,2ª ed., New York, Springer-Verlag, 1976,ISBN0-387-90163-9.
• Michael Artin,Algebra,Torino, Bollati Boringhieri, 1997,ISBN88-339-5586-9.
• Carl B. Boyer,Storia della matematica,Milano, Mondadori, 1990,ISBN978-88-04-33431-6.
• John H. ConwayeRichard K. Guy,Il libro dei numeri,Milano, Hoepli, 1999,ISBN88-203-2519-5.
• Harold Davenport,Aritmetica superiore,Bologna, Zanichelli, 1994,ISBN88-08-09154-6.
• Keith Devlin,Dove va la matematica,Torino, Bollati Boringhieri, 1994,ISBN88-339-1182-9.
• Marcus du Sautoy,L'enigma dei numeri primi,Milano, Rizzoli, 2004,ISBN88-17-00843-5.
• Euclide,Elementi
• (EN) Richard K. Guy,Unsolved problems in number theory,3ª ed., New York, Springer-Verlag, 2004,ISBN0-387-20860-7.
• (EN)Godfrey Harold HardyeEdward M. Wright,An Introduction to the Theory of Numbers,6ª ed., Oxford, Oxford University Press, 2008,ISBN978-0-19-921986-5.
• (EN)Albert Edward Ingham,The Distribution of Prime Numbers,Cambridge, Cambridge University Press, 1932,ISBN0-521-39789-8.
• (EN) 2004 Leo Moser,An Introduction to the Theory of Numbers,West Lafayette (Indiana, USA), The Trillia Group,ISBN978-1-931705-01-1.URL consultato il 1º settembre 2009.
• Giulia Maria Piacentini Cattaneo,Algebra - un approccio algoritmico,Padova, Decibel-Zanichelli, 1996,ISBN978-88-08-16270-0.
• Simon Singh,Codici & segreti,Milano, Rizzoli, 1999,ISBN88-17-86213-4.
• (EN)Ian Stewarte David Tall,Algebraic number theory and Fermat's last theorem,3ª ed., Natick, Massachusetts, A K Peters, 2002,ISBN1-56881-119-5.
• (EN)Terence Taoe Van Vu,Additive combinatorics,Cambridge, Cambridge University Press, 2006,ISBN978-0-521-85386-6.
• (EN) Song Y. Yan,Primality testing and integer factorization in public-key cryptography,Boston, Kluwer Academic Publishers, 2004,ISBN1-4020-7649-5.

Voci correlate

Principali teoremi e congetture sui numeri primi

• Congettura dei numeri primi gemelli
• Congettura di Legendre
• Congettura di Goldbach
• Congettura di Opperman
• Ipotesi di Riemann
• Reciprocità quadratica
• Piccolo teorema di Fermat
• Postulato di Bertrand
• Teorema di Fermat sulle somme di due quadrati
• Teorema dei numeri primi
• Teorema dell'infinità dei numeri primi
• Teorema di Mills
• Teorema di Wilson
• Test di Fermat
• Test di Lucas-Lehmer
• Test di Miller-Rabin

Numeri primi

• Lista di numeri primi
• Numero omirp
• Numeri primi cugini
• Numero primo di Eisenstein
• Numero di Belfagor
• Numero di Fermat
• Numero primo di Mersenne
• Numero primo di Sophie Germain
• Numero primo troncabile
• Numeri primi gemelli
• Numero primo illegale
• Numeri primi sexy
• Primo palindromo
• Primo circolare
• Primo cubano
• Repunit#Primi repunit

Altre

• Costante di Copeland-Erdős
• Criteri di divisibilità
• Crivello di Eratostene
• Funzione enumerativa dei primi
• Il più grande numero primo conosciuto
• Intero gaussiano
• Ipotesi di Riemann
• Spirale di Ulam
• Numero pratico

Altri progetti

Altri progetti

• Wikiquote
• Wikizionario
• Wikimedia Commons

• Wikiquotecontiene citazioni suinumero primo
• Wikizionariocontiene il lemma di dizionario «numero primo»
• Wikimedia Commonscontiene immagini o altri file sunumero primo

• Wikinotiziecontiene l'articoloScoperti i due nuovi numeri primi più grandi a distanza di pochi giorni,18 settembre 2008

• Wikinotiziecontiene l'articoloIntervista a Marcus du Sautoy,4 ottobre 2007

Collegamenti esterni

• primo,susapere.it,De Agostini.
• numero primo,inEnciclopedia della Matematica,Istituto dell'Enciclopedia Italiana,2013.
• (EN)prime,suEnciclopedia Britannica,Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein,Prime Number,suMathWorld,Wolfram Research.
• (EN)Prime number,suEncyclopaedia of Mathematics,Springer e European Mathematical Society.
• (EN) Chris Caldwell,The Prime Pages,suutm.edu.URL consultato l'11 settembre 2009(archiviato dall'url originaleil 1º agosto 2003).
• Laura Listanti,Il mistero dei numeri primi e la sicurezza informatica(PDF), suulisse.sissa.it.URL consultato l'11 settembre 2009(archiviato dall'url originaleil 22 luglio 2011).
• (EN)Fast Online primality test with factorization,sualpertron.com.ar.URL consultato il 28 aprile 2014.java aplet che implementa ilMetodo delle curve ellittiche,capace di testare la primalità di numeri con migliaia di cifre.
• (EN) Paolo Ardoino,Random prime numbers using OpenSSL bignum,suardoino.com.URL consultato l'11 settembre 2009(archiviato dall'url originaleil 20 dicembre 2009).
• (EN) Mark Chamness,Prime number generator,sualumnus.caltech.edu.URL consultato l'11 settembre 2009(archiviato dall'url originaleil 4 settembre 2009).