Angolo

Unangolo(dallatinoangulus,dalgrecoἀγκύλος (ankýlos), derivazione dalla radiceindoeuropeaank,piegare, curvare[1]), inmatematica,indica ciascuna delle due porzioni dipianocomprese tra duesemiretteaventi la stessa origine. Si può definire ancheangolo pianoper distinguerlo dal concetto derivato diangolo solido.Le semirette vengono dette lati dell'angolo, e la loro origine vertice dell'angolo. Il termine, così definito, riguarda nozioni di larghissimo uso, innanzitutto nellageometriae nellatrigonometria.
A ogni angolo si associa un'ampiezza, la misura correlata alla posizione di una semiretta rispetto all'altra e pertanto alla conformazione della porzione di piano costituente l'angolo: essa si esprime in gradisessagesimali,in gradisessadecimali,ingradi centesimalio inradianti,sempre con valorireali.[2]
Associando all'angolo un verso si introducono le ampiezze degli angoli con segno, che consentono di definirefunzioni trigonometrichecon argomenti reali anche negativi. Le ampiezze con segno forniscono contributi essenziali alle possibilità delcalcolo infinitesimalee alle applicazioni allafisica classicae alle conseguenti discipline quantitative.
Angolo convesso e concavo
[modifica|modifica wikitesto]
Si chiama angolo concavo l'angolo che contiene i prolungamenti delle semirette (lati) che lo formano. L'angolo convesso è la porzione di piano che non contiene i prolungamenti delle semirette che dividono il piano. Gli angoli convessi hanno ampiezza compresa tra 0 e 180 gradi sessagesimali, da 0 a 200 gradi centesimali, da 0 aradianti; mentre l'ampiezza degli angoli concavi misura tra 180 e 360 gradi, da 200 a 400 gradi centesimali, daaradianti. Le ampiezze sono sempre non negative.
Se le semirette sono diverse, ma appartengono alla stessa rettaciascuno dei due semipiani definiti damuniti del vertice (che distingue le semirette) si diceangolo piatto.
A parte il caso particolare dell'angolo piatto, il piano si tripartisce in tre insiemi: lafrontiera dell'angolo,ossia l'insieme dei punti appartenenti alle due semiretteetra cui il vertice, e dueinsiemi connessiee separati dai punti della frontiera. Di questi due insiemi, soloè costituito da punti che appartengono a segmenti con un estremo su una semiretta e l'altro sull'altra; in altre parole soloè uninsieme convesso.Il terzo insiemenon è convesso. Si definisceangolo convessodeterminato dael'unione di questo insieme convesso e della frontiera,.Si definisceangolo concavodeterminato dael'unione del terzo insieme non convesso e della frontiera,.I due angoli definiti dalle due semirette si diconoangoli esplementari.
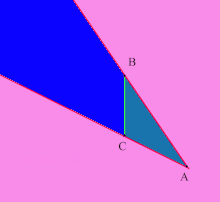
Angoli convessi e concavi sono sottoinsiemiillimitatidel piano, quindi sono insiemi non misurabili attraverso la loroareache ha valore infinito. Spesso con angolo (convesso) si indica anche la parte di piano delimitata da due segmenti con un estremo in comune (vertice). Si può ricondurre questa definizione alla precedente prolungando i due segmenti dalla parte del loro estremo diverso dal vertice per ottenere le due semirette. Questa estensione della definizione rende lecito assegnare a ogni triangolo tre angoli (convessi) associati biunivocamente ai suoi tre vertici.
Tuttavia il triangolo, essendo un sottoinsieme chiuso e limitato del piano, ha area finita, infatti esso è l'intersezione degli angoli corrispondenti ai suoi tre vertici.
La misurazione dell'ampiezza degli angoli convessi e concavi
[modifica|modifica wikitesto]Considerazioni preliminari
[modifica|modifica wikitesto]È naturale porsi il problema di "misurare un angolo": gli angoli possono servire per tante costruzioni e se a essi si associano misure numeriche ci si aspetta che per molte costruzioni possano essere utili calcoli numerici su queste misure.
Il problema della misura di un angolo non può essere risolto attraverso una misura della sua superficie che non èlimitatae che comunque non sarebbe significativa nemmeno nel caso di angoli sottesi da segmenti come nel caso del triangolo: si considerino per esempio triangoli simili.
Se si hanno due angoli convessi o concaviecon lo stesso vertice eè sottoinsieme di(situazione che si determina solo se i lati disono sottoinsiemi di) è ragionevole chiedere che la misura disia maggiore della misura di.
Dato un angolo convessosi dicesemiretta bisettricedell'angolo la semiretta avente il vertice dicome estremo e i cui punti sono equidistanti dai lati di.Si può costruire facilmente labisettricecon un compasso. La semiretta bisettrice di un angolo concavo si definisce come la semiretta avente come estremo il vertice dell'angolo allineata con la bisettrice del suo angolo (convesso) esplementare.
La semiretta bisettricedi un angoloconvesso o concavo e ciascuno dei suoi due lati determinano due angoli convessi. La riflessione rispetto alla retta contenente lascambia i due lati die trasforma uno dei due angoli nell'altro. È quindi ragionevole attribuire ai due angoli determinati dalla bisettrice una misura che sia la metà della misura di.È altrettanto ragionevole considerare che le misure dei due angoli determinati dalla semiretta bisettrice siano la metà della misura dell'angolo di partenza. Il processo di dimezzamento di un angolo può essere ripetutovolte congrande a piacere.
Un angolo convesso si diceangolo rettose i suoi due lati sono ortogonali, cioè unangolo rettoè la metà di un angolo piatto.
Un angolo convesso contenuto in un angolo retto avente il suo stesso vertice si diceangolo acuto.Un angolo convesso contenente un angolo retto avente lo stesso vertice si diceangolo ottuso.
Due angolieche hanno in comune solo una semiretta e non hanno alcun punto interno in comune si diconoangoli consecutivi.Se due angoli consecutivi hanno le semirette non in comune opposte (cioè la loro unione è una retta) allora si diconoangoli adiacenti.Per quanto riguarda gli angoli consecutivi, se questi sono angoli convessi la loro unione è un angolo che potrebbe essere convesso o concavo: si tratta dell'angolo definito dalle due semirette che sono i lati di uno solo dei due angoli. A questo angolo unione è ragionevole assegnare come misura la somma delle misure degli angoli consecutivi. L'angolo unione si dice "somma" dei due angolie.
In base alle considerazioni precedenti è lecito attribuire agli angoli misure costituite da numeri reali.
Due angoli trasformabili l'uno nell'altro medianteisometriesi dicono congruenti. Evidentemente una misura degli angoli invariante per le isometrie costituisce uno strumento con molti vantaggi: in particolare consente di individuare le classi di congruenza degli angoli. Quindi si chiede una misura degli angoli a valori reali e invariante per congruenza.
Dalla misura dell'angolo alla misura dell'ampiezza dell'angolo
[modifica|modifica wikitesto]Se l'angolo è definito come la porzione del piano tra due semirette, la sua unità di misura dovrebbe essere una lunghezza al quadrato, ma questa misura non ha né significato né utilità pratica. Si è quindi pensato di considerare non la misura dell'angolo in sé, ma quella dell'ampiezzadel movimentoche porta una delle semirette a sovrapporsi all'altra.
Come giungere a determinare l'ampiezza di un angolo ha certamente chiesto maggiori sforzi all'intelletto umano di quanti ne abbia richiesti la misurazione di lunghezze e superfici.Misuraresignifica esprimere unagrandezzain rapporto a un'altra grandezza data, a essa omogenea, che funge daunità di misura.Se questo processo sorge abbastanza spontaneo per le grandezze spaziali, per cui basta ripetere un segmento o affiancare un quadratopervolte fino all'esaurimento della lunghezza o della superficie (), lo stesso diventa meno intuitivo per le grandezze angolari, dove pure la stessa elaborazione mentale di un'unità di misura adatta richiede un maggior grado di astrazione.

Si prendano in considerazione i quattro angoli di ampiezzadella figura. Volendoli quantificare con l'area delimitata dai lati in verde, prolungando i lati a infinito nel casosi ottiene un'area infinita e nei restanti casieconsiderando solo le superfici entro le linee tratteggiate, tre aree determinate e quindi misurabili, ma visibilmente diverse fra loro, seppur originate dal medesimo angolo. Si presuma inoltre di dividereesattamente in due angoli uguali, in modo che sia esprimibile in rapporto a questi ultimi, come,.Per quanto detto sopra,può quindi essere considerato un'unità di misurae, se ora se ne considera l'area, l'uguaglianza sarà soddisfatta soltanto dai casiema non dadove i due triangoli hanno aree diverse, pur trattandosi di due angoliperfettamente sovrapponibili. Ne discende che l'angolo non può essere misurato idoneamente in termini diarea.
Si immagini quindi una semiretta che partendo dalla posizione verticale giri attorno al proprio estremo fino a diventare orizzontale; la semiretta ha compiuto un angoloe nel suo movimento ha coperto la superficie compresa tra le due semirette. Sovrapponendo idealmente le immaginiesi nota che, come in uncompasso,allontanandosi dal centro di rotazione ogni punto traccia sul piano unarcopiù lungo, pur mantenendo immutato il rapporto fra lunghezza di quest'ultimo e il raggio. Inoltre se la semiretta compisse soltanto l'angolola lunghezza degli archi prodotti sarebbe invariabilmente la metà della lunghezza degli archi loro omologhi in.
Si consideri ora una rotazione completa che riporta la semiretta alla posizione di partenza, cioè un angolo di massima ampiezza. In questo caso la semiretta copre l'intera superficie del piano tracciando infinite circonferenze; prendendo una qualunque di queste e segmentandola inparti uguali, si possono individuare per ogni arco altrettante porzioni di piano equipollenti, in pratica una generica unità di misura per l'angolo. Dunque soltanto capendo che la misurazione dell'angolo non può essere avvenire quantificando un'area si comprende che bisogna astrarre il concetto di angolo come parte del piano e considerarlo invece cinematicamente come una porzione di superficie coperta da una semiretta in rotazione sul proprio estremo. Solo in questo modo è possibile misurarlo.
Sebbene questa nozione non sia immediata, deve comunque trattarsi di una conquista concettuale antica, se il sistema per la misurazione degli angoli comunemente più utilizzato ancora oggi, ilsistema sessagesimale,è giunto sino noi dall'anticaciviltà babiloneseinvariato nei secoli.[3]
Sistemi di misurazione dell'ampiezza dell'angolo
[modifica|modifica wikitesto]Nel sistema sessagesimale l'angolo completo oangolo giroè suddiviso in 360 spicchi, equivalenti all'unità di misura convenzionale denominatagrado sessagesimale,indicata col simbolo°.La ragione della divisione in 360 parti dell'angolo giro è riconducibile all'usoastronomicoche i babilonesi facevano di questa misura[3]:dato che il Sole compie un giro completo sulla volta celeste nell'arco di un anno, a quel tempo stimato di circa 360 giorni, un grado corrisponde pressappoco allo spostamento del Sole sull'eclitticain un giorno.
Il nome "grado sessagesimale" deriva dal fatto che le sottounità del grado, ilminutoe ilsecondo,sono divise in sessantesimi; perciò, come nell'orologio, ogni grado è diviso in 60 minuti primi indicati col simbolo'e chiamati semplicemente minuti, e ogni minuto è diviso in 60 minuti secondi indicati col simbolo''e chiamati semplicemente secondi. Ulteriori suddivisioni del secondo seguono invece il comune sistema decimale. Questa suddivisione deriva dal fatto che nell'antica Babilonia era in auge unsistema numericosu basesessagesimale,giunto sino a noi quale retaggio storico nell'orologio e suigoniometri.
L'ampiezza di un angolo potrebbe quindi essere espresso in una forma tipo:
Nel tempo sono poi stati adottati altri sistemi di misurazione nel tentativo di rendere più agevole la misura dell'ampiezza dell'angolo. Alla fine del Settecento non sfuggì ai tentativi di razionalizzazione neppure il sistema sessagesimale: venne proposto unsistema centesimale,basato appunto sulgrado centesimalequale centesima parte nell'angolo retto, eletto ad angolo fondamentale per sostituire il 90 col più tondo e comodo 100, anche se trovò utilizzo pratico soltanto attorno al 1850 quandoIgnazio Porro[4]lo usò per costruire i suoi primi strumenti a divisione centesimale. Con questo sistema l'angolo giro viene diviso in 400 spicchi uguali con sottomultipli a frazioni decimali. Si tratta ancora di una unita di misura convenzionale non motivata da alcuna ragione matematica.
Dallo sviluppo dell'analisi infinitesimale guadagnò sempre più importanza un'altra unita di misura, per certi aspetti più "motivata" o "naturale": ilradiante,inteso come rapporto tra la lunghezza di unarcodicirconferenzae il raggio della circonferenza stessa in quanto questo rapporto non dipende dal raggio, ma solo dall'angolo compreso. In questo modo l'angolo giro misura 2π,cioè il rapporto tra la lunghezza della circonferenza e il suo raggio.
Riepilogando, per misurare l'ampiezza dell'angolo i sistemi di misura più attestati sono[2]:
- ilsistema centesimale,con unità di misura ilgrado centesimale;
- ilsistema sessagesimale,con unità di misura ilgrado sessagesimale;
- ilsistema sessadecimale,con unità di misura ilgrado sessadecimale.È una variante del precedente con divisione dell'angolo giroin 360 parti in cui i sottomultipli dei gradi sono espressi in forma decimale;
- ilsistema radiante,osistema matematico,con unità di misura ilradiante.
- in ambito militare si usa anche ilmillesimo di radiante,detto comunemente "millesimo", che viene impiegato per determinare gli scarti e relative correzioni nei tiri con l'artiglieria. Su una circonferenza avente raggio un km equivale a una corda lunga un metro. Per esempio, per correggere un colpo caduto 100 metri a destra di un bersaglio posto alla distanza di 10 km bisognerà apportare una correzione di 10°° (millesimi) rosso. La scala graduata che si osserva all'interno di alcuni binocoli è espressa in millesimi di radianti, il colore rosso significa rotazione verso sinistra mentre il colore verde significa rotazione verso destra.
Il primo viene più che altro usato in ambito strettamentetopografico,mentre gli ultimi sono quelli maggiormente usati, il secondo per consuetudine il terzo per una maggiore semplicità dei calcoli nelle formule matematiche. La relazione che lega il sistema radiante e il sistema sessagesimale e permette il passaggio da uno all'altro è
doveè la misura dell'ampiezza dell'angolo espresso in gradi eè la misura espressa in radianti.
Conversioni angolari
[modifica|modifica wikitesto]Indicando l'ampiezza di un angolo con:
- nelsistema sessagesimale,dovesono rispettivamente i gradi, primi e secondi d'arco (numeri interi)
- nelsistema sessadecimale
- nelsistema centesimale
- nelsistema matematico,
indicando conlaparte interadi un numero reale e ricordando che vale la proporzione generale
valgono le seguenti formule di conversione da un sistema di misura all'altro
| Conversione daa | Sessagesimale | Sessadecimale | Centesimale | Matematico |
|---|---|---|---|---|
| Sessagesimale | doveè calcolato con la formula precedente | doveè calcolato con la formula precedente | ||
| Sessadecimale |
|
|||
| Centesimale | quindi si applicano le formule precedenti per la conversione da sessadecimale a sessagesimale |
|||
| Matematico | quindi si applicano le formule precedenti per la conversione da sessadecimale a sessagesimale |
Ampiezze di angoli particolari
[modifica|modifica wikitesto]
- Unangolo acutoha ampiezza inferiore a quella di un angolo retto, ossia
- Unangolo rettoha l'ampiezza uguale a un quarto dell'ampiezza di un angolo giro, ossia
- Unangolo ottusoha l'ampiezza compresa fra quelle di un angolo retto e di un angolo piatto, ossia
- Unangolo piattoha ampiezza pari a metà di quella di un angolo giro, ossia
- Unangolo giroha ampiezza uguale a
- e corrisponde a una rotazione completa di una semiretta intorno al suo estremo.
- Unangolo concavoha ampiezza maggiore di quella di un angolo piatto,
- Unangolo convessoha ampiezza minore di quella di un angolo piatto,
Angoli complementari
[modifica|modifica wikitesto]Nella nomenclatura degli angoli di ampiezza compresa tra 0 esi è soliti usare aggettivi particolari per gli angoli associati a un angolo dato in quanto suoi "angoli di complemento" rispetto agli angoli fondamentali retto, piatto e giro.
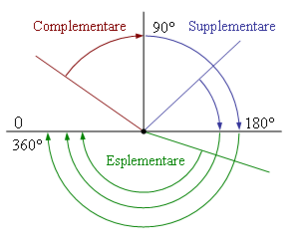
Si dicecomplementaredi un angolo di ampiezzaogni angolo avente come ampiezza la"mancante" per ottenere un angolo retto, cioè tale che sia.Da questa definizione segue che due angoli complementari devono essere entrambi acuti e che ha senso attribuire un complementare solo a unangolo acuto.
Si dicesupplementaredi un angolo di ampiezzaogni angolo avente come ampiezza la"mancante" per ottenere un angolo piatto, cioè tale che sia.Da questa definizione segue che ogni supplementare di un angolo acuto è unangolo ottusoe viceversa, mentre ogni supplementare di un angolo retto è anch'esso un angolo retto. Quando due angoli supplementari sono ancheconsecutivi,cioè hanno in comune solo una semiretta, vengono detti anche angoliadiacenti.
Si diceesplementaredi un angolo di ampiezzaogni angolo avente come ampiezza la"mancante" per ottenere un angolo giro, cioè tale che sia.Ne segue che ogni esplementare di un angolo concavo è un angolo convesso e viceversa, mentre ogni esplementare di un angolo piatto è anch'esso piatto.
Angoli opposti al vertice
[modifica|modifica wikitesto]
Dueretteche si intersecano dividono il piano in quattro angoli; considerato uno qualsiasi di questi angoli: due degli altri gli sono adiacenti mentre il terzo, con cui condivide solo il vertice, è dettoangolo opposto al vertice.Due angoli sono tra loro opposti al vertice se i prolungamenti dei lati di uno risultano essere i lati dell'altro.
Due angoli opposti al vertice sono sempre congruenti.
Dimostrazione
Per definizione, due angoli adiacenti equivalgono a un angolo piatto, per cui valgono le seguenti uguaglianze
da cui
- cvd.
Sono adiacenti gli angoli delle coppie(α, β),(β, γ),(γ, δ)e(α, δ).
Sono invece opposti al vertice gli angoli delle coppie(α, γ)e(β, δ).
Angoli formati da rette tagliate da una trasversale
[modifica|modifica wikitesto]Quando sul piano due rette distinteevengono tagliate da un trasversale(incidente sia ache a), si originano otto angoli ognuno dei quali è posto in relazione con quelli che non hanno lo stesso vertice.

Con riferimento ai due semipiani separati dalla trasversalesono definiticoniugatidue angoli con vertici distinti disposti sullo stessosemipiano.Rispetto alle retteeinvece, sono definitiesternidue angoli con vertici distinti che non intersecano la retta su cui giace un lato dell'altro angolo, mentre sono consideratiinternidue angoli con vertici distinti che intersecano la retta su cui giace un lato dell'altro angolo. Sono inoltre definiticorrispondentidue angoli coniugati tali che un lato di uno dei due angoli è contenuto in un lato dell'altro angolo. Con riferimento alla figura si ha la seguente esemplificazione.
- Sono corrispondenti le coppie:
- Sono coniugati interni le coppie:
- Sono coniugati esterni le coppie:
- Sono alterni interni le coppie:
- Sono alterni esterni le coppie:
Nel caso in cui le due retteesianoparallelegli angoli corrispondenti e gli angoli alterni, dello stesso tipo, sono congruenti. Invece gli angoli coniugati, anch'essi dello stesso tipo, sonosupplementari.
Somma degli angoli interni
[modifica|modifica wikitesto]Nellageometria euclideala somma degli angoli interni di un triangolo è sempre di 180 gradi. Più in generale, data una qualunque figura geometrica convessa dilati, la somma di tutti i suoi angoli interni è uguale agradi. Quindi, per esempio, la somma totale di tutti gli angoli interni di un quadrilatero è uguale agradi. Un caso particolare è dato dal quadrato, che ha quattro angoli retti, la cui somma è infatti 360 gradi. Analogamente, la somma di tutti gli angoli interni di un pentagono, regolare o meno, è uguale a 540 gradi.
In altregeometrie,dettenon euclidee,la somma degli angoli interni di un triangolo può assumere sia valori maggiori sia valori minori di 180 gradi.
Angoli con segno
[modifica|modifica wikitesto]Molti problemi portano ad ampliare la nozione di angolo in modo da disporre di un'entità a cui si possa attribuire un'ampiezza data da un numero reale e quindi anche superiore a 360 gradi e negativa. Per questo occorre abbandonare l'associazione angolo - sottoinsieme del piano. Si dice che un angoloè maggiore di un angoloquando una parte di angoloè congruente all'angolo.Un angolo convesso o concavo può essere descritto cinematicamente come la parte di piano "spazzata" da una semiretta mobile che ruota mantenendo fisso il suo estremo; questo è il vertice dell'angolo e le posizioni iniziale e finale della semiretta sono i lati dell'angolo. Questa descrizione porta a distinguere due versi del movimento rotatorio. Si definisceverso negativooverso orarioil verso della rotazione che, osservata dal di sopra del piano, corrisponde al movimento delle lancette di un orologio tradizionale; si definisceverso positivooverso antiorarioil verso opposto (ad esempio).
Per sviluppare considerazioni quantitative si considera una circonferenzail cui centro ha il ruolo del verticeper gli angoli che si prendono in considerazione. Il raggiodi questa circonferenza può essere scelto ad arbitrio e talora risulta comodo avere;quando si riferisce il piano a una coppia di assi cartesiani risulta comodo porre il vertice degli angoli nell'origine, in modo che la circonferenza corrisponda all'equazione.
Ogni angolo di verticedetermina un arco sulla circonferenza. Si consideri ora un movimento di una semiretta con estremo inin un verso o nell'altro da una posizione inizialefino a una posizione finale:esso determina sullaunarco orientatoche ha come estremo iniziale il punto in cuiviene intersecata dallae come estremo finale il punto in cui viene intersecato dalla.Si può pensare l'arco orientato come se fosse "tracciato" dalla penna di un compasso avente l'altro braccio nel puntoGli archi orientati con verso positivo si possono chiamare semplicemente archi (di circonferenza) positivi, quelli con verso negativo archi negativi.
Si può estendere la nozione di arco orientato pensando che il compasso possa compiere più di un giro, in verso positivo o negativo.
Si possono identificare gli angoli convessi con gli angoli relativi agli archi positivi interamente contenuti in una semicirconferenza; gli angoli concavi con gli archi positivi che contengono una semicirconferenza e sono contenuti in una circonferenza.
A questo punto si possono definire comeangoli con segnodi verticele entità che generalizzano gli angoli convessi e concavi con vertice ine sono associate biunivocamente agli archi orientati sulla circonferenza.
Gli angoli con segno possono essere sommati senza le restrizioni degli angoli associati a parti di piano e gli archi relativi risultano essere giustapposti; angolo opposto a un angolo dato corrisponde all'arco considerato con il verso opposto. Di conseguenza agli angoli con segno si attribuisce un'ampiezza rappresentata da un numero reale tale che alla somma di due angoli con segno corrisponda lasomma algebricadelle ampiezze.
A questo punto si è indotti naturalmente ad associare all'ampiezza di un angolo con segno la lunghezza con segno del corrispondente arco. Questo richiede di precisare cosa si intenda perlunghezza di un arcoe più in particolare richiede di definire la lunghezza di una circonferenza
Le considerazioni sulla rettificazione di una circonferenza portano alla definizione del numeroe, sul piano computazionale, alle valutazioni del suo valore.
Angoli solidi
[modifica|modifica wikitesto]Un angolo solido è un'estensione allospazio tridimensionaledel concetto di angolo.
Note
[modifica|modifica wikitesto]- ^Jonathan Slocum,Indo-European Lexicon: PIE Etymon and IE Reflexes,suutexas.edu,Linguistics Research Center, University of Texas, Austin, 4 marzo 2010.URL consultato il 28 maggio 2024(archiviato dall'url originaleil 27 giugno 2010).
- ^abAngular Unit,suThe Free Dictionary.
- ^abCarl B. Boyer e Uta C. Merzbach,A History of Mathematics,Terza Edizione, pp. 21-36.
- ^Strumenti navali(archiviato dall'url originaleil 9 giugno 2006).
Voci correlate
[modifica|modifica wikitesto]Altri progetti
[modifica|modifica wikitesto] Wikizionariocontiene il lemma di dizionario «angolo»
Wikizionariocontiene il lemma di dizionario «angolo» Wikimedia Commonscontiene immagini o altri file sull'angolo
Wikimedia Commonscontiene immagini o altri file sull'angolo
Collegamenti esterni
[modifica|modifica wikitesto]- Angolo,suTreccani.it – Enciclopedie on line,Istituto dell'Enciclopedia Italiana.
- Raffaello NICCOLI, Federigo ENRIQUES e Luigi Volta,ANGOLO,inEnciclopedia Italiana,Istituto dell'Enciclopedia Italiana,1929.
- Àngolo,suVocabolario Treccani,Istituto dell'Enciclopedia Italiana.
- Angolo,suVocabolario Treccani,Thesaurus,Istituto dell'Enciclopedia Italiana,2018.
- àngolo (geometria),susapere.it,De Agostini.
- Angolo,inEnciclopedia della Matematica,Istituto dell'Enciclopedia Italiana,2013.
- (EN)angle,suEnciclopedia Britannica,Encyclopædia Britannica, Inc.
- (EN) Eric W. Weisstein,Angle,suMathWorld,Wolfram Research.
- (EN)Angle,suEncyclopaedia of Mathematics,Springer e European Mathematical Society.
- (EN)IUPAC Gold Book, "angle",sugoldbook.iupac.org.
| Controllo di autorità | Thesaurus BNCF30974·LCCN(EN)sh85005042·GND(DE)4189964-7·BNF(FR)cb14519948f(data)·J9U(EN,HE)987007294852305171 |
|---|

































![{\displaystyle Int[\;]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7f270d340d149cf4f9a14573f6ac8b700c7921b)






![{\displaystyle \alpha =Int[\alpha ^{\circ }]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abef4f85232d5f4206c193fa6ffa4a3564830493)
![{\displaystyle p=Int[(\alpha ^{\circ }-\alpha )\cdot 60]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e751c169c8a18b4f6e159a49af9856605c3f07a)




































