하이퍼 연산

수학에서하이퍼 연산 수열(Hyperoperation sequence)은하이퍼 연산이라 불리는덧셈,곱셈,거듭제곱으로 시작하는이항연산 수열이다. 이 수열의n번째 하이퍼 연산은n의 그리스어 접두사에 접미사-ation을 붙인 단어로 불리며,커누스 윗화살표 표기법에서 (n-2)개의 화살표로 표기할 수 있다.

정의

하이퍼 연산 수열은 덧셈 (n = 1), 곱셈 (n = 2), 거듭제곱 (n = 3)으로 시작하는, $H_{n}$ $\mathbb {N}$ 으로 첨수( thiêm sổ )된이항연산 수열이다. 하이퍼 연산 수열의매개변수는 거듭제곱과 유사한 용어를 쓴다; 따라서a는밑,b는지수 (또는하이퍼 지수),n은계수(또는등급)이다..

커누스 윗화살표 표기법을 이용하면, 우리는 하이퍼 연산을 다음과 같이 정의할 수 있다.

H_{n}(a,b)=a\uparrow ^{n-2}b={\begin{cases}b+1&{\text{if }}n=0\\a&{\text{if }}n=1,b=0\\0&{\text{if }}n=2,b=0\\1&{\text{if }}n\geq 3,b=0\\H_{n-1}(a,H_{n}(a,b-1))&{\text{otherwise}}\end{cases}}

(otherwise는 위에 주어진 조건들이 성립하지 않을 때를 뜻한다.)

이는 덧셈, 곱셈, 거듭제곱 다음에 무엇인지에 대한 답으로 해석할 수 있다. 참고로

$a+b=1+(a+(b-1))$
$a\times b=a+(a\times (b-1))$
$a^{b}=a\times (a^{(b-1)})$

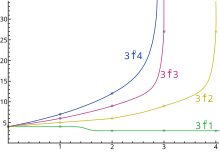
는 하이퍼 연산자들의 관계를 나타내며, 더 높은 연산자들을 정의할 수 있다. 높은 연산자에는 작은 수를 대입해도 매우 큰 숫자가 나온다. 더 자세한 내용을 보려면테트레이션문서를 보라.

일반적으로, 하이퍼 연산자들은 이전 하이퍼 연산자의 반복을 거듭하는 것을 뜻한다. 덧셈, 곱셈, 거듭제곱의 개념은 모두 하이퍼 연산이다; 덧셈 연산은 1을 거듭 더하는 것이고, 곱셈은 한 숫자를 거듭 더하는 것이며, 거듭제곱은 한 숫자를 거듭 곱하는 것이다.

예시

다음은 처음 여섯 개의 하이퍼 연산자이다.

n	연산	정의	이름	영역
0	$b+1$	${1+{\underbrace {1+1+1+\cdots +1} _{b}}}$	hyper0, 증분( tăng phân ),다음수	임의의 b
1	$a+b$	${a+{\underbrace {1+1+1+\cdots +1} _{b}}}$	hyper1,덧셈	임의의 a,b
2	$ab$	${{\underbrace {a+a+a+\cdots +a} } \atop {b}}$	hyper2,곱셈	임의의 a,b
3	$a\uparrow b=a^{b}$	${{\underbrace {a\cdot a\cdot a\cdot a\cdot \ldots \cdot a} } \atop {b}}$	hyper3,거듭제곱	a> 0,b실수, 또는a가 0이 아닌 실수,b가 정수
4	$a\uparrow \uparrow b={}^{b}a$	${{\underbrace {a\uparrow a\uparrow a\uparrow \cdots \uparrow a} } \atop {b}}$	hyper4,테트레이션	a> 0, 정수b≥ −1
5	$a\uparrow \uparrow \uparrow b=a\uparrow ^{3}b$	${{\underbrace {a\uparrow \uparrow a\uparrow \uparrow \cdots \uparrow \uparrow a} } \atop {b}}$	hyper5,펜테이션	a와b는 정수,a> 0,b≥ 0
6	$a\uparrow \uparrow \uparrow \uparrow b=a\uparrow ^{4}b$	${{\underbrace {a\uparrow ^{3}a\uparrow ^{3}\cdots \uparrow ^{3}a} } \atop {b}}$	hyper6, 헥세이션	a와b는 정수,a> 0,b≥ 0

하이퍼 연산의 역사

하이퍼 연산이 맨 처음으로 토론된 경우는 1914년알베르트 베네트가 "가환 하이퍼 연산" 에 대한 이론을 개발했을 때이다. 약 12년 후,빌헬름 아커만이 하이퍼 연산 수열과 어느 정도 연관성이 있는 함수 $\phi (a,b,n)$ ^[1] 를 정의했다. 원래아커만 함수는 같은 반복 규칙을 사용했지만, 현대 하이퍼 연산과 최소 2가지의 다른 점이 있다. 그리고 1947년,Reuben Goodstein^[2]은 하이퍼 연산을 현재 쓰이는 방법으로 정의하였다. 그는 $G(n,a,b)$ 와 같은 기호를 사용했는데, 이는커누스 윗화살표 표기법에서는 $a\uparrow ^{n-2}b$ 와 같다. 또한, Goodstein은 "테트레이션", "펜테이션", "헥세이션" 등 거듭제곱 이상의 연산에 명칭을 부여했다.

표기법

다음 목록은 하이퍼 연산을 표기하는 여러 가지 방법이다.

이름	표기법	비고
기본화살표 표기법	$a\uparrow ^{n-2}b=H_{n}(a,b)$	커누스가 최초로 사용^[3]
굿스틴의 표기법	$G(n,a,b)$	굿스틴(Goodstein)이 최초로 사용^[2]
초기아커만 함수	$A(a,b,n-1)=H_{n}(a,b)$	하이퍼 연산과는 약간 다르다.
현대아커만 함수	$A(n,b-3)+3=H_{n}(2,b)$	밑이 2일 때의 하이퍼 연산과 동일하다.
냄비어의 표기법	$a\otimes ^{n}b$	냄비어(Nambiar)가 최초로 사용^[4]
상자 표기법	$a{\,{\begin{array}{\|c\|}\hline {\!n\!}\\\hline \end{array}}\,}b$	Rubtsov과 Romerio가 최초로 사용^[5]
어깨글자 표기법	$a{}^{(n)}b$	로버트 무나포(Robert Munafo)가 최초로 사용^[6]
아래글자 표기법	$a{}_{(n)}b$	작은 하이퍼 연산을 위해 무나포가 최초로 사용^[6]
ASCII 표기법	`a [n] b`	많은 온라인 포럼에서 사용; 상자 표기법을 기본으로 함.