Realusis skaičius

Geometrinė realiųjų skaičių interpretacijaskaičių tiesėje.

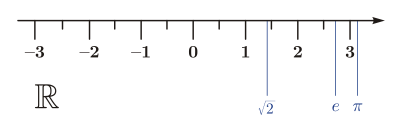
Realieji skaičiai– visiracionaliejiiriracionalieji skaičiai.Begalinėje skaičiųtiesėjekiekvienastaškasatitinka realųjį skaičių. Realiųjų skaičių pavyzdžiai: 0, 2, −1/3, √2,ln 2,πirskaičius e.

Realiųjų skaičiųaibėžymima$\mathbb {R}$.$\mathbb {R} ^{n}$žymin-matę realiųjų skaičių erdvę.

Realusis skaičius vadinamas suskaičiuojamu, jei yraalgoritmas,pagal kurį galima suskaičiuoti po kablelio esančiusskaitmenis.Kadangi algoritmų aibė yraskaiti,o realiųjų skaičių aibė – neskaiti, dauguma realiųjų skaičių nėra suskaičiuojami.

Istorija

Apie 500 m. pr. m. e.pitagorininkaipastebėjo, kadkvadratokraštinė irįstrižainėyra nesuderinami, t. y., nėra tokios atkarpos, kuriai kraštinės ir įstrižainės ilgiai būtų natūralieji kartotiniai. Šiandieniniais terminais tai reiškia, kad nėra tokio racionalaus skaičiaus, kuris būtų kvadrato įstrižainės ir jo kraštinės ilgio santykis. Taip buvo parodytas skaičiaus iracionalumas.

Nuo seniausių laikų žinomasskaičius pi,kuris apibrėžiamas kaipapskritimo ilgioir joskersmenssantykis taip pat pasirodė esąs iracionalusis skaičius, tai 1767 m. įrodė Johanas Lambertas. Kiekvienas atrastas iracionalumas kūrė spragą arba tarpą racionaliųjų skaičių aibėje. Realiųjų skaičių aibės įvedimas šiuos tarpus užpildo. Pirmoji sėkminga realiųjų skaičių konstrukcija laikomaEudoksoproporcijų teorija, aprašytaEuklidoPradmenyse.Nors pati pirmoji formalų realiųjų skaičių formuluotė buvo pasiūlyta vokiečių matematiko Ričardo Dedekindo, naudojant racionaliuosius skaičius ir Dedekindo pjūvį, aksiominį iracionaliųjų skaičių apibrėžimo metodą.

Savybės

Realiųjų skaičių savybės:

• $a+b=b+a$(sumos perstatymo dėsnis)
• $a+(b+c)=(a+b)+c$(sumos jungimo dėsnis)
• $a\cdot b=b\cdot a$(daugybos perstatymo dėsnis)
• $a\cdot (b\cdot c)=(a\cdot b)\cdot c$(daugybos jungimo dėsnis)
• $a\cdot (b+c)=a\cdot b+a\cdot c$(daugybos skirstymo dėsnis)
• su bet kokiu skaičiumi$a$teisingos lygybės$a+0=a,a\cdot 0=0,a\cdot 1=1=a$

Šaltiniai

Vikižodynas