Инјективна функција

Инјекција.Максимум една стрелка до секој елемент во кодоменот B (од елемент од доменот А).

Воматематиката,инјективна функцијаефункцијаf:A→Bако различни елементи одAсе пресликуваат во различни елементи одB,односно за секој елементbодкодоменотBпостоинајмногу еденелементaоддоменотАтаков штоf(a)=b.

Терминотинјективности сродните терминисирјективностибијективностбеа воведени од страна на Никола Бурбаки (Nicholas Bourbaki)(и група други, главно француски математичари од 20 век) кој почнувајќи од 1935 година напиша серија книги за презентирање на модерната напредна математика.

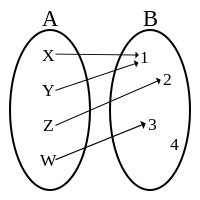
Не е инјекција.Постои елемент во кодоменот В со две стрелки од (различни) елементи од доменот А.

Основни својства

Формално имаме:

$f:A\rightarrow B$е инјективна функција ако$\forall a_{1},\,a_{2},\in A,\,\,\,\,a_{1}\neq a_{2}\,\,\Rightarrow \,\,f(a_{1})\neq f(a_{2})$или еквивалентно

$f:A\rightarrow B$е инјективна функција ако$\forall a_{1},\,a_{2},\in A,\,\,\,\,f(a_{1})=f(a_{2})\,\,\Rightarrow \,\,a_{1}=a_{2}$

Елементот$a$се викапретсликана елементот$b$.Претслика на секој елемент во кодоменот на една инјекцијанемора да постои. Во првата слика, елементот {4} нема претслика. Baжно е да има максимум една претслика. (Види и:Сурјективна функција,Бијективна функција)

• Една од најважните особини на инјективните функции е тоа декаинверзнарелација на инјективна функција е функција, т.н.инверзна функција.Инверзни функции како што еквадратен корен,логаритамска функција,... имаат многу голема улога во математиката.

Кардиналност

Кардиналноста на едно множество е мерка набројот на елементитево множеството. На пример, акоA={X,Y,Z,W}, тогаш кардиналноста наАе 4 и пишуваме #A=4.

• Ако кардиналноста на кодоменот е помала од кардиналноста на доменот, функцијатанее инјекција. (Едноставно кажано, нема начин да се пресликаат 6 елементи во 5 елементи без дупликат.)

Примери

Елементарни функции

Некаf(x):ℝ→ℝ е реална функцијаyод реален аргументx.(Значи влез и излез се броеви.)

• Графичко толкување:функцијатаfе инјективна ако секоја хоризонтала права го пресекува графиконот наfвонајмногу еднаточка (една или ниедна).
• Алгебарско толкување:функцијатаfе инјективна акоf(x_o)=f(x₁) значиx_o=x₁.

Пример:Линеарната функција на која било коса права е инјективна, односноy=ax+bкаде штоa≠0 е инјекција (и сурјекција, така што е бијекција). (Видилинеарна функција.)

Доказ: Некаx_oиx₁се реални броеви. Претпоставиме дека се пресликуваат во истиот број, т.е.a·x_o+b=a·x₁+b.Следуваa·x_o=a·x₁.Бидејќиa≠0, следуваx_o=x₁.Значи кои било два броеви кои се пресликуваат во истиот број се исти. Докажано е дека функцијатаy=ax+bкаде штоa≠0 е инјективна.

Пример:Кубната полиномна функција f(x)=x³е инјективна. Меѓутоа, кубната полиномна функција f(x)=x³–3xне е инјективна.

Дискусија 1: Која било хоризонтална права го пресекува графиконот на

f(x)=x³точно еднаш. (Оваа функција е и сурјективна.)

Дискусија 2: На пример,y_o=2 има две предслики:x=–1 иx=2, а всушност за секојy,–2≤y≤2 функцијата

f(x)=x³–3xима повеќе од една претслика, т.е. повеќе од еденxтаков штоf(x)=y.)

Пример:Квадратната функција f(x) =x²не е инјективна. Двата броевиx=2 иx=-2 се пресликуваат во {4} со што е докажано дека оваа функција не е инјективна. (Оваа функција не е ниту сурјективна.)

Забелешка: Со ограничување на доменот, честопати можеме да дефинираме нова функција која е инјективна. На пример, со ограничување на доменот на квадратната функција имаме „нова “функција, f_/[0,+∞)(x):[0,+∞) → ℝкаде што f_/[0,+∞)(x) =x²која сега е инјективна функција. Оваа функција се викарестрикцијатанаfдо [0,+∞).

Пример:Експоненцијалната функција f(x) = 10^xе инјективна. (Оваа функција не е сурјективна.) Дискусија: Која било хоризонтална права над х-оската го пресекува графиконот на 10^xточно еднаш, а останатите хоризонтални прави не го сечат графиконот ниту еднаш.

Забелешка: Инјективноста на експоненцијална функција може да се користи на следниот начин:

$a^{x_{0}}=a^{x_{1}}\,\,\Rightarrow \,\,x_{0}=x_{1},\,a>0$односно

Пример:$100=10^{x-3}\,\,\Rightarrow \,\,2=x-3\,\,\Rightarrow \,\,x=5$

Инјекција.f(x):ℝ→ℝ (и сурјекција)	Инјекција.f(x):ℝ→ℝ (и сурјекција)	Не е инјекција.f(x):ℝ→ℝ (е сурјекција)
Не е инјекција.f(x):ℝ→ℝ (не е сурјекција)	Инјекција.f(x):ℝ→ℝ (не е сурјекција)	Инјекција.f(x):(0,+∞)→ℝ (и сурјекција)

Други примери со реални функции

Пример:Инверзната функција на 10^x,односнологаритамската функција со основа 10,f(x):(0,+∞)→ℝ дефиниранa соf(x)=log(x) односноy=log(x) е инјективна (и сурјективна).

• Доколку двете множестваAиBимаат повеќе од еден елемент, проекцијата наДекартов производA×Bна еден од неговите фактори никогашнее инјективна функција.

Дискусија: Кардиналноста наA×Bе поголема од кардиналноста наAилиB.

Поврзано

• Функција
• Сурјективна функција
• Бијективна функција

Надворешни врски

• „Injective, Surjective, Bijective “(англиски). 2013.Посетено на 1 декември 2013.интерактивен квиз
• „Injectivity, Surjectivity “(англиски). Wolfram Alpha. Архивирано одизворникотна 2013-11-25.Посетено на 1 декември 2013.интерактивно