Asimant

Unaimant(var.asimant[1]) es un objècte capable de produrre uncamp magneticexterior. Aqueu fenomène, consequéncia de proprietats particulari au sen de lamatèriamagnetica, s'ob sắc rva mai que mai per l'aparicion d'unafòrçad'atraccion sobre luobjectès ferromagnetics.A un ròtle crucial dins mai d'unatecnologiamodèrna.
Dos tipes d'aimant son conoissuts despí l'Antiquitat.Lo premier es l'aimant permanent que non necessita una activacion exteriora per generar lo sieu camp magnetic. Quaucuminerausferróspresentan aquela proprietat coma lamagnetita,mas es finda possible de fabricar d'aimants permanents a partir de materiaus causits. La segonda categoria d'aimants es l'aimant temporari qu'a besonh d'una activacion exteriora per produrre un camp magnetic. Luelectroaimants,fòrça utilizats dins l'industria,fan partida d'aquela familha.
L'estudi dei aimants es un domeni important de lafisica.Donèt naissença aumagnetismee a l'electromagnetismeque son doi brancas centrali deisciénciasmodèrni. De mai, encuèi, son encara l'objècte de recèrcas importanti a causa dei aplicacions nombroï dei aimants tant dins li tecnologias actuali que dins lu projèctes en cors de desvolopament. Ensinda, divèrsi familhas d'aimants son estadi desvolopadi.
Istòria
[modificar|Modificar lo còdi]D'observacions dei proprietats magnetiqui de lamagnetitason atestadi pendent l'Antiquitatdins mai d'una region. En particular, de documents escrichs mòstran una conoissença generala de sieui proprietats, comprés aquela de transmetre la possibilitat de crear uncamp magnetica un tròç defèrre,enChina,enGrècia,enAnatoliae, pus tard, dins l'Empèri Roman[2][3].Li proprietats magnetiqui de l'ambrefretat èran finda conoissudi per lu Grècs[4].Totun, durant de sắc gles, lomagnetismenon aguèt d'aplicacions vertadieri, mas coma totplen demineraus,foguèt associada a lamagia[5].
La promiera aplicacion dei aimants foguèt labóssola,inventada per lu Chinés dins lo corrent dau sắc gle XI[6][7].Lo dispositiu si difondèt lòng dei rotas marchandi e foguèt pauc a pauc adoptat per luArabse per luEuropeus[8][9].Aguèt un ròtle central dins li expedicions maritimi menadi per lu explorators europeus a partir de la segonda mitat dau sắc gle XV. Per exemple, la bóssola es sovent considerada coma un dei factors aguent permés lo succès dei expedicions deCristòl ColombenAmèrica[10].Totun, lu aimants naturals utilizats avian lo defaut de perdre pauc a pauc la sieua aimantacion. Aqueu problema foguèt reglat en lo 1743 perDaniel Bernoulli(1700-1782) emb l'invencion dau promier aimant en forma de fèrre de cavau. Format de doi pòles plaçats a proximitat, garda li sieui proprietats car lu doi camps magnetics mantènon l'aimantacion[11].
En lo 1600, lo fisician anglésWilliam Gilbert(1544-1603) destrièt còrs electric e magnetic. Notèt li lèis d'atraccion e de repulsion dei aimants, l'influéncia de lacalorsus lo magnetisme dau fèrre e assimilèt laTèrraa un aimant.Charles-Augustin Coulomb(1736-1806) posquèt explicar lo foncionament de lafòrçad'atraccion e de repulsion en lo 1785 eHans Christian Orsted(1777-1851) l'associèt a l'electricitat en lo 1805. Pi, 15 ans pus tard, observèt la deviacion d'una agulha magnetizada per uncorrent electric.La mema annada,André-Marie Ampère(1775-1836) magnetizèt un tròç de fèrre plaçat dins un solenoïde somés a un corrent[12].Aquelu trabalhs permetèron pauc a pauc de definir una teoria de l'aimantacion e de produrre d'aimants artificiaus avent d'aplicacions comerciali.
La descripcion fisica dei aimants
[modificar|Modificar lo còdi]Lo camp magnetic
[modificar|Modificar lo còdi]
Lo camp magnetic congreat per un aimant, generalament notat B, es un camp vectorial. Per un ponch donat dins l'espaci, aqueu camp a doi proprietats:
- la sieua direccion es aquela de l'agulha d'una bóssola a l'equilibri.
- lo sieu sens que va dau pòle sud vèrs lo pòle nòrd.
La sieua intensitat es exprimida en A.m-1[13].Totun, per exprimir aquela intensitat, s'utiliza generalament loteslas(T) qu'es en realitat l'unitat dins loSistèma Internacionalde l'induccion magnetica,una grandor permetent de caracterizar l'intensitat e la reparticion espaciala daucamp magnetic.Logauss(G) pòu finda èstre utilizat car la sieua valor, 1 T = 10 000 G, es pus adaptada ai valors observadi dins l'environament terrèstre[14].Per exemple, lo camp magnetic terrèstre vau 58 µT ò 0,58 G a 50° de latituda. Un aimant pichin a un camp magnetic de l'òrdre de 2 000 a 4 000 G, un aimant d'IRMde 15 000 a 30 000 G e lu aimants umans pu poderós de 600 000 G. Lo tesla es mièlhs adaptat per lu fenomènesastronomics.Per exemple, unaestela de neutronspòu facilament aver un camp magnetic de 10 MT.
Lo moment magnetic
[modificar|Modificar lo còdi]Lomoment magnetices una grandor vectoriala, generalament notadaµòM,que s'exprimisse en A.m²[15].Permet de caracterizar l'intensitat d'una fònt magnetica (corrent electric,objecte aimantat...). L'aimantacion es la distribucion espaciala dau moment magnetic. Per un còrs plaçat dins la sieua zòna d'influéncia, aqueu moment si manifèsta per la tendéncia que subisse lo còrs a s'alinhar dins lo sens daucamp magnetic.Per exemple, es lo cas de l'agulha d'unabóssolaque s'alinha dins lo sens daucamp magnetic terrèstre.Cau notar que tot objecte aguent un moment magnetic engendra un camp magnetic a l'entorn d'eu.
L'aimantacion
[modificar|Modificar lo còdi]L'aimantaciond'un objècte aimantat es la valor locala dau sieu moment magnetic per unitat de volume[16].Generalament notadaM,s'exprimisse en A.m-1[17].Es un camp vectorial car li sieui intensitat e orientacion pòdon variar en foncion dau ponch causit per li mesurar. Lu aimants de la vida vidanta an generalament una aimantacion de 100 000 A.m-1,cen que correspònde a un moment magnetic de 0,1 A.m² concentrat dins un volume de 1 cm3.Lofèrrepòu facilament aver una aimantacion d'environ 106A.m-1.Aquò explica perqué s'aimanta sensa dificultat.
La modelizacion dei aimants
[modificar|Modificar lo còdi]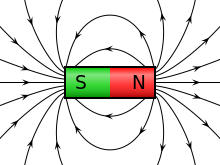
Li a doi biais principals de modelizar lu aimants dins lafisicamodèrna. Lo primier es la representacion basada sus l'existéncia de pòles nòrd e sud. Totun, cau ben nòtar que lu doi pòles dau modèle non correspòndon a de pòles vertadiers. Aquò es unicament un mejan simple per representar lu fenomènes observats ai extremitas d'un aimant. S'un aimant es romput, lo resultat serà la formacion d'aimants pus pichins aguent egalament de pòles nòrd e sud. Dins aqueu modèle, cau utilizar ladivergénciad'un camp de vectors. En simplificant, la divergéncia es un operatormatematicque mesura s'uncamp vectoriauintra ò sòrte d'una zòne de l'espaci. Dins lo nòstre cas, la divergéncia de l'aimantacion ∇Ma l'interior de l'aimant es considerada coma una distribucion de monopòles magnetics. Se la distribucion dei pòles es conoissuda, aquò permet d'obtenir lo camp magneticH.A l'exterior de l'aimant, lo camp magneticBes alora proporcional aH,mentre qu'a l'interior, l'aimantacion deu èstre ajustada aH.
Lo segond metòde de representacion d'un aimant es lo modele d'Ampère.Dins aqueu cas, la magnetizacion es lo resultat de la formacion de corrents microscopics dichs corrents d'Ampère. A l'interior dau materiau, aquelu corrents si compensan e la sieua soma es donc considerada coma nulla. Lu corrents susfacics son ensinda lu contributors unics de l'aimantacion[18].Larègla de la man drechapermet alora de determinar la direccion e lo sens dei particulas portairitz d'una carga positiva.
Li familhas d'aimants
[modificar|Modificar lo còdi]Annèxas
[modificar|Modificar lo còdi]Ligams intèrnes
[modificar|Modificar lo còdi]Bibliografia
[modificar|Modificar lo còdi]Nòtas e referéncias
[modificar|Modificar lo còdi]- ↑Lo Congrès Permanent de la Lenga Occitana, recèrca « aimant », consultat lo 14 de setembre dau 2024,[1].
- ↑Li Shu-hua, « Origine de la Boussole II. Aimant et Boussole »,Isis,vol. 45, n° 2, 1954, pp. 175-196.
- ↑Hugh P. Vowles, « Early Evolution of Power Engineering »,Isis,vol. 17, n° 2, 1932, pp. 412-420.
- ↑David C. Cassidy, Gerald Holton e Floyd James Rutherford,Comprendre la physique,Presses polytechniques et universitaires romandes, 2014, pp. 447-448.
- ↑D. Boorstin,Les découvreurs,París, Seghers, 1986.
- ↑Pierre Juhel,Histoire de la boussole. L'aventure de l'aiguille aimantée,Quae, 2013, pp. 14-15.
- ↑J. M. D. Coey,Magnetism and magnetic materials,Cambridge, Cambridge University Press, 2009, pp. 1–3.
- ↑Petra G. Schmidl, « Two Early Arabic Sources On The Magnetic Compass »,Journal of Arabic and Islamic Studies,vol. 1, 1996-1997, pp. 81-132.
- ↑Pierre Juhel,Histoire de la boussole. L'aventure de l'aiguille aimantée,Quae, 2013, pp. 16.
- ↑Jacques Heers,Christophe Colomb,París, Hachette, 1991, p. 293.
- ↑Karl-Hartmut Müller, Simon Sawatzki, Roland Gauß e Oliver Gutfleisch, J. M. D. Coey e Stuart S. P. Parkin, « Permanent Magnet Materials and Applications »,Handbook of Magnetism and Magnetic Materials,Springer International Publishing, 2021, p. 1391.
- ↑Jean Delaunay,Ampère, André-Marie,vol. 1. Charles Scribner's Sons, 2008, pp. 142–149.
- ↑Michel Dubesset,Le manuel du système international d'unités. Lexique et conversions,Technip, 2000, p. 45.
- ↑Logaussfa partida dausistèma CGS.A un sotamultiple, lo gamma (γ), que vau 1 G = 100 000 γ e que pòu si rescontrar dins de tèxtes ancians. Totun, a la nòstra epòca, lo gamma es estada remplaçada per lo nanotesla (nT).
- ↑Michel Dubesset,Le manuel du système international d'unités. Lexique et conversions,Technip, 2000, p. 92.
- ↑Michel Dubesset,Le manuel du système international d'unités. Lexique et conversions,Technip, 2000, p. 34.
- ↑Michel Dubesset,Le manuel du système international d'unités. Lexique et conversions,Technip, 2000, p. 35.
- ↑Wayne M. Saslow,Electricity, Magnetism, and Light,Academic Press, 2002, p. 426.
