Spațiu tridimensional

Unspațiu tridimensional,spațiu cu trei dimensiunisau3-spațiueste unspațiugeometric în care sunt necesare trei valori (numitecoordonate) pentru a determina poziția unuipunct). Acesta este sensul informal al termenuluidimensiune.

Înfizicășimatematică,osecvențădennumere realepoate fi considerată o locație într-un spațiun-dimensional. Cândn= 3, mulțimea tuturor acestor locații se numeștespațiu euclidiantridimensional(sau pur și simpluspațiu euclidiancând contextul este clar). Este reprezentat în mod obișnuit de simbolul ℝ³.^[1]^[2]Acesta servește ca model cu trei coordonate aluniversuluifizic (adică, partea spațială, fără a lua în considerare timpul), în care există toatămateriacunoscută. Deși acest spațiu rămâne cel mai convingător și util mod de a modela lumea așa cum este percepută experimental,^[3]este doar un exemplu din marea varietate de spații cu trei dimensiuni numite3-varietăți.În acest exemplu clasic, atunci când cele trei valori se referă la măsurători în direcții diferite (coordonate), pot fi alese oricare trei direcții, cu condiția cavectoriicu aceste direcții să nu fie toți în același2-spațiu(plan). De obicei aceste trei valori sunt denumitelungime,lățimeșiînălțime,dar există și alte variante.

În geometria euclidiană

Sisteme de coordonate

Articol principal:Sistem de coordonate.

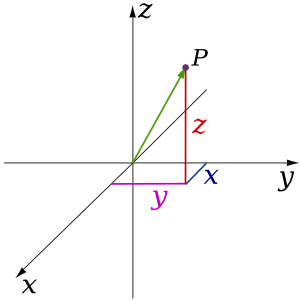
În matematică,geometria analitică(numită și „geometrie carteziană” ) descrie fiecare punct din spațiul tridimensional prin intermediul a trei coordonate. Se dau treiaxe de coordonate,fiecare perpendiculară pe celelalte două în origine, punctul în care se intersectează. De obicei sunt etichetatex,yșiz.În raport cu aceste axe, poziția oricărui punct din spațiul tridimensional este dată de un triplet ordonat de numere reale, fiecare număr oferind distanța acelui punct de la origine, măsurată de-a lungul axei date, care este egală cu distanța acelui punct de planul determinat de celelalte două axe.^[4]

Alte metode de descriere a localizării unui punct în spațiul tridimensional sunt sistemele decoordonate cilindriceșicoordonate sferice,dar există un număr infinit de metode posibile. Mai jos sunt imagini cu sistemele menționate mai sus.

Drepte și planuri

Două puncte diferite determină întotdeauna odreaptă.Trei puncte diferite suntcoliniaresau determină un plan unic. Pe de altă parte, patru puncte diferite pot fi fiecoliniare,fiecoplanare,fie pot determina întregul spațiu.

Două drepte diferite pot fi fieconcurente,fieparalele,fienecoplanare.Două drepte paralele sau două drepte concurente se află într-un plan unic, deci dreptele necoplanare sunt drepte care nu se întâlnesc și nu se află într-un plan comun.

Două plane diferite se pot intersecta într-o dreaptă comună sau sunt paralele (adică nu se întâlnesc). Trei plane diferite, dintre care nici o pereche nu sunt paralele, se pot întâlni fie într-o dreaptă comună, fie într-un punct comun unic, fie nu au niciun punct comun toate trei. În ultimul caz, cele trei drepte de intersecție ale fiecărei perechi de plane sunt reciproc paralele.

O dreaptă poate fi situată într-un plan dat, poate intersecta acel plan într-un punct unic sau poate fi paralelă cu planul. În ultimul caz, vor exista drepte în plan care sunt paralele cu dreapta dată.

Unhiperplaneste un subspațiu cu o dimensiune mai mică decât dimensiunea spațiului complet. Hiperplanele unui spațiu tridimensional sunt subspații bidimensionale, adică plane. În ceea ce privește coordonatele carteziene, punctele unui hiperplan satisfac o singurăecuație liniară,deci planele din acest 3-spațiu sunt descrise prin ecuații liniare. O dreaptă poate fi descrisă de o pereche de ecuații liniare independente — fiecare reprezentând un plan având această dreaptă drept intersecția lor.

Teorema Varignonafirmă că punctele din mijlocul laturilor oricărui patrulater din ℝ³formează unparalelogramși, prin urmare, sunt coplanare.

Sfere și bile

Articol principal:Sferă.

Osferăîn 3-spațiu (numită și2-sferădeoarece este un obiect bidimensional) constă din mulțimea tuturor punctelor din 3-spațiu la o distanță fixă,r,de un punct central $P$ .Interiorulsferei se numeștebilă(sau, aici mai exact, o3-bilă). Volumul bilei este dat de:

V={\frac {4}{3}}\pi r^{3}

.

Un alt tip de sferă apare dintr-o 4-bilă, a cărei suprafață tridimensională este o3-sferă:puncteechidistantede originea spațiului euclidian ℝ⁴.Dacă un punct are coordonatele $P$ (x,y,z,w), atunci $x^{2}+y^{2}+z^{2}+w^{2}=1\,$ caracterizează punctele de pe 3-sfera unitate(centrată în origine).

Politopuri

Articol principal:Poliedru.

În trei dimensiuni există nouă politopuri regulate: cele cincipoliedre platoniceși cele patru stelate,poliedrele Kepler–Poinsot.

Politopuri regulate tridimensionale
Clasa	Poliedre platonice					Poliedre Kepler–Poinsot
Simetrie	T_d	O_h		I_h
Grup Coxeter	A₃,[3,3]	B₃,[4,3]		H₃,[5,3]
Ordin	24	48		120
Poliedru regulat	{3,3}	{4,3}	{3,4}	{5,3}	{3,5}	{5/2,5}	{5,5/2}	{5/2,3}	{3,5/2}

Suprafețe de revoluție

Articol principal:Suprafață de revoluție.

Osuprafațăgenerată prin rotirea uneicurbeplane în jurul unei drepte fixe în planul său ca axă se numeștesuprafața de revoluție.Curba plană se numeștegeneratoareasuprafeței. Osecțiune a suprafeței,realizată prin intersecția suprafeței cu un plan perpendicular (ortogonal) pe axă, este un cerc.

Exemple simple se obțin atunci când generatoarea este o dreaptă. Dacă dreapta generatoare intersectează axa, suprafața de revoluție este unconcu vârful (apexul) în punctul de intersecție. Dacă generatoarea și axa sunt paralele, atunci suprafața de revoluție este uncilindru.

Cuadrice

Articol principal:Cuadrică.

Analog cuconicele,ansamblul de puncte ale căror coordonate carteziene satisfac ecuația generală de gradul al doilea, și anume,

Ax^{2}+By^{2}+Cz^{2}+Fxy+Gyz+Hxz+Jx+Ky+Lz+M=0,

unde $A, B, C, F, G, H, J, K, L$ și $M$ sunt numere reale și nu toate dintre $A, B, C, F, G$ și $H$ sunt zero, se numesștecuadrică.^[5]

Există șase tipuri de cuaricenedegenerate:

Cuadricele degenerate pot fi mulțimea vidă, un singur punct, o singură dreaptă, un singur plan, o pereche de plane sau un cilindru pătratic (o suprafață constând dintr-o secțiune conică nedegenerată într-un plan $\pi \,$ și toate dreptele din ℝ³prin acea conică care suntnormalepe $\pi.$ ^[5]Conurile eliptice sunt uneori considerate și ele a fi cuadrice degenerate.

Hiperboloidul cu o pânză este osuprafață riglată,ceea ce înseamnă că poate fi generat de o familie de drepte. De fapt, are două familii de drepte generatoare, membrii fiecărei familii sunt disjuncti și fiecare membru intersectează, cu o singură excepție, fiecare membru al celeilalte familii.^[6]

În algebra liniară

Un alt punct de vedere cu privire la spațiul tridimensional se găsește înalgebra liniară,unde ideea de independență este esențială. Spațiul are trei dimensiuni deoarece lungimea unuiparalelipiped dreptunghiceste independentă de lățimea sau înălțimea sa. În limbajul algebrei liniare spațiul este tridimensional deoarece fiecare punct din spațiu poate fi descris printr-o combinație liniară de trei valori (vectorcu trei componente).

Produs scalar, unghi și lungime

Articol principal:Produs scalar.

Un vector poate fi reprezentat ca o săgeată. Modulul vectorului este lungimea sa, iar direcția sa este direcția indicată de săgeată. Un vector din ℝ³poate fi reprezentat printr-un triplet ordonat de numere reale. Aceste numere sunt denumite „componentele” vectorului.

Produsul scalaral doi vectori $\mathbf {A} =A_{1},A_{2},A_{3}\,$ și $\mathbf {B} =B_{1},B_{2},B_{3}\,$ este definit drept:^[7]

\mathbf {A} \cdot \mathbf {B} =A_{1}B_{1}+A_{2}B_{2}+A_{3}B_{3}.

Modulul vectorului $\mathbf {A}$ este notat cu $\|\mathbf {A} \|$ .Produsul scalar al vectorului $\mathbf {A} =A_{1},A_{2},A_{3}\,$ cu el însuși este:

\mathbf {A} \cdot \mathbf {A} =\|\mathbf {A} \|^{2}=A_{1}^{2}+A_{2}^{2}+A_{3}^{2},

adică

\|\mathbf {A} \|={\sqrt {\mathbf {A} \cdot \mathbf {A} }}={\sqrt {A_{1}^{2}+A_{2}^{2}+A_{3}^{2}}},

care este formulalungimii euclidienea vectorului.

Fără a se referi la componentele vectorilor, produsul scalar al a doi vectori euclidieni diferiți de zero $\mathbf {A}$ și $\mathbf {B}$ este dat de:^[8]

\mathbf {A} \cdot \mathbf {B} =\|\mathbf {A} \|\,\|\mathbf {B} \|\cos \theta,

unde $θ$ esteunghiuldintre $A$ și $B$ .

Produs vectorial

Articol principal:Produs vectorial.

Produsul vectorialal doi vectori $\mathbf {A}$ și $\mathbf {B}$ este un vector în spațiul tridimensional. Operația este notată prin simbolul ×. Produsul $\mathbf {A} \times \mathbf {B}$ esteperpendicularpe ambii $\mathbf {A}$ și $\mathbf {B}$ ,adică este normal pe planul care-i conține pe ambii. Are multe aplicații în matematică,fizicășiinginerie.

Spațiul și produsul formează oalgebră peste un corp,care nu este nicicomutativ,niciasociativ,dar este oalgebră Lie,produsul vectorial fiind oparanteză Lie.

Într-unn-spațiu se poate folosi produsul an– 1 vectori pentru a genera un vector perpendicular pe toți. Dar dacă produsul este limitat la produse binare nebanale cu rezultate vectoriale, acesta există doar în trei și șapte dimensiuni.^[9]

În calcule

Articol principal:Calcul vectorial.

Gradient, divergență și rotor

Într-un sistem de coordonate rectangular,gradientuleste dat de:

\nabla f={\frac {\partial f}{\partial x}}\mathbf {i} +{\frac {\partial f}{\partial y}}\mathbf {j} +{\frac {\partial f}{\partial z}}\mathbf {k}

Divergențaunuicâmp vectorialcontinuu derivabilF=Ui+Vj+Wkeste egală cu funcțiascalară:

\operatorname {div} \,\mathbf {F} =\nabla \cdot \mathbf {F} ={\frac {\partial U}{\partial x}}+{\frac {\partial V}{\partial y}}+{\frac {\partial W}{\partial z}}.

Dezvoltat în coordonate carteziene,rotorul∇ ×Feste, pentruFcompus din [F_x,F_y,F_z]:

{\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\\\{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial y}}&{\frac {\partial }{\partial z}}\\\\F_{x}&F_{y}&F_{z}\end{vmatrix}}

undei,j,andksuntversoriipe axelex,y,respectivz.Dezvoltarea este:^[10]

\left({\frac {\partial F_{z}}{\partial y}}-{\frac {\partial F_{y}}{\partial z}}\right)\mathbf {i} +\left({\frac {\partial F_{x}}{\partial z}}-{\frac {\partial F_{z}}{\partial x}}\right)\mathbf {j} +\left({\frac {\partial F_{y}}{\partial x}}-{\frac {\partial F_{x}}{\partial y}}\right)\mathbf {k}

Integrale, integrale de suprafață și integrale de volum

Pentru uncâmp scalarf:U⊆Rⁿ→R,integrala curbei continueC⊂Ueste definită drept

\int \limits _{C}f\,ds=\int _{a}^{b}f(\mathbf {r} (t))|\mathbf {r} '(t)|\,dt.

under:[a, b] →Ceste o parametrizarebijectivăa curbeiCastfel încâtr(a) șir(b) să fie capetele luiCiar $a<b$ .

Pentru un câmp vectorialF:U⊆Rⁿ→Rⁿ,integrala curbei continueC⊂Uîn direcția luireste definită drept

\int \limits _{C}\mathbf {F} (\mathbf {r} )\cdot \,d\mathbf {r} =\int _{a}^{b}\mathbf {F} (\mathbf {r} (t))\cdot \mathbf {r} '(t)\,dt.

unde · este produsul scalar iarr:[a, b] →Ceste o parametrizare bijectivă a curbeiCastfel încâtr(a) șir(b) să fie capetele luiC.

Ointegrală de suprafațăeste o generalizare aintegralei multiplela integrarea peSuprafață.Se poate considera că este analoagaintegralei duble.Pentru a găsi o formulă explicită pentru integrala de suprafață, trebuie parametrizată suprafațaS,luând în considerare un sistem decoordonate curbiliniipeS,calatitudine și longitudinepe osferă.Fie o astfel de parametrizarex(s,t), unde (s,t) variază în anumite regiuniTdin plan. Apoi, integrala de suprafață este dată de:

\iint _{S}f\,\mathrm {d} S=\iint _{T}f(\mathbf {x} (s,t))\left\|{\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right\|\mathrm {d} s\,\mathrm {d} t

unde expresia dintre bare din partea dreaptă estemagnitudineaprodusului vectorial alderivatelor parțialex(s,t) și este cunoscută sub numele de suprafațaelementului.Fiind dat un câmp vectorialvpeS,aceasta este o funcție care atribuie fiecăruixdinSun vectorv(x), integrala de suprafață poate fi definită în funcție de componente conform definiției integralei de suprafață a unui câmp scalar; rezultatul este un vector.

Ointegrală de volumeste o integrală pe un domeniu tridimensional. Poate însemna și ointegrală triplăîntr-o regiuneDdinR³a funcției $f(x,y,z),$ și este exprimată prin:

\iiint \limits _{D}f(x,y,z)\,dx\,dy\,dz.

Teorema gradientului

Teorema gradientuluiafirmă că integrala unui gradient poate fi calculată din valorile câmpului scalar original la capetele curbei. Fie $\varphi:U\subseteq \mathbb {R} ^{n}\to \mathbb {R}$ .Atunci:

\varphi \left(\mathbf {q} \right)-\varphi \left(\mathbf {p} \right)=\int _{\gamma [\mathbf {p},\,\mathbf {q} ]}\nabla \varphi (\mathbf {r} )\cdot d\mathbf {r}.

Teorema Kelvin–Stokes

Teorema Kelvin–Stokesleagă integrala de suprafață a rotorului unui câmp vectorial F pe suprafața euclidiană tridimensională Σ de integrala câmpului vectorial pefrontierasa, ∂Σ:

\iint _{\Sigma }\nabla \times \mathbf {F} \cdot \mathrm {d} \mathbf {\Sigma } =\oint _{\partial \Sigma }\mathbf {F} \cdot \mathrm {d} \mathbf {r}.

Teorema divergenței

Presupunând că $V$ este o submulțime a $\mathbb {R} ^{n}$ (în cazul $n=3,V\,$ reprezintă un volume în 3-spațiu) care este compactă și are frontiera netedă pe porțiuni $S$ (notată și $\delta V=S)$ .Dacă $F$ este un câmp vectorial continuu derivabil definit în vecinătatea lui $V$ ,atunciteorema divergențeiafirmă că:^[11]

\iiint _{V}\left(\mathbf {\nabla } \cdot \mathbf {F} \right)\,dV=

$\oiint$

\scriptstyle S

(\mathbf {F} \cdot \mathbf {n} )\,dS.

Partea stângă este integrala de volum pe volumul $V$ ,partea dreaptă este integrala de suprafață pe limita volumului $V$ .Varietatea închisă $\partial V$ este, în general, frontiera lui $V$ ca suprafață normalăorientatăspre exterior, iar $n$ este câmpul unitate normal orientat spre exteriorul frontierei $\partial V$ .(notația $d S$ poate fi folosită ca o prescurtare pentru $n dS$ .)

În topologie

Spațiul tridimensional are o serie de proprietăți topologice care îl disting de spațiile cu alte numere de dimensiuni. De exemplu, sunt necesare cel puțin trei dimensiuni pentru a face unnodîntr-o bucată de sfoară.^[12]

Îngeometria diferențialăspațiile tridimensionale generice sunt3-varietăți,care seamănă local cu ${\mathbb {R} }^{3}$ .

În geometria finită

Multe idei cu privire la dimensiuni pot fi testate îngeometria finită.Cea mai simplă formă estePG (3,2),care areplane Fanoca subspații bidimensionale. Este o formă dingeometria Galois,un studiu algeometriei proiectivefolosindcâmpuri finite.Astfel, pentru orice câmp Galois GF(q), există unspațiu proiectivPG(3,q) cu trei dimensiuni. De exemplu, oricare trei drepte neconcurente din PG(3,q) sunt conținute în exact unregulus.^[13]

Note

^en„Compendium of Mathematical Symbols”.Math Vault(în engleză).1 martie 2020.Accesat în12 august 2020.
^en„Euclidean space - Encyclopedia of Mathematics”.encyclopediaofmath.org.Accesat în12 august 2020.
^„Euclidean space | geometry”.Encyclopedia Britannica(în engleză).Accesat în12 august 2020.
^enHughes-Hallett, Deborah; McCallum, William G.; Gleason, Andrew M. (2013).Calculus: Single and Multivariable(ed. 6). John wiley.ISBN 978-0470-88861-2.
^^a ^bBrannan, Esplen & Gray 1999,pp. 34–5.
^Brannan, Esplen & Gray 1999,pp. 41–2.
^Anton 1994,p. 133.
^Anton 1994,p. 131.
^enWS Massey (1983). „Cross products of vectors in higher dimensional Euclidean spaces”.The American Mathematical Monthly.90(10): 697–701.doi:10.2307/2323537.JSTOR 2323537.If one requires only three basic properties of the cross product... it turns out that a cross product of vectors exists only in 3-dimensional and 7-dimensional Euclidean space.
^Arfken, p. 43
^enM. R. Spiegel; S. Lipschutz; D. Spellman (2009).Vector Analysis.Schaum’s Outlines (ed. 2nd). USA: McGraw Hill.ISBN 978-0-07-161545-7.
^enRolfsen, Dale (1976).Knots and Links.Berkeley, California: Publish or Perish.ISBN 0-914098-16-0.
^Albrecht Beutelspacher, Ute Rosenbaum (1998).Projective Geometry,p. 72,Cambridge University Press ISBN: 0-521-48277-1

Bibliografie

enAnton, Howard (1994),Elementary Linear Algebra(ed. 7th), John Wiley & Sons,ISBN 978-0-471-58742-2
enGeorge B. Arfken, Hans J. Weber,Mathematical Methods For Physicists,Academic Press; 6 edition (June 21, 2005).ISBN: 978-0-12-059876-2.
enBrannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1999),Geometry,Cambridge University Press,ISBN 978-0-521-59787-6

Vezi și

Legături externe

Materiale media legate deSpațiu tridimensionallaWikimedia Commons
enEric W. Weisstein,Four-Dimensional GeometrylaMathWorld.
enElementary Linear Algebra - Chapter 8: Three-dimensional GeometryKeith Matthews de la University of Queensland, 1991

Portal Matematică

[1] „Compendium of Mathematical Symbols”.Math Vault(în engleză).1 martie 2020.Accesat în12 august 2020.

[2] „Euclidean space - Encyclopedia of Mathematics”.encyclopediaofmath.org.Accesat în12 august 2020.

[3] „Euclidean space | geometry”.Encyclopedia Britannica(în engleză).Accesat în12 august 2020.

[Hughes-4] Hughes-Hallett, Deborah; McCallum, William G.; Gleason, Andrew M. (2013).Calculus: Single and Multivariable(ed. 6). John wiley.ISBN 978-0470-88861-2.

[Brannan-5] Brannan, Esplen & Gray 1999,pp. 34–5.

[6] Brannan, Esplen & Gray 1999,pp. 41–2.

[7] Anton 1994,p. 133.

[8] Anton 1994,p. 131.

[Massey2-9] WS Massey (1983). „Cross products of vectors in higher dimensional Euclidean spaces”.The American Mathematical Monthly.90(10): 697–701.doi:10.2307/2323537.JSTOR 2323537.If one requires only three basic properties of the cross product... it turns out that a cross product of vectors exists only in 3-dimensional and 7-dimensional Euclidean space.

[10] Arfken, p. 43

[spiegel-11] M. R. Spiegel; S. Lipschutz; D. Spellman (2009).Vector Analysis.Schaum’s Outlines (ed. 2nd). USA: McGraw Hill.ISBN 978-0-07-161545-7.

[12] Rolfsen, Dale (1976).Knots and Links.Berkeley, California: Publish or Perish.ISBN 0-914098-16-0.

[13] Albrecht Beutelspacher, Ute Rosenbaum (1998).Projective Geometry,p. 72,Cambridge University Press ISBN: 0-521-48277-1

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

v d m Dimensiuni
Spații dimensionale	Spațiu vectorial Spațiu euclidian Spațiu afin Spațiu proiectiv Modul liber Varietate geometrică Varietate algebrică Spațiu-timp
Alte dimensiuni	Krull Acoperire Lebesgue Inductivă Hausdorff Minkowski Fractală Grad de libertate
Politopurișiforme	Hiperplan Hipersuprafață Hipercub Hiperdreptunghi Ortoplex Semihipercub Hipersferă Simplex
Dimensiuni după număr	Zero Una Două Trei Patru Cinci Șase Șapte Opt Nouă n-dimensiuni Dimensiuni negative
Vezi și	Hiperspațiu
Categorie