Ортогональный базис

Ортонормированный базис в 3-мерномевклидовом пространстве

Ортогона́льный (ортонорми́рованный) ба́зис—ортогональная(ортонормированная) система элементовлинейного пространствасоскалярным произведением,обладающая свойствомполноты.

Конечномерный случай

Мнемоническое правило для определения ориентации базиса. Слева — левоориентированный базис, справа — правоориентированный.

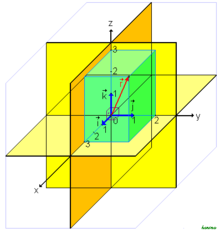
Ортогональный базис—базис,составленный из попарноортогональныхвекторов. Ортонормированный базисудовлетворяет ещё и условию единичностинормывсех его элементов. То есть это ортогональный базис с нормированными элементами.

Последнее удобно записывается при помощисимвола Кронекера:

$(e_{i},e_{j})=\delta _{ij},$

то естьскалярное произведениекаждой пары базисных векторов равно нулю, когда они не совпадают ($i\neq j$), и равно единице при совпадающем индексе, то есть когда берется скалярное произведение любого базисного вектора с самим собой.

Очень многое записывается в ортогональном базисе гораздо проще, чем в произвольном, поэтому очень часто стараются использовать именно такие базисы, если только это возможно или использование какого-то специального неортогонального базиса не дает особых специальных удобств. Или если не отказываются от него в пользу базиса общего вида из соображений общности.

Ортонормированный базис является самодуальным (дуальныйему базис совпадает с ним самим). Поэтому в нём можно не делать различия между верхними и нижними индексами, и пользоваться, скажем, только нижними (как обычно и принято, если конечно при этом используются только ортонормированные базисы).

Линейная независимость следует из ортогональности, то есть достигается для ортогональной системы векторов автоматически.

Коэффициенты в разложении вектора по ортогональному базису:

$\ \mathbf {a} =a_{1}\mathbf {e_{1}} +a_{2}\mathbf {e_{2}} +\ldots +a_{n}\mathbf {e_{n}}$

можно найти так:

$\ a_{i}={\frac {(\mathbf {a},\mathbf {e_{i}} )}{(\mathbf {e_{i}},\mathbf {e_{i}} )}}.$

Полнота ортонормированной системы векторов эквивалентнаравенству Парсеваля:для любого вектора$\mathbf {a}$квадрат нормы вектора равен сумме квадратов коэффициентов его разложения по базису:

$(\mathbf {a},\mathbf {a} )=\sum _{i}(\mathbf {a},\mathbf {e_{i}} )^{2},$

Аналогичные соотношения имеют место и для бесконечномерного случая (см. ниже).

Бесконечномерный случай

Ортогональный базис— система попарно ортогональных элементов$e_{1},e_{2},...,e_{n},...$гильбертова пространства$X$такая, что любой элемент$x\in X$однозначно представим в виде сходящегося по норме ряда

$x=\sum _{n=1}^{\infty }a_{n}e_{n},$

называемогорядом Фурьеэлемента$x$по системе$\{e_{n}\}$.

Часто базис$\{e_{n}\}$выбирается так, что$|e_{n}|=1$,и тогда он называетсяортонормированным базисом.В этом случае числа$a_{n}$,называются коэффициентами Фурье элемента$x$по ортонормированному базису$\{e_{n}\}$,имеют вид

$a_{n}=(x,e_{n})$.

Необходимым и достаточным условием того, чтобы ортонормированная система$\{e_{n}\}$была базисом, являетсяравенство Парсеваля.

Гильбертово пространство, имеющее ортонормированный базис, являетсясепарабельным,и обратно, во всяком сепарабельном гильбертовом пространстве существует ортонормированный базис.

Если задана произвольная система чисел$\{a_{n}\}$такая, что$\sum _{n=1}^{\infty }a_{n}^{2}<\infty$,то в случае гильбертова пространства с ортонормированным базисом$\{e_{n}\}$ряд$\sum _{n=1}^{\infty }a_{n}e_{n}$— сходится по норме к некоторому элементу$x\in X$. Этим устанавливается изоморфизм любого сепарабельного гильбертова пространства пространству$l_{2}$(теорема Рисса— Фишера).

Примеры

• Стандартный базис$e_{1}=(1,0,\ldots,0)^{\mathrm {T} },e_{2}=(0,1,\ldots,0)^{\mathrm {T} },\ldots e_{n}=(0,0,\ldots,1)^{\mathrm {T} }$в n-мерном евклидовом пространствеRⁿявляется ортонормированным.

• Множество$\{f_{n}={\frac {1}{\sqrt {2\pi }}}e^{inx},n\in \mathbb {Z} \}$образует ортонормированный базис в$L^{2}([-\pi,\pi ])$.

Литература

• Гельфанд И. М.Лекции по линейной алгебре М.: Наука, 1971.
• Морен К.Методы гильбертова пространства. М.: Мир, 1965.

См. также

• Ортонормированная система
• Ортогонализация
• Процесс Грама ― Шмидта
• Флаг (математика)