Klatno

Za ostala značenja, vidiKlatno (razvrstavanje).

Prikaz klatna koje se njiše usledgravitacione sile.Prikazano je inaprezanjeu nitiT.

Kad se klatno pusti, ono se kreće pod uticajem silem∙g∙sin θ.

Fukoovo klatno

Sat s klatnom ili časovnik njihalica iz 1904. godine, vrlo je pouzdana vrstamehaničkog sata.

Gravimetrijaje određivanje poljasile težemerenjemnjenogubrzanjau različitim tačkama naZemlji.

RekonstrukcijaDžang Hengovogseizmografa.

Klatnoilinjihalojefizičko telokoje se njiše okoravnotežnogpoložaja. Njihanje mogu izazvatigravitaciona sila,elastičnasila(na primeropruga),električna sila,magnetnasila i drugo.

Matematičko klatnojematerijalna tačkaobešena o nerastegljivu nit bezmase.Za maleamplitude,periodoscilovanja zavisi odubrzanja sile težegi oddužinenitilna koju jemasaobešena:

$T=2\cdot \pi \cdot {\sqrt {\frac {l}{g}}}\qquad \qquad \qquad (\theta \,manje\,od\,\,5^{\circ })\,$

Fizičko klatnoje fizičko telo koje se njiše oko čvrste tačke koja se ne podudara satežištem.Izvedeno iz položaja ravnoteže, fizičko klatno počinje da se njiše pod uticajem vlastitetežine.Period oscilovanja zavisi od težine tela, udaljenosti između težišta i obesišta i odmomenta inercijes obzirom na obesište.

Torzijsko klatnoje telo koje je obešeno o nit koje se periodično uvrće (rotira) u ravni normalnoj na nit zbog elastične sile niti. Za male amplitude kretanje jeharmonijsko.

Kretanjeklatna prvi su proučavaliGalileo GalilejiLeon Fuko(Fukoovo klatno).

Matematičko klatno

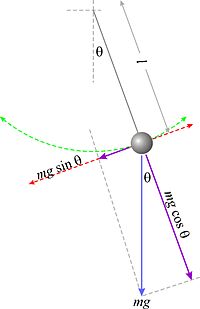
Pričvrsti li se malaolovnakuglica na tanku nit i ako se otkloni za izvestan ugao od njenog ravnotežnog položaja, onda ta kuglica na niti vrlo maletežineprestavlja matematičko klatno. Kuglica se neće zaustaviti u svomravnotežnom položajuveć će oko njegaoscilovati.Put klatna između krajnjih tačaka zove se jednaoscilacija,a vreme koje je potrebno da klatno učini jednu oscilaciju zove seperiodilivreme oscilovanja.Kod oscilovanja klatna vrši se stalno pretvaranjepotencijalne energijeukinetičku energijui obratno. Kad se klatno podigne iz položaja mirovanja na nekuvisinu|h,daje mu se izvesnu potencijalna energija. Kinetička energija je u tom položaju jednaka nuli, jer klatno nemabrzine.Kad se klatno pusti, ono će se pod uticajem komponentem∙g∙sin θkretati, pa će njegova potencijalna energija opadati, a kinetička rasti. U najdonjem položaju (ravnotežnom položaju) biće potencijalna energija jednaka nuli, dok će kinetička energija biti najveća, jer je tu brzina najveća. Zbogtromostiili inercije klatno će produžiti svoje njihanje, te će ponovno kinetička energija opadati, a potencijalna rasti, a u krajnjoj tački ponovno će kinetička energija biti nula, a potencijalna najveća.

Kad ne bi bilo trenja u osloncu i otpora vazduha, klatno bi se stalno njihalo i uvek bi se popelo do iste visine. Međutim, njegova se energija polagano troši naotpor vazduhaitrenje,te titraji postaju sve slabiji, dok se klatno konačno ne umiri u ravnotežnoj tački.Silakoja prouzrokuje njihanje je:

$F=m\cdot g\cdot \sin \theta$

Može se izračunati da je vreme jednog titraja:

$T=2\cdot \pi \cdot {\sqrt {\frac {l}{g}}}$

a vreme jednog njihaja koje je polovina jednog titraja:

$t=\pi \cdot {\sqrt {\frac {l}{g}}}$

Iz ovog izraza proizlazi da trajanje jednog titraja zavisi od dve veličine, od dužine klatnali odubrzanjagsile teže.Prema tome je trajanje jednog titraja:

• srazmerno (proporcionalno) s drugim korenom iz dužine klatnaluz stalnog,to jest što je klatno duže, to je i vreme klatna veće, te se klatno njiše polaganije. Što je klatno kraće, vreme titraja je manje i klatno se njiše brže;
• obrnuto srazmerno s ubrzanjem sile težeguz konstantnu vrednostl,to jest gde je ubrzanje sile teže veće, tamo je vreme oscilovanja kraće. Gde je ubrzanje sile teže manje, tamo je i vreme oscilovanja veće.

Trajanje jednog titraja ne zavisi:

• odtežine,to jest o toga da li je klatno lakše ili teže, da li je građeno od željeza, drva, olova ili bilo kojeg drugog materijala;
• odamplitude.To znači da je vreme jednog titraja isto, bez obzira da li se klatno skrene iz položaja ravnoteže za veći ili manjiugao.Praktičko to vredi samo za male uglove približno doθ= 5°.

Fizičko klatno

Primena klatna utehnicije vrlo velika, samo to nije matematičko nego fizičko klatno. Takvo fizičko klatno je svako telo koje se može njihati pod uticajem vlastitetežineoko jedne čvrste tačke koja se zove obesište. Međutim, kad bi bila slobodna, svaka materijalna tačka tog tela imala bi svoje trajanje jednog njihaja koje bi bilo zavisno od njene udaljenosti od obesišta. Znači da bi materijalne tačke toga tela imale različita vremena jedne oscilacije. Kako se one ne mogu odvojiti jedna od druge, celo telo ima neko srednje trajanje oscilacije.

Vreme jednog fizičkog klatna se dobija tako da nađe dužinu onog matematičkog klatna koje se njiše isto tako kao i fizičko klatno. To je pak ono matematičko klatno koje ima istuugaonu brzinuiugaono ubrzanjekao i fizičko klatno. Dužinaloonog matematičkog klatna čije je vreme jedne oscilacije isto kao i kod fizičkog klatna zove seredukovana dužina fizičkog klatna.Ona se može izraziti kao:

$l_{0}={\frac {I}{m\cdot R}}$

gde je:I-moment tromostiilimoment inercijefizičkog klatna s obzirom na obesište,m-masafizičkog njihala, aR- udaljenost između obesišta icentra masa(težišta). Na osnovu toga se dobijavremejedne oscilacije fizičkog klatnaT:

$T=2\cdot \pi \cdot {\sqrt {\frac {I}{m\cdot g\cdot R}}}$

Fizičko klatno se primenjuje kodčasovnika sa klatnom.Ta se primena zasniva na izohronosti, to jest na nezavisnosti vremena oscilacije od amplitude. Klatno svojim pravilnim hodom prisiljavamehanizamizupčanikeda se u jednakim vremenskim razmacima pomiču. Da se zbog trenja i otpora vazduha klatno ne zaustavi, ono dobija nakon svake oscilacije podsticajpritiskomvisećegutega,koji se kod toga odmotava svretena.Budući da trajanje jedne oscilacije zavisi od ubrzanja sile teže, to znači da časovnik sa klatnom neće na svakom mestu ići tačno. Na primer, časovnik koji ide tačno naBalkanuići će sve brže što se više približavapolovima,a polaganije što se više približavaekvatoru.

Sekundno klatno

Kad se u izraz oscilacije matematičkog klatna stavi da jet= 1 sekunda, dobija pretvaranjem:

$g=\pi ^{2}\cdot l$

Takvo klatno kome jedna oscilacija traje jednu sekundu zove sesekundnim klatnom.Dakle, merenjem dužine sekundnog klatna može se određivatiubrzanje sile teže,što ima veliku važnost urudarstvu.Naime, ubrzanje sile teže ne menja se samo sageografskom širinomveć ono pokazuje znatne promene često i na manjem područjuZemlje.To dolazi zbog toga što se ispodZemljine korenalaze mase različitegustine.Mase veće gustine uzrokuju veće ubrzanje sile teže, što proizlazi izNjutnovog zakona gravitacije.Prema veličini ubrzanja sile teže na različitim mestima mogu se stvarati zaključci o vrsti i količini masa, odnosno naslaga koje se nalaze na tim mestima. Prema tome, određivanje ubrzanja sile teže služi za istraživanjeruda.Specijalna klatna koja služe u tu svrhu zovu segravimetri.

Seizmograf

Seizmograf(grč.σεισμός:potres + graf) jemerni instrumentkojim semerei beleže pomaci tla tokompotresa.Glavni je deo seizmografa klatno, koje služi kaosenzorpomakatlai koje zbogtromosti(inercije) nastoji da održi stanje mirovanja za potresa, dok se kućište slobodnokreće,te se beleži razlika njihovog međusobnog položaja (seizmogram).Uređajemza merenje prigušuju se slobodneoscilacijeklatna.Mehaničkeseizmografe nasledili suelektromagnetski,kod kojih se klatno sazavojnicomkreće u stalnommagnetnom poljukućišta te takoindukujeelektrični napon,aelektrični se signalpohranjuje namemorijsku jedinicu.Kako bi se na temelju seizmograma moglo potpuno rekonstruirati kretanje tla, seizmografi istodobno beležetri međusobno normalne komponentekretanja tla.

Literatura

• Borwein, J.M.;Borwein, P.B.(1987).Pi and the AGM.New York: Wiley. str. 1-15.ISBN978-0-471-83138-9.MR0877728.
• Baker, Gregory L.; Blackburn, James A. (2005).The Pendulum: A Physics Case Study.Oxford University Press.
• M. Gitterman (2010).The Chaotic Pendulum(World Scientific).
• Michael R. Matthews, Arthur Stinner, Colin F. Gauld (2005)The Pendulum: Scientific, Historical, Philosophical and Educational Perspectives,Springer
• Matthews, Michael R.; Gauld, Colin; Stinner, Arthur (2005). „The Pendulum: Its Place in Science, Culture and Pedagogy”.Science & Education13(4/5): 261-277.Bibcode2004Sc&Ed..13..261M.DOI:10.1023/b:sced.0000041867.60452.18.
• Schlomo Silbermann,(2014) "Pendulum Fundamental; The Path Of Nowhere" (Book)
• Matthys, Robert J. (2004).Accurate Pendulum Clocks.UK: Oxford University Press.ISBN978-0-19-852971-2.
• Nelson, M. G.; Olsson (februar 1986). „The pendulum – Rich physics from a simple system”.American Journal of Physics54(2): 112-121.Bibcode1986AmJPh..54..112N.DOI:10.1119/1.14703.
• L. P. Pook (2011).Understanding Pendulums: A Brief Introduction(Springer).
• Ochs, Karlheinz (2011). „A comprehensive analytical solution of the nonlinear pendulum”.European Journal of Physics32(2): 479-490.Bibcode2011EJPh...32..479O.DOI:10.1088/0143-0807/32/2/019.
• Sala, Kenneth L. (1989). „Transformations of the Jacobian Amplitude Function and its Calculation via the Arithmetic-Geometric Mean”.SIAM J. Math. Anal.20(6): 1514-1528.DOI:10.1137/0520100.
• Arnold, V.I. (1989).Mathematical Methods of Classical Mechanics.Springer. str. 123.ISBN978-0-387-96890-2.
• Marion, Jerry B.; Thornton, Stephen T. (1995).Classical dynamics of particles and systems(4th izd.). Brooks Cole. str.398-401.ISBN978-0-03-097302-4.
• Persson, Anders O. (2005).„The Coriolis Effect: Four centuries of conflict between common sense and mathematics, Part I: A history to 1885”.History of Meteorology2.Arhivirano izoriginalana datum 11. 4. 2014.Pristupljeno 16. 2. 2019.
• Daliga, K.; Przyborski, M.; Szulwic, J. (2015).„Foucault's Pendulum. Uncomplicated Tool in the Study of Geodesy and Cartography”.EDULEARN15 Proceedings - 7th International Conference on Education and New Learning Technologies, Barcelona, Spain.ISBN978-84-606-8243-1.

Spoljašnje veze

KlatnonaWikimedijinoj ostavi

• Mathworld article on Mathieu Function
• Pendulum calculator
• Rubin, Julian (2007).„The Invention of the Foucault Pendulum”.Following the Path of Discovery, 2007, retrieved 2007-10-31. Directions for repeating Foucault's experiment, on amateur science site.
• Tobin, William.„The Life and Science of Léon Foucault”.Arhivirano izoriginalana datum 2018-09-12.Pristupljeno 2020-09-18.
• Bowley, Roger (2010).„Foucault's Pendulum”.Brady HaranforUniversity of Nottingham.