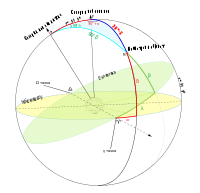
Nebeski koordinatni sistemi

2—centarMliječne staze
3—galaktički ekvator
4—sjeverni galaktički pol
6—ekliptika
7—sjeverni pol ekliptike
9—nebeski ekvator
10—sjeverni nebeski pol
11—γ-točka(točka proljetnogekvinocija)
12—Ω-točka(točka jesenjegekvinocija)
Sunce(5) iZemlja(8) su prikazani da bi se uočilo njihovo kretanje, i nisu dati u mjerilu
Nebeski koordinatni sistemisukoordinatni sistemikoji se koriste za opisivanje položaja astronomskih objekata nanebeskoj sferi.Razvijen je veći broj nebeskih koordinatnih sistema, a koristi se uvijek onaj najpogodniji za opisivanje datog objekta ili pojave.[1]Ovi koordinatni sistemi se po pravilu zasnivaju nasfernom koordinatnom sistemu,a međusobno se razlikuju po koordinatnom početku i pravcima u kojima su usmjerene osi. Prema položaju koordinatnog početka se mogu podjeliti na:[2]
- topocentrične— s centrom u promatraču,
- geocentrične— s centrom u centruZemlje,
- selenocentrične— s centrom u centruMjeseca,
- planetocentrične— s centrom u nekoj odplaneta(mora biti određena pri definiranju koordinatnog sistema),
- heliocentrične— s centrom u centruSuncai
- baricentrične— s centrom ucentru maseSunčevog sistema.
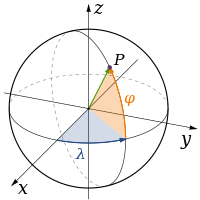
Sferni koordinatni sistem je definiran koordinatnim početkom i pravcima ka kojima su usmjerene osi. Ravan xy se naziva osnovna ravan. Sferne koordinate su udaljenost od koordinatnog početka (rili ρ), kut između pozitivnog smjerax-osi i projekcije promatrane točke na osnovnu ravan (longituda, na slici obilježena sa λ, u literaturi se upotrebljavaju i θ i φ), kao i kut između promatrane točke i osnovne ravni (latituda, na slici φ, može biti obilježena i sa β ili θ). U matematici se umjesto kuta između točke i osnovne ravni često koristi njemu komplementaran kut — kut između točke iz-osi (kolatituda). Ako je udaljenost od koordinatnog početka fiksna (kod nebeskih koordinatnih sistema se smatra da je beskonačna, v.nebeska sfera), za opis položaja su dovoljne dvije kutne koordinate.[2][3]

Iz perspektive promatrača, najprirodniji koordinatni sistem jehorizontski koordinatni sistem.Koordinatni početak je u promatraču, a osnovna ravan jehorizont,odnosno ravan tangentna naZemljuu točki u kojoj se nalazi posmatrač. Točka direktno iznad promatrača se nazivazenit,dok je njena antipodna tačkanadir.Koordinate suhorizontska visinaiazimut.Horizontska visina (a) je kut između promatranog objekta i ravni horizonta. Nekada se umjesto horizontske visine koristizenitna daljina(z), koja je komplementarna horizontskoj visini[4]:
Azimut (A) je kut između odabranog smjera i projekcije promatranog objekta na ravan horizonta. Azimut se može mjeriti od smjerasjeverailijuga,i to ili u smjeru kazaljke na satu (retrogradan, matematički negativan smjer) od 0° do 360°, ili na oba smjera od 0° do 180°, zbog čega je pri interpretaciji horizontskih koordinata potrebno obratiti pažnju kako je autor definirao azimut.[1][2][4].U ovom članku, azimut se mjeri od sjevera u smjeru kazaljke na satu (sjever: A = 0°; istok: A = 90°; jug: A = 180°; zapad: A = 270°).
Veliki krug nanebeskoj sferikoji sadrži sjeverni i južninebeski polse nazivameridijani normalan je nanebeski ekvator,a može se shvatiti i kao projekcijaZemaljskog meridijanana nebesku sferu. Meridijan koji prolazi i krozzenitinadirje lokalni meridijan datog promatrača, a sadrži i sjevernu i južnu tačku horizonta tog promatrača.Sunceizvijezdeimaju najvišu horizontsku visinu (kulminiraju) kada prolaze kroz lokalni meridijan.[1][2]
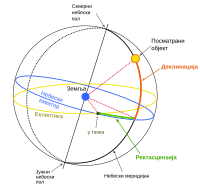
Druga prirodna osnovna ravan za promatrače na Zemlji je ravanekvatora.Kako prilikomrotacijeirevolucijeZemljesmjer Zemljine osi ostaje praktično nepromjenjen, tu se ne mijenja ni položaj ravni normalne na ovu os, a to je ravan ekvatora. Kut koji objekti zaklapaju sa ovom ravni se nazivadeklinacija.Deklinacija se obilježava slovom δ i izražava u stupnjevima; točke sjeverno od ekvatora imaju pozitivnu odnosno južno od ekvatora negativnu deklinaciju. Tako deklinacija sjevernognebeskog polaiznosi +90°, a južnog nebeskog pola -90°.[1][2][4]
S obzirom na činjenicu da jenebeski ekvatornagnut u odnosu na ravan Zemljine orbiteekliptike,postoje samo dvije presječne točke ovih ravni (promatrano kao dva velika kruga na nebeskoj sferi) —točka proljetnog(γ-točka) itočka jesenjeg ekvinocija(Ω-točka). Položaj γ-točke na nebeskoj sferi je relativno fiksan (uslijedprecesije,γ-točka napravi jedan pun krug po ekliptici za oko 25.800 godina), tako da je ona pogodna polazna tačka za mjerenje kuta na ekvatoru i na ekliptici. Kut između γ-točke i projekcije objekta na ravan nebeskog ekvatora mjeren u direktnom smjeru (matematički pozitivan smjer; suprotan kretanju kazaljke na satu) se nazivarektascenzijai obilježava se slovom α. Referentni sistem čije su koordinate rektascenzija i deklinacija se nazivanebeski ekvatorijalni koordinatni sistem,i najčešće je korišten nebeski koordinatni sistem za određivanje položaja tijela van Sunčevog sistema (katalozi zvijezda i objekata dubokog neba), jer se koordinate ovih tijela vrlo malo mjenjaju u nebeskom ekvatorijalnom koordinatnom sistemu (samo prilikom precesije i vlastitog kretanja, a diurnalno i godišnje kretanje Zemlje nema utjecaja). Rektascenzija se može izražavati u kutnim stupnjevima, minutima i sekundama, ili u satima, vremenskim minutima i vremenskim sekundama (1 sat odgovara uglu od 15°, s obzirom na to da Zemlja napravi pun krug tj. 360° za 24 sata).[1][2][4]

Umjesto smjera γ-točke, kao referentan smjer se može odabrati lokalni jug, odnosno lokalni meridijan. Kut mjeren od juga ka promatranom objektu u smjeru kazaljke na satu se nazivasatni kut(h), i pokazuje koliko je vremena prošlo od kako se objekt nalazio u lokalnom meridijanu. Deklinacija i satni kut su koordinatemjesnog ekvatorijalnog koordinatnog sistema.Satni kut γ-točke je lokalnozvjezdano (sideričko) vrijeme(θ). Važi odnos[4]
Sideričko vrijeme i satni kut se češće izražavaju u satima, vremenskim minutima i vremenskim sekundama nego u kutnim mjerama.[2]Svi objekti koji imaju istu rektascenziju imaju i isti satni kut, zbog čega se polukružnica definirana fiksnom rektascenzijom naziva isatna kružnica.Uzimajući ovu definiciju u obzir, može se reći da je satni kut onaj između lokalnog meridijana i satne kružnice.[1]
Položajzvijezdai drugihnebeskih tijelavanSunčevog sistemase po pravilu daje u odnosu nanebeski ekvatorijalni koordinatni sistem.Međutim, s obzirom na perturbacije kojeZemljatrpi na svojoj orbiti (precesija,nutacija,perturbacija putanje pod utjecajem drugih planeta), elementi koordinatnog sistema moraju biti jednoznačno definirani. U tu svrhu se definira odgovarajuća „epoha“,kako bi se znalo na koji trenutak se odnose koordinate (ekvatorijalne i ekliptičke). Trenutno je u upotrebi epoha J2000.0 (1. 1.2000.u 12:00UTC+0), zasnovana naFundamentalnom katalogu 5koji je objavljen1988.godine i sadrži referentne podatke za 3117fundamentalnih zvijezda.[1]
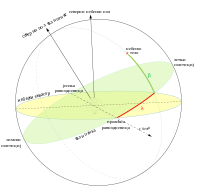

Ekliptika— ravanZemljineorbite ili veliki krug na nebeskoj sferi definiran godišnjim kretanjemSunca— osnovna je ravan još jednog važnog koordinatnog sistema, po njoj nazvanogekliptički koordinatni sistem.Postoje tri verzije u zavisnosti od položaja koordinatnog početka: topocentrična, geocentrična i heliocentrična. Za udaljene objekte, razlika među njima je zanemarljiva, ali ne i u slučaju tijelaSunčevog sistema.[4]
Pored kuta između objekta i ekliptike (ekliptička latituda, β), drugi kut je ekliptička longituda (λ) — kut između projekcije objekta na ravan ekliptike iγ-točke,koja je pogodna jer je dijele ekliptika inebeski ekvator.Ekliptička latituda je pozitivna sjeverno od ekliptike, a negativna južno od ekliptike. Sjeverni i južni ekliptički pol imaju latitudu +90° i -90°, respektivno. Sjeverni i južni nebeski pol, uslijedprecesije,kruže oko sjevernog i južnog pola ekliptike.[1][4]
Heliocentrična ekliptička latitutda i longituda se obilježavaju sa β’ i λ’, a za prevođenje iz geocentričnih u heliocentrične ekliptičke koordinate je potrebno znati i udaljenost do promatranog objekta. Konverzija se onda najlakše radi prevođenjem koordinata objekta uDekartove koordinate,preračunavanjem koordinata u odnosu na novi koordinatni početak (sve osi ostaju paralelne) i zatim preračunavanjem koordinata iz pravokutnih u nove sferne.[4]
Ekliptički koordinatni sistem je naročito pogodan za predstavljanje položaja tijela Sunčevog sistema, jerplanete(i njihovisateliti) malo odstupaju od ravni ekliptike, tako da uvijek imaju malu latitudu. Geocentrična ekliptička latituda Sunca i heliocentrična ekliptička latituda Zemlje su praktično nula.[4]

Galaktički koordinatni sistemje heliocentrični nebeski koordinatni sistem čija je osnovna ravan onaMliječne staze.S obzirom da Sunce leži vrlo blizu galaktičkoj ravni, bilo je moguće smjestiti centar ovog koordinatnog sistema u centar Sunca. Koordinate su galaktička latituda (b,pozitivna na sjever, negativna na jug) i galaktička longituda (l). Galaktička longituda se mjeri u direktnom smjeru od središta Mliječne staze, za koje se smatracrna rupa,koja predstavlja snažan izvorradio-zračenjai označava seSagittarius A*.Sagittarius A* dakle ima galaktičke koordinate l = 0° odnosno b = 0°, dok su njegove ekvatorijalne koordinate α = 17h45,7min,δ = -29° 00’. Ekliptičke koordinate galaktičkog sjevernog pola su α = 12h51,4min,δ = +27° 08’.[4]
Ovakav referentni sistem jeMeđunarodna astronomska unijadefinirala tek1959.godine, nakon što je utvrđen položaj središta galaksije. Prije toga je galaktička longituda računata od presjeka nebeskog ekvatora sa ravni galaksije. Danas se za galaktičke koordinate po starom sistemu koriste oznakelIibI.[4]
Relativnu planarnu distribucijumaglinauočio je jošWilliam Herschel,aGérard de Vaucouleursje sredinom20. vijekapotvrdio proučavanjem kataloga, postojanje supergalaktičke ravni, u čijoj blizini leži većina grupa galaksija i galaktičkih klastera koje pripadaju lokalnom superklasteruDjevici.Supergalaktički sjeverni pol ima galaktičke koordinatel= 47,37°,b= + 6,32°, a osnovni pravac je definiran presjekom sa ravni galaksije i ima koordinate 'l= 137,37°,b= 0°.[6]
S obzirom na to da katalozi objekata vanSunčevog sistema(zvijezde,maglice,galaksije...) najčešće koristeekvatorijalne koordinate,po pravilu se transformacije nebeskih koordinata vrše preko ekvatorijalnih koordinata. U daljem tekstu se koriste sljedeće oznake:
- A —azimut(računat od sjevera)
- a —horizontska visina
- z —zenitna daljina(90° - a)
- φ —geografska širinapromatrača
- δ —deklinacija
- α —rektascenzija
- h —satni kut
- ε —nagib ekliptike(kut izmeđuekliptikeinebeskog ekvatora)
- λ —ekliptička longituda
- β —ekliptička latituda
- l —galaktička longituda
- b —galaktička latituda

Za izvođenje transformacija koordinata jednog nebeskog koordinatnog sistema u drugi, potrebno je poznavati dva teoremasferne trigonometrije— sinusni i kosinusni teorem.[4]
- Sinusni teorem za sferni trokut glasi da je u datom sfernom trokutu, odnos sinusa kutova i sinusa njima nasuprotnih stranica konstantan:
- Kosinusni teorem sferne trigonometrije je:

Ako su date koordinate u horizontskom sistemu (visina a i azimut A), i ako je poznata geografska širina promatrača (φ), tada su odgovarajuće ekvatorske koordinate:[4]
Ako su poznate ekvatorske koordinate (satni kut t i deklinacija δ), kao i geografska širina promatrača, tada su odgovarajuće horizontske koordinate:[4]
Prve dvije jednadžbe iz oba seta ne smiju se dijeliti, jer bi se dobio tangnes satnog kuta (odnosno azimuta), a tangens kutova ne razlikuje kutove u prvom i trećem kvadrantu, odnosno u drugom i četvrtom kvadrantu.
Veza između rektascenzije (α) i satnog kuta je:
gdje je θ lokalnosideričko vrijeme.
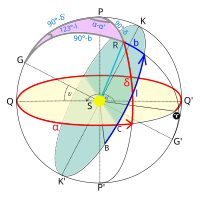
Ako su date deklinacija i rektascenzija nekog objekta, tada se njegove geocentrične ekliptičke koordinate mogu izračunati na sljedeći način:[4]
Obrnuto, ekvatorijalne koordinate se iz geocentričnih ekliptičkih mogu izračunati pomoću sljedećih jednadžbi:[4]
Neka je lNgalaktička longitudasjevernog nebeskog pola(123,0°), a αPi δPrektascenzijaideklinacijasjevernog galaktičkog pola (αP= 12h51,4min,δP= 27° 08’). Tada važe sljedeće relacije:[4]
- Sferni koordinatni sistem
- Sferna trigonometrija
- Geografske koordinate
- Precesija
- Nutacija
- Nagib ekliptike
- Sideričko (zvjezdano) vrijeme
- ↑1,01,11,21,31,41,51,61,7Patrick Moore, ur. (2002).Philip's Astronomy Encyclopedia.Philip's.ISBN0–540–07863–8.
- ↑2,02,12,22,32,42,52,6Paul Murdin, ur. (2001) ((en)).Encyclopedia of Astronomy and Astrophysics.Institure of Physics Publishing.ISBN0-7503-0440-5.
- ↑Tanton, James (2005).Encyclopedia of Mathematics.New York: Facts on File, Inc..ISBN0-8160-5124-0.
- ↑4,004,014,024,034,044,054,064,074,084,094,104,114,124,134,144,154,16Hannu Karttunen, Pekka Kröger, Heikki Oja, Markku Poutanen, Karl Johan Donner, ur. (2007) (en).Fundamental Astronomy(5th izd.). Berlin: Springer. str.21.ISBN978-3-540-34143-7.
- ↑Vondrák, J.; Capitaine, N.; Wallace, P. (2011-10-01).„New precession expressions, valid for long time intervals”(en).Astronomy & Astrophysics534:A22.DOI:10.1051/0004-6361/201117274.ISSN0004-6361.
- ↑O. Lahav; B. X. Santiago, A. M. Webster, Michael A. Strauss, M. Davis, A. Dressler and J. P. Huchra (2000).„The supergalactic plane revisited with the Optical Redshift Survey”.Mon. Not. R. Astron. Soc.(312): 166-176.
- Patrick Moore, ur. (2002).Philip's Astronomy Encyclopedia.Philip's.ISBN0–540–07863–8.
- Paul Murdin, ur. (2001) ((en)).Encyclopedia of Astronomy and Astrophysics.Institure of Physics Publishing.ISBN0-7503-0440-5.
- Tanton, James (2005).Encyclopedia of Mathematics.New York: Facts on File, Inc..ISBN0-8160-5124-0.
- Hannu Karttunen, Pekka Kröger, Heikki Oja, Markku Poutanen, Karl Johan Donner, ur. (2007) (en).Fundamental Astronomy(5th izd.). Berlin: Springer. str.21.ISBN978-3-540-34143-7.
- Positional AstronomyArhivirano2012-09-10 naWayback Machine-u— Sferna trigonometrija, nebeski koordinatni sistemi, transformacije koordinata, i prateći zadaci(en)
- Konverzija galaktičkih u druge nebeske koordinateArhivirano2016-03-04 naWayback Machine-u(en)
- Standardi funfamentalne astronomije (Međunarodna astronomska unija)— set algoritama i procedura koji implementiraju standardne modele koji se koriste u fundamentalnoj astronomiji (dostupan zaFortraniC)(en)
- Naval Observatory Vector Astrometry Software (NOVAS)Arhivirano2015-06-28 naWayback Machine-u— integrirani paket procedura za različite proračune u pozicijskoj astronomiji (dostupan zaFortran,CiPython)(en)























