Dot product

Inmathematics,thedot productis an operation that takes twovectorsas input, and that returns ascalarnumberas output. The number returned is dependent on the length of both vectors, and on theanglebetween them. The name is derived from thecentered dot"·" that is often used to designate this operation.Another name isscalar product.It emphasizes thescalar(rather thanvector) nature of the result.

Inthree-dimensional space,the dot product contrasts with thecross product,which produces a vector as result.

Definition

The dot product of two vectorsa= [a₁,a₂,...,a_n] andb= [b₁,b₂,...,b_n] is defined as:

$\mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}$

where Σ denotessummation notation(the sum of all the terms) andnis thedimensionof thevector space.

In dimension 2, the dot product of vectors [a,b] and [c,d] is ac + bd. The same way, in a dimension 3, the dot product of vectors [a,b,c] and [d,e,f] is ad + be + cf. For example, the dot product of two three-dimensional vectors [1, 3, −5] and [4, −2, −1] is

$[1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.$

Geometric interpretation

A•B= |A| |B| cos(θ).
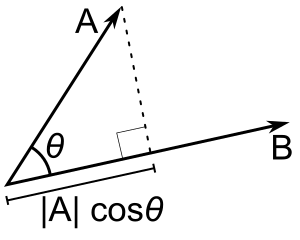
|A| cos(θ) is thescalar projectionofAontoB.

Vector Projection

The dot product of two vectorsaandbcan be interpreted as theproductof two lengths: the length ofaorthogonally projectedontob,and the length ofbitself. This can be written as$\|a\|\|b\|\cos(\theta )$,where θ (theta) is the angle between the two vectors. In the diagram shown,$\|a\|\cos(\theta )$is the length ofaorthogonally projected ontob,found usingtrigonometry.

The formula$\|a\|\|b\|\cos(\theta )$can be used to find certain properties.

$a\cdot a=\|a\|^{2}$

$\theta =\arccos({\frac {a\cdot b}{\left\|a\right\|\left\|b\right\|}})$

Rotation

Arotationof the orthonormal basis in terms of which vectorais represented is obtained with a multiplication ofaby arotation matrixR.Thismatrix multiplicationis just a compact representation of a sequence of dot products.

For instance, let

• B₁= {x,y,z} andB₂= {u,v,w} be two differentorthonormal basesof the same spaceR³,withB₂obtained by just rotatingB₁,
• a₁= (a_x,a_y,a_z) represent vectorain terms ofB₁,
• a₂= (a_u,a_v,a_w) represent the same vector in terms of the rotated basisB₂,
• u₁,v₁,w₁be the rotated basis vectorsu,v,wrepresented in terms ofB₁.

Then the rotation fromB₁toB₂is performed as follows:

${\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\\a_{v}\\a_{w}\end{bmatrix}}.$

Notice that the rotation matrixRis assembled by using the rotated basis vectorsu₁,v₁,w₁as its rows, and these vectors are unit vectors. By definition,Ra₁consists of a sequence of dot products between each of the three rows ofRand vectora₁.Each of these dot products determines a scalar component ofain the direction of a rotated basis vector (see previous section).

Ifa₁is arow vector,rather than acolumn vector,thenRmust contain the rotated basis vectors in its columns, and must post-multiplya₁:

${\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}.$

Physics

Inphysics,magnitude is ascalarin the physical sense, in that it is aphysical quantityindependent of the coordinate system, expressed as theproductof anumerical valueand aphysical unit,not just a number. The dot product is also a scalar in this sense, given by the formula, independent of the coordinate system. For example:

• Mechanical workis the dot product offorceanddisplacementvectors.
• Magnetic fluxis the dot product of themagnetic fieldand theareavectors.
• Volumetric flow rateis the dot product of the fluidvelocityand theareavectors.

Properties

The following properties hold ifa,b,andcare realvectorsandris ascalar.

The dot product iscommutative:

$\mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a}.$

The dot product isdistributiveover vector addition:

$\mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c}.$

The dot product isbilinear:

$\mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ).$

When multiplied by a scalar value, dot product satisfies:

$(c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )$

(these last two properties follow from the first two).

Two non-zero vectorsaandbareperpendicularif and only ifa•b= 0.

Unlike multiplication of ordinary numbers, where ifab=ac,thenbalways equalscunlessais zero, the dot product does not obey thecancellation law:

Ifa•b=a•canda≠0,then we can write:a• (b−c) = 0 by thedistributive law;the result above says this just means thatais perpendicular to (b−c), which still allows (b−c) ≠0,and thereforeb≠c.

Provided that the basis is orthonormal, the dot product is invariant under isometric changes of the basis: rotations, reflections, and combinations, keeping the origin fixed. The above mentioned geometric interpretation relies on this property. In other words, for an orthonormal space with any number of dimensions, the dot product is invariant under acoordinate transformationbased on anorthogonal matrix.This corresponds to the following two conditions:

• The new basis is again orthonormal (that is, orthonormal expressed in the old one).
• The new base vectors have the same length as the old ones (that is, unit length in terms of the old basis).

Ifaandbare functions, then the derivative ofa•bisa'•b+a•b'.

Triple product expansion

See the main article:Triple product

This is a very useful identity (also known asLagrange's formula) involving the dot- andcross-products.It is written as

$\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )$

which iseasier to rememberas "BAC minus CAB", keeping in mind which vectors are dotted together. This formula is commonly used to simplify vector calculations inphysics.

Proof of the geometric interpretation

Consider the element ofRⁿ

$\mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,$

Repeated application of thePythagorean theoremyields for its length |v|

$|\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,$

But this is the same as

$\mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,$

so we conclude that taking the dot product of a vectorvwith itself yields the squared length of the vector.

Lemma1

$\mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,$

Now consider two vectorsaandbextending from the origin, separated by an angle θ. A third vectorcmay be defined as

$\mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\ \mathbf {a} -\mathbf {b}.\,$

creating a triangle with sidesa,b,andc.According to thelaw of cosines,we have

$|\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta.\,$

Substituting dot products for the squared lengths according to Lemma 1, we get

$\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta.\,$(1)

But asc≡a−b,we also have

$\mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,$,

which, according to thedistributive law,expands to

$\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,$(2)

Merging the twoc•cequations,(1)and(2),we obtain

$\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta.\,$

Subtractinga•a+b•bfrom both sides and dividing by −2 leaves

$\mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta.\,$

Q.E.D.

Generalization

Theinner productgeneralizes the dot product toabstract vector spacesand is usually denoted by$\langle \mathbf {a} \,,\mathbf {b} \rangle$.Due to the geometric interpretation of the dot product, thenorm||a|| of a vectorain such aninner product spaceis defined as

$\|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}$

such that it generalizes length, and the angle θ between two vectorsaandbby

$\cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}.$

In particular, two vectors are consideredorthogonalif their inner product is zero

$\langle \mathbf {a} \,,\mathbf {b} \rangle =0.$

For vectors with complex entries, using the given definition of the dot product would lead to quite different geometric properties. For instance, the dot product of a vector with itself can be an arbitrary complex number, and can be zero without the vector being the zero vector; this in turn would have severe consequences for notions like length and angle. Many geometric properties can be salvaged, at the cost of giving up the symmetric and bilinear properties of the scalar product, by alternatively defining

$\mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}$

whereb_iis thecomplex conjugateofb_i.Then the scalar product of any vector with itself is a non-negative real number, and it is nonzero except for the zero vector. However, this scalar product is not linear inb(but ratherconjugate linear), and the scalar product is not symmetric either, since

$\mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}$.

This type of scalar product is nevertheless quite useful, and leads to the notions ofHermitian formand of generalinner product spaces.

TheFrobenius inner productgeneralizes the dot product to matrices. It is defined as the sum of the products of the corresponding components of two matrices having the same size.

Generalization to tensors

The dot product between atensorof order n and a tensor of order m is a tensor of order n+m-2. The dot product is worked out by multiplying and summing across a single index in both tensors. If$\mathbf {A}$and$\mathbf {B}$are two tensors with element representation$A_{ij\dots }^{k\ell \dots }$and$B_{mn\dots }^{p{\dots }i}$the elements of the dot product$\mathbf {A} \cdot \mathbf {B}$are given by

$A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}$

This definition naturally reduces to the standard vector dot product when applied to vectors, and matrix multiplication when applied to matrices.

Occasionally, a double dot product is used to represent multiplying and summing across two indices. The double dot product between two 2nd order tensors is a scalar.

Related pages

• Cauchy–Schwarz inequality
• Cross product
• Matrix multiplication

Other websites

• A quick geometrical derivation and interpretation of dot product
• Interactive GeoGebra Applet
• Java demonstration of dot product
• Another Java demonstration of dot product
• Explanation of dot product including with complex vectors
• "Dot Product"by Bruce Torrence,Wolfram Demonstrations Project,2007.
• Intuitive explanationvideo 1andvideo 2from onlineInteractive 3D graphics course