Fourierova vrsta

Prvi štirje približki Fourierovih vrst zapravokotni val.

Fourierove vrstevmatematikiomogočajo razstavljanje poljubneperiodične funkcijeali periodičnega signala v vsoto (po možnosti končno) skupine periodičnih funkcij kot stasinus in kosinus.Proučevanje Fourierovih vrst je vejaFourierove analize.

Tako se lahko na primer funkcijo$S(x)\!\,$razvije vneskončno vrstopo sinusih:

$S(x)=b_{1}\sin x+b_{2}\sin 2x+b_{3}\sin 3x+\cdots =\sum _{n=1}^{\infty }b_{n}\sin nx\!\,.$

Lahko pa se neko drugo funkcijo$C(x)\!\,$razvije v neskončno vrsto po kosinusih:

$C(x)=b_{0}+b_{1}\cos x+b_{2}\cos 2x+b_{3}\cos 3x+\cdots =b_{0}+\sum _{n=1}^{\infty }b_{n}\cos nx\!\,.$

Pri tem obe funkciji ohranita nekatere osnovne značilnosti, kot so periodičnost, lihost (ali sodost), vrednost pri$x=0\!\,$in$x=\pi \!\,$.

Imenujejo se po francoskem fiziku in matematikuJosephu Fourieru(1768–1830).

Definicija

Fourierov obrazec za periodične funkcije

Naj je periodična funkcija$f(x)\!\,$s periodo$2\pi \!\,$,ki jeintegrabilnanaintervalu$[-\pi,\pi ]\!\,$.Števila:

$a_{n}={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(x)\cos(nx)\,\mathrm {d} x,\quad n\geq 0\!\,$

in:

$b_{n}={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(x)\sin(nx)\,\mathrm {d} x,\quad n\geq 1\!\,$

se imenujejo Fourierovi koeficienti za funkcijo$f(x)\!\,$.

Včasih se uporablja tudi Fourierove vrste za$f\!\,$,ki se jih označuje z:

$(S_{N}f)(x)={\frac {a_{0}}{2}}+\sum _{n=1}^{N}\,[a_{n}\cos(nx)+b_{n}\sin(nx)],\quad N\geq 0\!\,.$

Delne vsote za$f\!\,$sotrigonometrični polinomi.Pričakuje se, da funkcije$S_{N}\!\,$za$f\!\,$dajejo približek, ki se približuje vrednosti za$f\!\,$,ko gre$N\!\,$proti neskončnosti. Neskončna vsota v obliki:

${\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\,[a_{n}\cos(nx)+b_{n}\sin(nx)]\!\,$

se imenuje Fourierova vrsta za$f\!\,$.

Fourierova vrsta nekonvergiravedno, saj se včasih celo za neko vrednost$x_{0}\!\,$vsota vrste v tej točki razlikuje od vrednosti$f(x_{0})\!\,$te funkcije.Harmonična analizaje področje, ki se ukvarja s konvergenco Fourierovih vrst. Kadar je kvadrat funkcije integrabilen naintervalu$[-\pi,\pi ]\!\,$,takrat Fourierova vrsta konvergira skoraj v vsaki točki. Predpostavi se lahko, da Fourierova vrsta konvergira v vsaki točki razen v točkah nezveznosti.

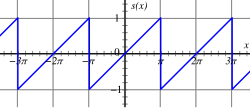
Zgled periodične funkcije, ki se imenuježagasti val.

Animacija prvih petih zaporednih delnih Fourierovih vrst.

Zgled

V zgledu se obravnavažagasti valin se ga razvije v Fourierovo vrsto. Žagasti val se opiše z naslednjo funkcijo:

$f(x)=x,\quad \mathrm {za} -\pi <x<\pi \!\,,$

$f(x+2\pi )=f(x),\quad \mathrm {za} -\infty <x<\infty \!\,.$

V tem primeru se dobi za Fourierove koeficiente:

${\begin{aligned}a_{0}&{}={\frac {1}{\pi }}\int _{-\pi }^{\pi }x\,\mathrm {d} x=0.\\a_{n}&{}={\frac {1}{\pi }}\int _{-\pi }^{\pi }x\cos(nx)\,\mathrm {d} x=0,\quad n\geq 0.\\b_{n}&{}={\frac {1}{\pi }}\int _{-\pi }^{\pi }x\sin(nx)\,\mathrm {d} x=-{\frac {2}{n}}\cos(n\pi )+{\frac {2}{\pi n^{2}}}\sin(n\pi )=2\,{\frac {(-1)^{n+1}}{n}},\quad n\geq 1.\end{aligned}}$

Lahko se dokaže, da Fourierova vrsta konvergira k vrednosti$f(x)\!\,$v vsaki točki, kjer je funkcija$f\!\,$diferenciabilna. Torej se lahko zapiše:

${\begin{aligned}f(x)&={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left(nx\right)+b_{n}\sin \left(nx\right)\right]\\&=2\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {za} \quad x-\pi \notin 2\pi Z.\end{aligned}}$

Eksponentna Fourierova vrsta

Uporabi seEulerjev obrazec,ki ima obliko:

$e^{inx}=\cos(nx)+i\sin(nx)\!\,,$

kjer je:

• $i\!\,$–imaginarna enota

S tem se dobi bolj zgoščeno obliko za Fourierovo vrsto:

$f(x)=\sum _{n=-\infty }^{\infty }c_{n}e^{inx}\!\,.$

Fourierovi koeficienti pa so:

$c_{n}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(x)e^{-inx}\,\mathrm {d} x\!\,.$

$a_{n}={c_{n}+c_{-n}}\quad {\text{ za }}n=0,1,2,\dots \!\,$

$b_{n}=i(c_{n}-c_{-n})\quad {\text{ za }}n=1,2,\dots \!\,$

in:

$c_{n}={\begin{cases}{\frac {1}{2}}(a_{n}-ib_{n})&n>0\\\quad {\frac {1}{2}}a_{0}&n=0\\{\frac {1}{2}}(a_{-n}+ib_{-n})&n<0\\\end{cases}}$

Zelo primerno je uporabiti obliko za$f\!\,$tako, da se dobi obrazec v obliki:

$f(x)=\sum _{n=-\infty }^{\infty }{\hat {f}}(n)\cdot e^{inx}\!\,.$

V tehniki se pogosto uporablja naslednjo obliko:

$f(x)=\sum _{n=-\infty }^{\infty }F[n]\cdot e^{inx}\!\,,$

kjer:

• $F[n]\!\,$pomeni, da je uporabljena nezveznadomena frekvenc.Zelo pogosto v tehniki spremenljivka$x\!\,$predstavljačas.

Fourierove vrste v splošnem intervalu

Obravnava se splošniinterval$[a,a+\tau ]\!\,$,kjer je s periodo$\tau \!\,$za vsa realna števila definirana funkcija$g(x)\!\,$s kompleksnimi koeficienti$G(n)\!\,$.Lahko se zapiše:

$g(x)=\sum _{n=-\infty }^{\infty }G[n]\cdot e^{i2\pi {\frac {n}{\tau }}x}\!\,.$

Če je funkcijakvadratno integrabilna(velja:$\int _{-\infty }^{\infty }|f(x)|^{2}\,\mathrm {d} x<\infty \!\,$), v intervalu$[a,a+\tau ]\!\,$,se jo lahko v tem intervalu prikaže z zgornjim obrazcem. To pa pomeni, da takrat, ko se dobi koeficiente za funkcijo$h(x)\!\,$z:

$G[n]={\frac {1}{\tau }}\int _{a}^{a+\tau }h(x)\cdot e^{-i2\pi {\frac {n}{\tau }}x}\,\mathrm {d} x\!\,,$

potem je$g(x)\!\,$povsod na intervalu$[a,a+\tau ]\!\,$enak$h(x)\!\,$.Iz tega sledi, da ima$h(x)\!\,$periodo enako$\tau \!\,$in, da naslednje

• sta$g(x)\!\,$in$h(x)\!\,$povsod enaka, razen na mestih nezveznosti
• $a\!\,$se lahko poljubno izbere. Najpogosteje se izbere$a=0\!\,$in$a=\tau /2\!\,$.

Fourierove vrste v kvadratu

Definira se lahko tudi Fourierove vrste za dve spremenljivkixinyv kvadratu$[-\pi,\pi ]\times [-\pi,\pi ]\!\,$:

$f(x,y)=\sum _{j,k\in \mathbb {Z} }c_{j,k}e^{ijx}e^{iky}\!\,,$

kjer je:

$c_{j,k}={1 \over 4\pi ^{2}}\int _{-\pi }^{\pi }\int _{-\pi }^{\pi }f(x,y)e^{-ijx}e^{-iky}\,\mathrm {d} x\,\mathrm {d} y\!\,.$

Hilbertov prostor

Če se obravnavaHilbertove prostore,množica funkcij$\{e_{n}=e^{inx},n\in \mathbb {Z} \}\!\,$tvoriortonormalno bazoprostora$L^{2}([-\pi,\pi ])\!\,$za kvadratno integrabilne funkcije v$[-\pi,\pi ]\!\,$.Ta prostor je Hilbertov prostor znotranjim produktomza poljubna dva elementa$f\!\,$in$g\!\,$,ki je definiran kot:

$\langle f,\,g\rangle \;{\stackrel {\mathrm {def} }{=}}\;{\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(x){\overline {g(x)}}\,\mathrm {d} x\!\,.$

Osnovne Fourierove vrste v Hilbertovih prostorih se lahko zapiše kot:

$f=\sum _{n=-\infty }^{\infty }\langle f,e_{n}\rangle \,e_{n}\!\,.$

To pa je enakovredno s kompleksno eksponentno obliko (glej zgoraj). Oblika s sinusom in kosinusom tvoriortogonalno množico:

$\int _{-\pi }^{\pi }\cos(mx)\,\cos(nx)\,\mathrm {d} x=\pi \delta _{mn},\quad m,n\geq 1,\!\,$

$\int _{-\pi }^{\pi }\sin(mx)\,\sin(nx)\,\mathrm {d} x=\pi \delta _{mn},\quad m,n\geq 1\!\,$

$\int _{-\pi }^{\pi }\cos(mx)\,\sin(nx)\,\mathrm {d} x=0\,\!\,,$

kjer je:

• $\delta _{mn}\!\,$–Kroneckerjeva delta.

Značilnosti

Funkcija$f\!\,$pripada$C^{k}(\mathbb {T} )\!\,$,če je$f\!\,$funkcija s periodo$2\pi \!\,$nad$\mathbb {R} \!\,$in, če je tak-krat odvedljiva in jek-ti odvod zvezen. Označi sen-ti Fourierov koeficient z${\widehat {f}}(n)\!\,$.

• če je$f\!\,$periodičnalihafunkcija,potem so$a_{n}=0\!\,$za vse$n\!\,$
• če je$f\!\,$periodičnasodafunkcija, potem so$b_{n}=0\!\,$za vse$n\!\,$
• če je$f\!\,$integrabilna funkcija velja$\lim _{|n|\rightarrow \infty }{\hat {f}}(n)=0\!\,$ter$\lim _{n\rightarrow +\infty }a_{n}=0\!\,$in$\lim _{n\rightarrow +\infty }b_{n}=0\!\,$.To jeRiemann-Lebesguov izrek
• dvojno neskončnozaporedje$\{a_{n}\}\!\,$v$c_{o}\!\,$je zaporedje Fourierovih koeficientov funkcije v$L^{1}[0,2\pi ]\!\,$,če in samo čeje tokonvolucijav$\ell ^{2}(\mathbb {Z} )\!\,$
• Parsevalov izrek:če je$f\in L^{2}([-\pi,\pi ])\!\,$,potem je tudi$\sum _{n=-\infty }^{\infty }|{\hat {f}}(n)|^{2}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }|f(x)|^{2}\,\mathrm {d} x\!\,$
• Plancherelov izrek:če so$c_{0},\,c_{\pm 1},\,c_{\pm 2},\ldots \!\,$koeficienti in velja$\sum _{n=-\infty }^{\infty }|c_{n}|^{2}<\infty \!\,$,potem obstaja funkcija$f\in L^{2}([-\pi,\pi ])\!\,$tako, da velja${\hat {f}}(n)=c_{n}\!\,$za vsak$n\!\,$
• prvikonvolucijski izrekpravi, da takrat, ko sta$f\!\,$in$g\!\,$vL¹([−π, π]), potem velja tudi${\widehat {f*g}}(n)=2\pi {\hat {f}}(n){\hat {g}}(n)\!\,$,kjer jeƒ∗gkonvolucija s periodo$2\pi \!\,$funkcij$f\!\,$in$g\!\,$
• drugi konvolucijski izrek pravi, da je${\widehat {f\cdot g}}={\hat {f}}*{\hat {g}}\!\,$.

Posplošitve

Obstaja več vrst posplošitev Fourierovih vrst. Njihovo proučevanje se imenuje harmonična analiza.

Približki in konvergenca Fourierovih vrst

Glej tudi:Gibbsov pojav

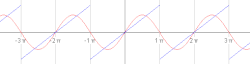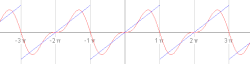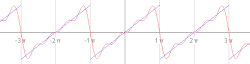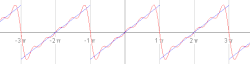
Gibbsov pojav

Približek reda 10 za pravokotni val.

Približek reda 50 za pravokotni val.

Približek reda 250 za pravokotni val.

Zelo pomembno vprašanje je povezano s konvergenco Fourierovih vrst. Pogosto je treba zamenjati neskončno vrsto$\sum _{-\infty }^{\infty }\!\,$s končno:$(S_{N}f)(x)=\sum _{n=-N}^{N}{\hat {f}}(n)e^{inx}\!\,$.Takšna vrsta se imenujedelna vsota.Želi se vedeti kako vrednost$(S_{N}f)(x)\!\,$konvergira k$f(x)\!\,$,ko gre$N\!\,$proti neskončnosti.

Divergenca Fourierovih vrst

Fourierove vrste so izredno dobro konvergentne. Vrste, ki bi bile divergentne so zelo redke. V letu 1922 je ruski matematikAndrej Nikolajevič Kolmogorov(1903–1987) v enem svojih del podal primer integrabilne funkcije, katere Fourierova vrsta je skoraj povsod divergentna.

Glej tudi

• Laurentova vrsta
• harmonična analiza
• spektralna teorija
• Fourierova transformacija
• Fejérov izrek
• Dichletovo jedro

Zunanje povezave

• Fourierova vrstaArhivirano2013-08-01 naWayback Machine.(slovensko)
• Fourierova vrsta na e-študijArhivirano2012-03-18 naWayback Machine.(slovensko)
• Weisstein, Eric Wolfgang.»Fourier Series«.MathWorld.
• Apleti za prikaz Fourierovih vrst(angleško)
• Fourierove vrste(angleško)
• Učbenik(angleško)
• Maths Online(angleško)
• Fourierove vrste in Fourierovi integrali(angleško)