Фрактал

Манделбротов скупје чувени пример фрактала.

Змајева крива

Фракталје „геометријски ликкоји се може разложити на мање делове тако да је сваки од њих, макар приближно, умањена копија целине “.Још се каже да је такав лик сам себи сличан. Термин је извеоБеноа Манделброт1975.године излатинскеречиfractusкоја има значење „сломљен “, „разломљен “.

Фрактал често има следеће особине:

• фину структуру на произвољно малом увећању;
• превише је неправилан да би могао бити описан традиционалнимеуклидским језиком;
• сам је себи сличан (макар приближно или стохастично);
• Хауздорфову димензијукоја је већа од његоветополошке димензије(иако овај услов не испуњавајубесконачно густе кривекао што јеХилбертова крива);
• једноставну ирекурзивну дефиницију.

Пошто се чине сличним на свим нивоима увећања, фрактали се често сматрају бесконачно комплексним у неформалном смислу речи. Природни облици који апроксимирају фрактале до извесне границе суоблаци,планински венци,муње,морске обале, и снежне пахуљице. Међутим, нису сви објекти који су сами себи слични истовремено и фрактали – пример јереална правакоја је формално сама себи слична, али не поседује остале особине фрактала.

Историја

Анимирана конструкцијатроугла Сјерпињског.

Математикакоја се налази у основи фрактала почела је да поприма свој облик у17. векукада је математичар и филозофЛајбницразматрао особинурекурзивнесличности самом себи, иако је он, грешком, сматрао да је само права линија слична самој себи у том смислу. Тек1872.године појављује се прва функција чији бисмо график данас сматрали фракталом, када јеКарл Вајерштрасдефинисаофункцијукоја је имала неинтуитивну особину да је на целој области дефинисаности биланепрекидна,али да ни у једној тачки није биладиференцијабилна.Три деценије касније,1904.годинеХелг Кох,незадовољан Вајерштрасовом превише апстрактном и аналитичком дефиницијом, у свом радуО једној непрекидној кривој без тангенти, добијеној помоћу елементарне геометријске конструкције(Sur une courbe continue sans tangente, obtenue par une construction geometrique elementaire) објављеном у часопису Arkivfor Matematikдаје геометријски дефиницију криве која је данас позната каоКохова пахуљица.1915.годинеВацлав Сјерпињскије конструисао својтроугао,а годину дана касније итепих Сјерпињског.У оригиналу, сви тигеометријски фракталису били описани као криве, а не као дводимензионални облици, како се третирају у модерним дефиницијама. Идеју о кривама које су сличне саме себи је даље развиоПол Пјер Леви,који је1938.године у свом радуРаванске или просторне криве и површи које су састављене од делова сличних целини(Plane or Space Curves and Surfaces Consisting of Parts Similar to the Whole) описао нову фракталну криву, познату данас каоЛевијева Ц крива.

ИГеорг Канторје, у периоду 1879—1884, када је објављивао серију од шест чланака који су заједно били увод у његовутеорију скупова,разматрао примере подскупова реалне праве са неуобичајеним особинама. ТиКанторови скуповису данас сврстани у фрактале.

Пред крај19.и почетком20. векаАнри Поенкаре,Феликс Клајн,Пјер ФатуиГастон Жулијасу истраживали итерирајуће функције укомплексној равни.Међутим без помоћи графике савременихрачунара,нису имали могућност визуелизације лепоте већине објеката које су открили.

Беноа Манделбротје шездесетих година 20. века почео да се бави самосличношћу у својим радовима као што је чланакКолико је дугачка британска обала? Статистичка самосличност и разломљене димезије(How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension), заснован на једном ранијем делу које је објавиоЛуис Фрај Ричардсон.

Напокон,1975.године, Манделброт је употребио реч „фрактал “да њоме означи објекат који је имао особину да му јеХауздорфова димензијавећа одтополошке.Ту математичку дефиницију је илустровао задивљујућом визуелизацијом добијеном помоћу рачунара. Већина генерисаних слика била је заснована нарекурзији,и тиме одредила општеприхваћено значење речи „фрактал “.

Области појављивања и примене фрактала

Фрактали се често појављују каоатракторидинамичких система,чак и у ситуацијама које се чине прилично једноставним (нпр.Жулијин скуп). Укомпјутерској графици,фрактали се користе за генерисање слика које представљају природне објекте:облаке,снег, морске обале, планинске венце, хрпе отпада...

Класификација фрактала

Према основној подели разликују се

• геометријски,
• алгебарскии
• стохастичнифрактали.

Поред тога, фрактали се, према постанку, могу поделити наприроднеивештачке,где се под вештачким фракталима подразумевају они до којих су дошли научници, а који, при произвољном увећању, задржавају особине фрактала. Код природних фрактала се јавља ограниченост области егзистенције - постоје максимална и минимална величина размере објекта за коју он поседује фракталне особине.

Полазни Манделбротов скуп	Увећање шест пута	Увећање 100 пута	Фини детаљи подсећају на полазни скуп

Фрактали се још деле на

• детерминисане(овде спадају геометријски и алгебарски фрактали) и
• недетерминисане(стохастичне фрактале).

У односу на степен самосличности, фрактали могу бити:

• потпуно самослични- највећи степен самосличности. Фрактал је идентичан самом себи на произвољном нивоу увећања. Ову особину имају фрактали кој се добијају помоћуитеративних функција.
• скоро самослични- мање строг облик самосличности; фрактал делује приближно (али не и потпуно) идентичан самом себи на различитим нивоима увећања. Овакве фрактале чине умањене копије целог фрактала у изобличеним и дегенерисаним облицима. Обично су то фрактали који се добијају помоћурекурентних веза.
• статистички самослични- најнижи ниво самосличности. Фрактал поседује нумеричке илистатистичкемере које се чувају кроз увећање или умањење. Најједноставније дефиниције фрактала тривијално указују на неку врсту статистичке самосличности (фрактална димензија је сама по себи нумеричка величина која се не мења са увећањем, односно умањењем). Овде спадају фрактали генерисани стохастичким процесима.

Геометријски фрактали

Менгеров сунђер

Канторов облак

Геометријски фракталису први фрактали које су изучавалиматематичариу19. веку,захваљујући њиховој очигледности, односно зато што је код њих одмах приметна особина самосличности.

Дводимензионегеометријске фрактале је могуће добити задавањем произвољнекривекоја ће послужити каогенератор.Затим се, у сваком следећем кораку, средњи део те криве замени генератором - умањеним ликом целе криве.Бесконачнимпонављањем овог поступка добија се изломљена фрактална крива. Иако је та крива веома сложена, њен општи облик могуће је задати само генератором. На тај начин могу се генерисатизмајева крива,Кохова крива,Левијева крива,крива Минковског,Пеанова криваиХилбертова крива.

Поред наведених фракталних кривих, у геометријске фрактале спадају иКанторов скуп,као и његова вишедимензиона уопштења, Канторова прашина (у равни) и Канторов облак (у простору),троугао Сјерпињског,тепих Сјерпињског,Питагорино дрвоиМенгеров сунђер.

Бесконачно густе криве

Бесконачно густе кривесу фракталне криве које након бесконачног броја итерација потпуно прекривају део$n$-димензионогпросторау којем се налазе ($n>1$). Тако ће бесконачно густа крива уравнизаузимати сваку тачку нпр.квадрата,а у тродимензионом простору сваку тачкукоцке.Први их је описао италијански математичарЂузепе Пеано,па се све оне понекад називају Пеановим кривама.

Својства

Фракталне димензијесвих бесконачно густих кривих одговарају тополошкој димензији простора у којем се налазе, баш зато што испуњавају читав тај простор, иако је њихова тополошка димензија увек$1$.Дакле, фрактална димензија бесконачно густих кривих уравни(јединичном квадрату) је$2$,упростору(јединичној коцки) је$3$итд.

Пеанова крива

Пеанова криваје прва описана бесконачно густа крива. Њу је1890.године описао италијански математичар Ђузепе Пеано.

Конструкција

Пеанова крива се конструише низомитерација.Прва итерација је задата каква јесте. Наредну итерацију добијамо на следећи начин:

• Претходну итерацију посматрамо као квадрат и поделимо га на 9 нових квадрата једнаких величина.
• Сваки од тих квадрата заменимо 9 пута умањеним квадратом из претходне итерације.
• Затим се изврши хоризонтална, односно вертикалнарефлексијаквадрата, како би спајање било коректно извршено.
• На крају, криве у квадратима се споје у једну непрекидну криву.

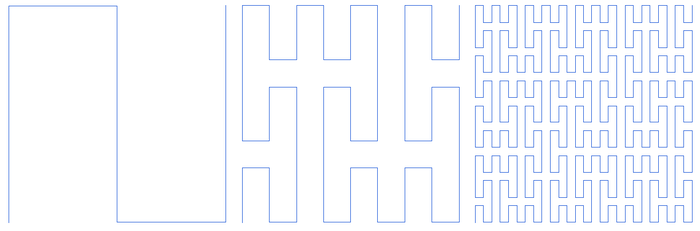Прве три итерације Пеанове криве

Постоји велики број варијанти Пеанових кривих, у зависности изгледа прве итерације и поделе на квадрате.

Хилбертова крива

Анимирана конструкција Хилбертове криве у првих 8 итерација

При конструкцији Хилбертове криве користи се идеја базирана на подели квадрата на 4 мања, уместо на 9 мањих квадрата једнаких величина.

Хилбертова криваје бесконачно густа крива коју је описаонемачкиматематичарДавид Хилберт1891.године.

Хауздорфова димензија Хилбертове криве је$2$.Иако је Хилбертова крива у равни ограничена квадратом, њена дужина експоненцијално расте са бројем итерација и износи$H_{n}=2^{n}-{\frac {1}{2^{n}}}$.

Конструкција

Конструкција је слична конструкцији Пеанове криве. Прво, задају се две почетне итерације (онакве какве јесу), а затим се у свакој наредној итерацији сви сегменти слични кривој из прве итерације замене читавом кривом из друге итерације. Даља конструкција се може извршити на два начина, иако је резултат потпуно исти:

• $n$-ту итерацију добијемо ако у$(n-1)$-ој итерацији сваки сегмент сличан кривој из прве итерације заменимо читавомдругомитерацијом.
• $n$-ту итерацију добијемо ако у$(n-1)$-ој итерацији сваки сегмент сличан кривој из претходне итерације заменимотомчитавом итерацијом.

Прва итерација	Прва и друга итерација	Прве три итерације

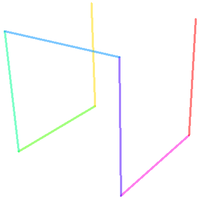
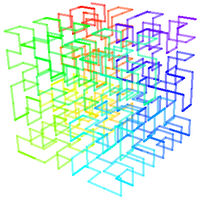
Хилбертова крива у простору се прави једноставном аналогијом.

Прва итерација

Друга итерација

Трећа итерација

Четврта итерација

Конструкција коришћењем L-система

• Почетак:$L$
• Правила:
  • $L$→$+RF-LFL-FR+$
  • $R$→$-LF+RFR+FL-$
• Значење:
  • $F$$=$"цртај напред"
  • $-$$=$"окрени у смеру казаљке на сату за${\frac {\pi }{2}}$"
  • $+$$=$"окрени у смеру супротном од смера казаљке на сату за${\frac {\pi }{2}}$"

Примене

Хилбертова крива има вишеструке примене у разним областима, а највише у рачунарству и информатици. Користи се код IP адреса рачунара, како би могла да се конструише слика мреже. Код за генерисање слике ће претворити 2D у 1D да би нашао боју сваког пиксела, а Хилбертова крива се понекад користи јер блиске IP адресе у слици чува једну близу друге. Такође је нашла примену у мултидимензионим базама података - при тражењу записа могу помоћи у одређивању приоритета претраге. Користе се и при изради црно-белих фотографија. Хилбертове криве у већим димензијама представљају генерализацијуГрејевог кода,и користе се у сличне сврхе.

Алгебарски фрактали

Алгебарски фракталису они фрактали за чију се конструкцију користе итеративне нелинеарнефункцијекојесе задају једноставним алгебарскимформулама.

Нуле функције трећег степена у комплексној равни * све тачке исте боје конвергирају ка једном решењу

У16. векуиталијански математичари су развили егзактне формуле за решавање алгебарскихједначинатрећег и четвртог степена, а почетком19. векаматематичарНилс Абелдоказао је да не постоје универзалне методе којима би се решавале једначине петог и вишег степена. Но, такве се једначине могу решаватиприближно,до потребне тачности. Методе приближног решавања једначина развијале су се током више векова.Исак Њутнје развио специифчну итеративну методу коју је касније усавршиоЏозеф Рафсон.

Апроксимација функција

$f(x)={\frac {x^{2}}{4}}$

$f(x)=\sin x$

Претпоставимо да нула непрекидне функције припадаинтервалу$[A,B]$.Одаберемо једну од крајњих тачака интервала, на пример$A$,и одредимо тангенту у њој. Означимо тачку пресека$A'$тангенте и апсцисе и поступак поновимо примењен на интервал$[A',B]$.Поступак поноваљамо све док не постигнемо задовољавајућу тачност решења, односно док посматрани интервал не постане довољно мали.

Треба приметити да у случајевима са слика са стране приближна решења постају све ближа стварном решењу, односно конвергирају му, иако су код леве функције "суседна" приближна решења увек са супротне стране стварног.

Ова метода може се применити и накомплекснураван. Размотримо нуле комплексне функције$p(z)=z^{3}-1$.

Из графика са стране видимо да су границе три скупа сложене те да даљим повећавањем добијамо све већу сложеност. Осим тога, гранична подручја садрже подручја која су потпуно слична подручјима у којима се налазе. Другим речима, она поседују својство самосличности, односно то суфрактали.

Жулијин скуп

Жулијин скуп

Жулијин скуп (у ширем смислу)је границаскуповатачака$z_{0}=x+iy$у којима низ${\mathit {z}}_{n+1}=f(z_{n})$конвергира и скупа тачака за које тај низ дивергира. Овде$f(z_{n})$може бити било kојафункција.

Жулијин скуп (у ужем смислу)добијамо ако за функцију$f(z_{n})$изаберемо$f(z_{n})=z_{n}^{2}+c$.

Добио је име пофранцускомматематичаруГастону Жулији.

Конструкција

Ако се за сваку тачку комплексне равни$z_{0}=x+iy$дефинише низ${\mathit {z}}_{n+1}=f(z_{n})$,где је$f(z_{n})$може бити било која функција, можемо дефинисати два скупа:скуп тачака$z_{0}$за које дефинисани низ конвергира и скуп тачака$z_{0}$за које тај низ дивергира, односно тежи у бесконачност.Жулијин скуп (у ширем смислу) је граница тих скупова. Обично се Жулијин скуп, као и сви алгебраски фрактали, приказује тако да су тачке које конвергирају црне, а оне које дивергирају у разним нијансама исте или различитих боја. Нијанса боје зависи од брзине којом низ расте – што се више одмичемо од Жулијиног скупа, низ брже расте. Мењањем константе$c$у Жулијином скупу у ужем смислу добијамо најразличитије скупове.

Повезаност

Жулијин скуп је повезан ако је скуп који окружујекомпактан..Ова је особина врло важна за дефиницијуМанделбротовог скупа.

• 
  c=1-φ, φ =zlatni rez
  (повезан)
• 
  c=(φ-2)+(φ-1)i = -0.4+0.6i
  (неповезан)
• 
  c=0.285+0i
  (неповезан)
• 
  c=0.285+0.01i
  (неповезан)
• 
  c=0.45+0.1428i
  (неповезан)
• 
  c=-0.70176-0.3842i
  (повезан)

Манделбротов скуп

Манделбротов скупу комплексној равни

Манделбротов скуп је најсавршенији од свих фрактала. Одређен је рекурентном функцијом$z_{n+1}=z_{n^{2}}+c$,где је$c$комплексан број такав да је Жулијин скуп повезан.

Тачније, Манделбротов скуп је скуп свих комплексних бројева$c$таквих да је, за почетни услов$z_{0}=0$,модуо комплексног броја$z_{n+1}=z_{n^{2}}+c$ограничен.

Све тачке Манделбротовог скупа$M$леже унутар круга полупречника 2. Наиме:

$z_{0}=0,\quad z_{1}=c,\quad z_{2}=c^{2}+c,\ldots,z_{n+1}=z_{n^{2}}+c$

$c\in M\ \Longleftrightarrow \ \lim _{n\rightarrow \infty }|z_{n+1}|\leq 2$.

Разни самослични фрактали, којима припада и Манделбротов, најједноставније се конструишу уз помоћ"escape - time"алгоритма.

Псеудо код за цртање Манделбротовог скупа:

ulaz:sirinaivisinaekrana;
maksimalnibrojiteracijamax_iter;
niz[];

begin

fori:=0tovisinado
forj:=0tosirinado

Re_c=(j-sirina/2)*4/sirina;
Im_c=(i-visina/2)*4/sirina;

x=0;y=0;
iter=0;

whilex*x+y*y<=4anditer<max_iterdo
tmp=x*x-y*y+Re_c;
y=2*x*y+Im_c;
x=tmp;
iter++;

ifiter<max_iterthen
oboji_piksel(j,i,boja[iter]);
else
oboji_piksel(j,i,crno);

end

Горући брод

Горући брод је фрактал којег су описали Мајкл Микетлиш и Ото Рослер 1992. Конструише се на сличан начин као и Жулијин скуп: за сваку тачку комплексне равни$z_{0}=x_{0}+iy_{0}$одреди низ тачака$z_{n+1}=x_{n+1}+iy_{n+1}$tako da je$x_{n+1}=x_{n}^{2}-y_{n}^{2}-x_{0}$и$y_{n+1}=2|x_{n}y_{n}|-y_{0}$.Тачке које након много итерација конвергирају ка једној вредности припадају скупу, па се обоје једном бојом. Остале тачке дивергирају и обоје се различитим нијансама, зависно од тога колико брзо дивергирају.

Горући брод је скуп белих тачака

Увећан доњи леви део слике лево који показује самосличност фрактала

Њутнов фрактал

Њутнов фракталза полином седмог степена

Њутнова методаза налажење корена функције се базира на, такође, итеративном процесу. Њутнов фрактал је управо граница скупа у комплексној равни дефинисаног Њутновим методом примењеним на полином комплексног броја. Са Манделбротовим скупом, Њутнов метод је повезан на најневероватнији начин. Испитиван је Њутнов метод над одређеном кубном комплексном функцијом. На комплексној равни са три боје су обележаване тачке које би као почетне довеле до откривања корена једнаком$1$,тачке које би конвергирале ка неком од преостала два корена и тачке које су упадале у циклусе између бар два корена. Увеличавањем добијене слике откривен је фрактал Манделбротовог скупа, онако како га знамо за квадратну итеративну функцију, а припадао је области тачака које нису конвергирале ка само једном корену.

За неке веома једноставне физичке системе (механички, магнетни, оптички, итд.) показује се да су атракторске области коренова изразито фрактално разломљене и једноставни системи постају практично непредвидљиви. Њихово коначно стање драстично зависи од почетних услова и ово је прва назнака повезаности фрактала и хаоса.

Види још

• Систем итериране функције

Литература

• Peitgen, Heinz-Otto; Richter, Peter (1986).The Beauty of Fractals.Heidelberg: Springer-Verlag.ISBN978-0-387-15851-8.
• Mandelbrot, B.B. (1982).The Fractal Geometry of Nature.W.H. Freeman and Company.ISBN978-0-7167-1186-5.
• Edgar, Gerald (2008).Measure, Topology, and Fractal Geometry.New York: Springer Science+Business Media. стр. VII.ISBN978-0-387-74748-4.
• Falconer, Kenneth (1982).Fractal Geometry: Mathematical Foundations and Applications.John Wiley & Sons, Ltd.ISBN978-0-470-84862-3.
• Miroslav M. Novak, ур. (2004).Thinking in Patterns: Fractals and Related Phenomena in Nature.World Scientific Publishing Co. Pte. Ltd.ISBN978-981-238-822-3.

Спољашње везе

• Фракталина mathworld.wolfram.com(језик: енглески)
• Предавања о фракталимаса Универзитета Јејл(језик: енглески)
• Хаос и фрактали(језик: енглески)
• Особине фрактала(језик: енглески)
• Фрактали - чудесне слике хаоса(језик: хрватски)
• Фрактални облици у нумеричким апроксимацијама(језик: хрватски)