Sơ bài tự

Sơ bài tự
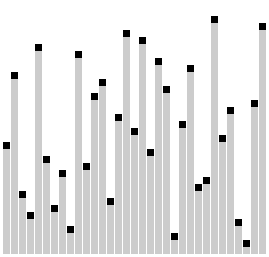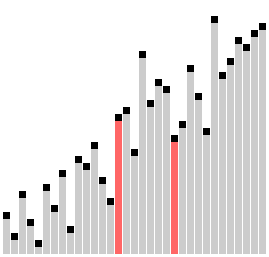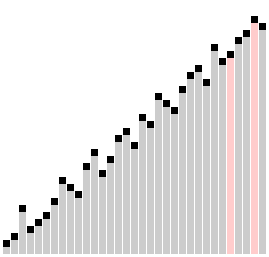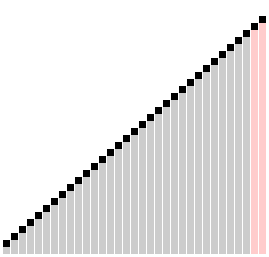Sử dụng sơ bài tự vi nhất liệt sổ tự tiến hành bài tự đích quá trình
Khái huống
Loại biệt	Bài tự toán pháp
Tư liêu kết cấu	Trận liệt
Phục tạp độ
Bình quân thời gian phục tạp độ	$\Omega (n^{2}/2^{p})$ Kỳ trungpBiểu kỳ tăng lượng (the number of increments)
Tối phôi thời gian phục tạp độ	$\Omega (n^{2})$
Tối ưu thời gian phục tạp độ	$O(n\log n)$
Không gian phục tạp độ	$O(1)$
Tương quan biến lượng đích định nghĩa

Sơ bài tự( anh ngữ:Comb sort) thị nhất chủng do phất lạp cơ mễ nhĩ · đa bác xá duy kỳ ( Wlodzimierz Dobosiewicz ) ô 1980 niên sở phát minh đích bất ổn địnhBài tự toán pháp,Tịnh do sử đế phân · lai tây ( Stephen Lacey ) hòa lý tra đức · bác khắc tư ( Richard Box ) ô 1991 niên tứ nguyệt hào đíchByte tạp chíTrung thôi quảng. Sơ bài tự thị cải lương tựPhao mạt bài tựHòaKhoái tốc bài tự,Kỳ yếu chỉ tại ô tiêu trừ “Ô quy”, diệc tức tại trận liệt vĩ bộ đích tiểu sổ trị, giá ta sổ trị thị tạo thành phao mạt bài tự hoãn mạn đích chủ nhân. Tương đối địa, “Thỏ tử”, diệc tức tại trận liệt tiền đoan đích đại sổ trị, bất ảnh hưởng phao mạt bài tự đích hiệu năng.

Tại phao mạt bài tự trung, chỉ bỉ giác trận liệt trung tương lân đích nhị hạng, tức bỉ giác đích nhị hạng đích gian cự ( Gap ) thị 1, sơ bài tự đề xuất thử gian cự kỳ thật khả đại ô 1, cải tựSáp nhập bài tựĐíchHi nhĩ bài tựĐồng dạng đề xuất tương đồng quan điểm. Sơ bài tự trung, khai thủy thời đích gian cự thiết định vi trận liệt trường độ, tịnh tại hồi quyển trung dĩ cố định bỉ suất đệ giảm, thông thường đệ giảm suất thiết định vi 1.3. Tại nhất thứ hồi quyển trung, sơ bài tự như đồng phao mạt bài tự nhất dạng bả trận liệt tòng thủ đáo vĩ tảo miêu nhất thứ, bỉ giác cập giao hoán lưỡng hạng, bất đồng đích thị lưỡng hạng đích gian cự bất cố định ô 1. Như quả gian cự đệ giảm chí 1, sơ bài tự giả định thâu nhập trận liệt đại trí bài tự hảo, tịnh dĩ phao mạt bài tự tác tối hậu kiểm tra cập tu chính.

Đệ giảm suất

Đệ giảm suất đích thiết định ảnh hưởng trứ sơ bài tự đích hiệu suất, nguyên tác giả dĩ tùy cơ sổ tác thật nghiệm, đắc đáo tối hữu hiệu đệ giảm suất vi 1.3 đích. Như quả thử bỉ suất thái tiểu, tắc đạo trí nhất hồi quyển trung hữu quá đa đích bỉ giác, như quả bỉ suất thái đại, tắc vị năng hữu hiệu tiêu trừ trận liệt trung đích ô quy.

Diệc hữu nhân đề nghị dụng$1/\left(1-{\frac {1}{e^{\varphi }}}\right)\approx 1.247330950103979$Tác đệ giảm suất, đồng thời tăng gia hoán toán biểu hiệp trợ ô mỗi nhất hồi quyển khai thủy thời kế toán tân gian cự.

Nhân vi trình thức ngữ ngôn trung thừa pháp bỉ trừ pháp khoái, cố hội thủ đệ giảm suất đảo sổ dữ gian cự tương thừa,${\frac {1}{1.247330950103979}}=0.801711847137793\approx 0.8$

Biến dị hình thức

Sơ bài tự -11

Thiết định đệ giảm suất vi 1.3 thời, tối hậu chỉ hội hữu tam chủng bất đồng đích gian cự tổ hợp: (9, 6, 4, 3, 2, 1), (10, 7, 5, 3, 2, 1), hoặc (11, 8, 6, 4, 3, 2, 1). Thật nghiệm chứng minh, như quả gian cự biến thành 9 hoặc 10 thời nhất luật cải tác 11, tắc đối hiệu suất hữu minh hiển cải thiện, nguyên nhân thị như quả gian cự tằng kinh thị 9 hoặc 10, tắc đáo gian cự biến thành 1 thời, sổ trị thông thường bất thị đệ tăng tự liệt, cố thử yếu tiến hành kỉ thứ phao mạt bài tự hồi quyển tu chính. Gia nhập thử chỉ định gian cự đích biến dị hình thức xưng viSơ bài tự -11(Combsort11).

Hỗn hợp sơ bài tự hòa kỳ tha bài tự toán pháp

Như đồngKhoái tốc bài tựHòaHợp tịnh bài tự,Sơ bài tự đích hiệu suất tại khai thủy thời tối giai, tiếp cận kết thúc thời tối soa. Như quả gian cự biến đắc thái tiểu thời ( lệ như tiểu ô 10), cải dụngSáp nhập bài tựHoặcHi nhĩ bài tựĐẳng toán pháp, khả đề thăng chỉnh thể hiệu năng.

Thử phương pháp tối đại hảo xử thị bất nhu yếu kiểm tra thị phủ tiến hành quá giao hoán trình tự dĩ tương bài tự hồi quyển đề tảo kết thúc.

Hư nghĩ mã

Sơ bài tự trình tự ( dĩ array tác thâu nhập )
gap = array đích trường độ// thiết định khai thủy thời đích gian cự


Đương gap > 1 hoặc swaps = 1 thời chấp hành hồi quyển// đại biểu vị hoàn thành bài tự
gap = thủ “gap trừ dĩ đệ giảm suất” đích chỉnh sổ trị// canh tân gian cự


swaps = 0// dụng dĩ kiểm tra trận liệt thị phủ dĩ tại đệ tăng hình thức, chỉ hạn gap=1 thời hữu hiệu


// bả thâu nhập trận liệt “Sơ” nhất thứ
i = 0 đáo (array đích trường độ - 1 - gap) lai chấp hành hồi quyển// tòng thủ đáo vĩ tảo miêu nhất thứ; nhân vi trận liệt nguyên tố đích biên hào tòng 0 khai thủy, sở dĩ tối hậu nhất cá nguyên tố biên hào vi trường độ -1
Như quả array[i] > array[i+gap]
Bả array[i] hòa array[i+gap] đích sổ trị giao hoán
swaps = 1// tằng tác giao hoán, cố thử trận liệt vị tất bài tự hảo
Như quả kết thúc
Hồi quyển kết thúc
Hồi quyển kết thúc
Trình tự kết thúc

Thật tác phạm lệ

C ngữ ngôn

voidcomb_sort(intarr[],intlen){
doubleshrink_factor=0.8;
intgap=len,swapped=1,i;
inttemp;
while(gap>1||swapped){
if(gap>1)
gap*=shrink_factor;
swapped=0;
for(i=0;gap+i<len;i++)
if(arr[i]>arr[i+gap]){
temp=arr[i];
arr[i]=arr[i+gap];
arr[i+gap]=temp;
swapped=1;
}
}
}

C++

template<typenameT>// chỉnh sổ hoặc phù điểm sổ giai khả sử dụng, nhược yếu sử dụng vật kiện ( class ) thời tất tu thiết định đại ô ( > ) đích vận toán tử công năng
voidcomb_sort(Tarr[],intlen){
doubleshrink_factor=0.8;
intgap=len,swapped=1,i;
while(gap>1||swapped){
if(gap>1)
gap=(int)((double)gap*shrink_factor);
swapped=0;
for(i=0;gap+i<len;i++)
if(arr[i]>arr[i+gap]){
swap(arr[i],arr[i+gap]);
swapped=1;
}
}
}

Java

publicstatic<EextendsComparable<?superE>>voidsort(E[]input){
intgap=input.length;
booleanswapped=true;
while(gap>1||swapped){
if(gap>1){
gap=(int)(gap*0.8);
}
inti=0;
swapped=false;
while(i+gap<input.length){
if(input[i].compareTo(input[i+gap])>0){
Et=input[i];
input[i]=input[i+gap];
input[i+gap]=t;
swapped=true;
}
i++;
}
}
}

JavaScript

Array.prototype.comb_sort=function(){
varshrink_factor=0.8;
vargap=this.length,swapped=1,i;
vartemp;
while(gap>1||swapped){
if(gap>1)
gap=Math.floor(gap*shrink_factor);
swapped=0;
for(i=0;gap+i<this.length;i++)
if(this[i]>this[i+gap]){
temp=this[i];
this[i]=this[i+gap];
this[i+gap]=temp;
swapped=1;
}
}
returnthis;
};

PHP

functionswap(&$x,&$y){
$t=$x;
$x=$y;
$y=$t;
}
functioncomb_sort(&$arr){//php đích trận liệt thị vi cơ bổn hình biệt, sở dĩ tất tu dụng truyện tham khảo tài năng tu cải nguyên trận liệt
$shrink_factor=0.8;
$gap=count($arr);
$swapped=1;
while($gap>1||$swapped){
if($gap>1)
$gap=floor($gap*$shrink_factor);
$swapped=0;
for($i=0;$gap+$i<count($arr);$i++)
if($arr[$i]>$arr[$i+$gap]){
swap($arr[$i],$arr[$i+$gap]);
$swapped=1;
}
}
}

Go

funccomb_sort(datasort.Interface){
n:=data.Len()
shrinkFactor:=0.8
gap:=n
swapped:=true

forgap>1||swapped{
ifgap>1{
gap=int(float64(gap)*shrinkFactor)
}

// mạo phao bài tự
swapped=false
fori:=0;i<n-gap;i++{
ifdata.Less(i+gap,i){
data.Swap(i+gap,i)
swapped=true
}
}
}
}

Julia ( trình thức ngữ ngôn )

# Julia Sample: CombSort

functionCombSort(A)
gap,swapped=length(A),1

while(gap>1)||(swapped==1)
gap=floor(Int,gap/1.25)
swapped=0
fori=1:(length(A)-gap)
ifA[i]>A[i+gap]
A[i],A[i+gap]=A[i+gap],A[i]
swapped=1
end
end
end
returnA
end

# Main Code
A=[16,586,1,31,354,43,3]
println(A)# Original Array
println(CombSort(A))# Comb Sort Array

Động tác nguyên lý

Giả thiết thâu nhập vi

8 4 3 7 6 5 2 1

Mục tiêu vi tương chi biến thành đệ tăng bài tự. Nhân vi thâu nhập trường độ =8, khai thủy thời thiết định gian cự vi 8/1.3≒6, tắc bỉ giác 8 hòa 2, 4 hòa 1, tịnh tác giao hoán lưỡng thứ.

84 3 7 6 521

243 7 6 5 81

2 1 3 7 6 5 8 4

Đệ nhị thứ hồi quyển, canh tân gian cự vi 6/1.3≒4. Bỉ giác 2 hòa 6, 1 hòa 5, trực chí 7 hòa 4, thử hồi quyển trung chỉ tu giao hoán nhất thứ.

2 1 376 5 84

2 1 3 4 6 5 8 7

Tiếp hạ lai đích mỗi thứ hồi quyển, gian cự y thứ đệ giảm vi 3 → 2 → 1,

Gian cự =3 thời, bất tu giao hoán

2 1 3 4 6 5 8 7

Gian cự =2 thời, bất tu giao hoán

2 1 3 4 6 5 8 7

Gian cự h=1 thời, giao hoán tam thứ

213 4 6 5 8 7

1 2 3 4658 7

1 2 3 4 5 687

1 2 3 4 5 6 7 8

Thượng lệ trung, cộng tác liễu lục thứ giao hoán dĩ hoàn thành bài tự.

Tham khán

• Phao mạt bài tự,Sơ bài tự đích cơ bổn, giác mạn đích toán pháp.
• Kê vĩ tửu bài tự,Hoặc song hướng phao mạt bài tự, nhất dạng giải quyết liễu phao mạt bài tự trung đích ô quy vấn đề.

Ngoại bộ liên kết

• .NET Implementation of comb sort and several other algorithms(Hiệt diện tồn đương bị phân,Tồn vuHỗ liên võng đương án quán)
• Combsort - Who ever knew that bubblesort could be so good?